4. Постановка задачи многокритериальной оптимизации
В более сложных ситуациях приходится иметь дело не с одной, а сразу с несколькими целевыми функциями. Так будет, например, когда какое-то явление, объект или процесс рассматривается с различных точек зрения и для формализации каждой точки зрения используется соответствующая функция. Если явление рассматривается в динамике, поэтапно и для оценки каждого этапа приходится вводить отдельную функцию, в этом случае также приходится учитывать несколько функциональных
показателей.
Нижеследующее рассмотрение посвящено
ситуации, когда имеется несколько
числовых функций
,
,
определенных на множестве
.
В зависимости от содержания задачи выбора эти функции называют критериями оптимальности, критериями эффективности, целевыми функциями, показателями или критериями качества.
Проиллюстрируем
введенные термины, рассмотрев
задачу выбора наилучшего проектного
решения. В
этой задаче множество
состоит из нескольких конкурсных
проектов (например, строительства нового
предприятия), а критериями оптимальности
могут служить стоимость реализации
проекта
и величина прибыли
,
которую обеспечит данное проектное
решение (т.е. построенное предприятие).
Если ограничить рассмотрение данной
задачи лишь одним критерием оптимальности,
практическая значимость решения такой
задачи окажется незначительной. В самом
деле, при использовании только первого
критерия будет выбран самый дешевый
проект, но его реализация может привести
к недопустимо малой прибыли. С другой
стороны, на строительство самого
прибыльного проекта, выбранного на
основе второго критерия оптимальности,
может просто не хватить имеющихся
средств. Поэтому в данной задаче
необходимо учитывать оба указанных
критерия одновременно. Если же
дополнительно стараться минимизировать
нежелательные экологические последствия
строительства и функционирования
предприятия, то к двум указанным следует
добавить еще один – третий критерий и
т.д. Что касается ЛПР, осуществляющего
выбор проекта, то в данной задаче таковым
является глава администрации района,
на территории которого будет построено
предприятие, при условии, что это
предприятие является государственным.
Если же предприятие – частное, то в
качестве ЛПР выступает глава соответствующей
фирмы.
Указанные выше числовые функции (они могут быть названы частными критериями оптимизации) образуют векторный критерий
(1)
который
принимает значения в
-мерном
арифметическом пространстве
.
Это
пространство называют критериальным
пространством
или пространством
оценок, а
значение
векторного критерия
при определенном
именуют векторной
оценкой
возможного решения
.
Все векторные оценки образуют в
пространстве
множество
возможных оценок.
Задачу
выбора, содержащую множество возможных
решений
и векторный критерий
,
обычно называют многокритериальной
задачей.
Предположим, что данные компоненты задачи выбора сформированы, четко описаны и зафиксированы. Опыт показывает, что в терминах критерия чаще всего не удается выразить всю гамму «пристрастий», «вкусов» и предпочтений данного ЛПР.
С помощью векторного критерия лишь намечаются определенные цели, которые нередко оказываются весьма противоречивыми.
Эти цели одновременно, как правило, достигнуты быть не могут, и поэтому речь может идти о компромиссном решении.
Задачу векторной оптимизации сформулируем следующим образом: найти
минимум целевых функций
,максимум целевых функций
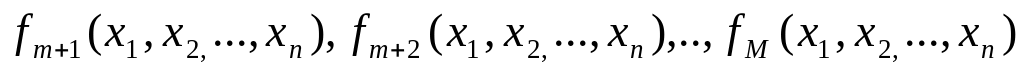
по поисковым переменным при наличии ограничений:
- на поисковые переменные:
, l=1,L; L-число поисковых переменных.
-
на поисковые переменные в виде
функциональных неравенств:
,
j=1,J;
J
- число функциональных неравенств.
- на поисковые переменные в виде функциональных равенств :
, i=1,I. I- число функциональных равенств.
Для сравнения критериев ,имеющих разный физический смысл (и естественно разные размерности),проведем нормализацию критериев в следующем виде:
для целевых функций ,
,
i=1,……..m,
для
целевых функций
i=m+1,…,M.
Эти
функции
сглаживают поверхность значений F и
являются монотонными. Кроме того
,значения
,что
обеспечивает инвариантность к масштабу
изменения критериев.
Это обстоятельство позволяет сформулировать задачу многокритериальной оптимизации в следующем виде:
Найти
минимум целевых функций
по поисковым переменным при наличии ограничений:
- на поисковые переменные:
, l=1,L; L-число поисковых переменных.
- на поисковые переменные в виде функциональных неравенств: , j=1,J; J- число функциональных неравенств.
- на поисковые переменные в виде функциональных равенств :
, i=1,I. I - число функциональных равенств.
(Вильфредо Парето (1848-1923) – итальянский социолог и экономист)