
- •Основные радиотехнические процессы
- •Классификация цепей
- •Классификация сигналов
- •Характеристики детерминированных сигналов
- •Гармонический анализ периодических сигналов
- •Примеры спектров периодических сигналов
- •Распределение мощности в спектре периодического сигнала.
- •Гармонический анализ непериодических сигналов
- •Свойства преобразования Фурье
- •Примеры спектров непериодических сигналов
- •Распределение энергии в спектре непериодического сигнала
- •Соотношение между длительностью сигнала и широтой его спектра
- •Скорость убывания спектра вне основной полосы
- •Модуляция
- •Угловая модуляция.
- •Спектр колебания при угловой модуляции.
- •Спектр колебания при амплитудно-частотной модуляции
- •Узкополосный сигнал
- •Аналитический сигнал
- •Частотные и временные характеристики радиотехнических цепей
- •Апериодический усилитель
- •Резонансный усилитель
- •Обратная связь усилителя
- •Дифференцирующая и интегрирующая цепи
- •Спектральный метод.
- •Операторный метод
- •Метод интеграла наложения.
- •Метод огибающей.
- •Прохождение импульсного сигнала через дифференцирующие и интегрирующие цепи
- •Прохождение радиоимпульса через резонансный усилитель.
- •Прохождение ам – колебаний через резонансный усилитель.
- •Прохождение частотно – модулированного колебания через избирательные цепи.
- •Прохождение фазоманипулированного колебания через резонансную цепь.
Свойства преобразования Фурье
Сдвиг сигнала во времени
Пусть сигнал s1(t) произвольной формы обладает спектральной плотностью S1(W). При задержке этого сигнала на время t0 получим новую функцию времени s2(t)=s1(t-t0). Спектральная плотность сигнала s2(t)
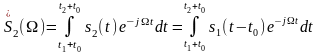 .
.
Введем новую
переменную
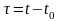 .
Отсюда
.
Отсюда
 .
.
Сдвиг сигнала по оси времени приводит к изменению фазы спектральная плотность, а модуль не зависит от положения сигнала на оси времени.
Изменение масштаба времени
Пусть сигнал s1(t)
подвергается сжатию во времени. Новый
сигнал s2(t)
связан с исходным соотношением
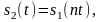 где
где
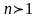 .
.
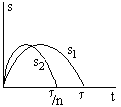
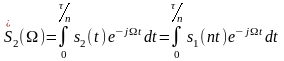 .
.
Введем новую
переменную
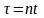 .
Получим
.
Получим
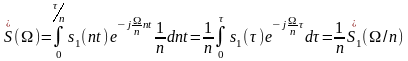 .
.
При сжатии сигнала в n раз во столько же раз расширяется его спектр. Модуль спектральной плотности при этом уменьшается в n раз. При растяжении сигнала во времени имеют место сужение спектра и увеличение модуля спектральной плотности.
Смещение спектра колебаний
Домножим сигнал s(t) на гармонический сигнал cos(w0t+q0). Спектр такого сигнала
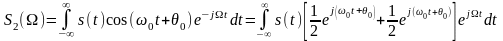
Разобьем его на 2 интеграла
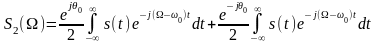 .
.
Полученное соотношение можно записать в следующей форме
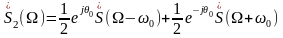
Таким образом, умножение функции s(t) на гармоническое колебание приводит к расщеплению спектра на 2 части, смещенные на ±w0.
Дифференцирование и интегрирование сигнала
Пусть дан сигнал
s1(t)
со спектральной плотностью S1(W).
Дифференцирование этого сигнала 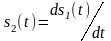 дает соотношение
дает соотношение
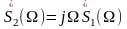 .
.
Интегрирование
сигнала 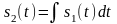 приводит к выражению
приводит к выражению 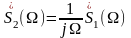
.
Сложение сигналов
При сложении сигналов s1(t) и s2(t) обладающих спектрами S1(W) и S2(W) суммарному сигналу s1(t)+s2(t) соответствует спектр S1(W)+S2(W) (т. к. преобразование Фурье является линейной операцией).
Произведение двух сигналов
Пусть S(t)
представлен произведением двух сигналов:
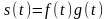 .
Такому сигналу соответствует спектр
.
Такому сигналу соответствует спектр
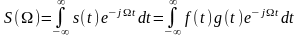
Представим функции в виде интегралов Фурье
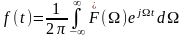 ,
,
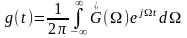 .
.
Где
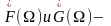 спектральная
плотность сигналов f(t)
b
g(t)
соответственно.
спектральная
плотность сигналов f(t)
b
g(t)
соответственно.
Подставляя второй интеграл в выражение для S(W) получим
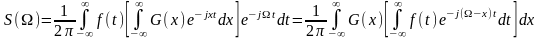
Следовательно
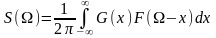 .
.
Т. е. спектр произведения двух функций времени равен свертке их спектров (с коэффициентом 1/2p).
Если
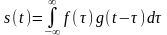 ,
то спектр сигнала будет
,
то спектр сигнала будет
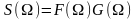 .
.
Взаимная обратимость частоты и времени в преобразовании Фурье
1. Пусть s(t) — четная функция относительно времени.
Тогда
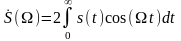 .
То есть функция
.
То есть функция
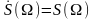 является вещественной и четной
относительно W.
является вещественной и четной
относительно W.
2. Пусть s(t) — нечетная функция относительно времени. При этом:
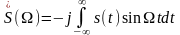 .
.
В этом случае S(W) является нечетной и чисто линейной.
3. Пусть
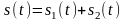 ,
где s1(t)
и s2(t)
– четная и нечетная функции соответственно.
При этом
,
где s1(t)
и s2(t)
– четная и нечетная функции соответственно.
При этом
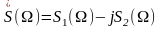 ,
,
4. Предположим, что s(t) — четная функция. Запишем s(t) в виде
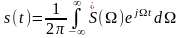 .
Произведем замену W
на t
и t
на W,
учтем, что S(t)
– в данном случае вещественная функция,
получим:
.
Произведем замену W
на t
и t
на W,
учтем, что S(t)
– в данном случае вещественная функция,
получим:
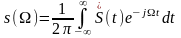 .
.
Таким образом, если сигнал, совпадает по форме с нашим исходным, то его спектр повторяет форму исходного сигнала.
«13» 15-22
