
- •Основные радиотехнические процессы
- •Классификация цепей
- •Классификация сигналов
- •Характеристики детерминированных сигналов
- •Гармонический анализ периодических сигналов
- •Примеры спектров периодических сигналов
- •Распределение мощности в спектре периодического сигнала.
- •Гармонический анализ непериодических сигналов
- •Свойства преобразования Фурье
- •Примеры спектров непериодических сигналов
- •Распределение энергии в спектре непериодического сигнала
- •Соотношение между длительностью сигнала и широтой его спектра
- •Скорость убывания спектра вне основной полосы
- •Модуляция
- •Угловая модуляция.
- •Спектр колебания при угловой модуляции.
- •Спектр колебания при амплитудно-частотной модуляции
- •Узкополосный сигнал
- •Аналитический сигнал
- •Частотные и временные характеристики радиотехнических цепей
- •Апериодический усилитель
- •Резонансный усилитель
- •Обратная связь усилителя
- •Дифференцирующая и интегрирующая цепи
- •Спектральный метод.
- •Операторный метод
- •Метод интеграла наложения.
- •Метод огибающей.
- •Прохождение импульсного сигнала через дифференцирующие и интегрирующие цепи
- •Прохождение радиоимпульса через резонансный усилитель.
- •Прохождение ам – колебаний через резонансный усилитель.
- •Прохождение частотно – модулированного колебания через избирательные цепи.
- •Прохождение фазоманипулированного колебания через резонансную цепь.
Примеры спектров периодических сигналов
1. Последовательность прямоугольных импульсов.

Здесь .
 ,
где
,
где
 -скважность
-скважность
,
так как функция s(t)
– четная,
 .
.

 .
.
Спектр имеет вид:

При
 ,
то есть
,
то есть
 (радиолокационный сигнал) и
(радиолокационный сигнал) и

 .
.

2. Прямоугольное
колебание.
Подобное колебание, часто называемое
меандром
(Меандр — греческое слово, обозначающее
“орнамент”), находит особенно широкое
применение в измерительной технике.
Здесь
 ,
,
 .
.

Спектр меандра
3. Последовательность пилообразных импульсов.

 .
.
Функция s(t) – нечетная, поэтому разложение в ряд Фурье содержит только синусоидальные составляющие.
4. Последовательность треугольных импульсов.

 .
.
Данная функция содержит только косинусоидальные члены в силу четности функции. Амплитуды гармоник с ростом n убывают быстрее, чем в предыдущих случаях, так как высокочастотные составляющие для образования сигнала не нужны.

Спектр последовательности треугольных импульсов
При
 сумма ряда
сумма ряда
 приближается к
приближается к
 всюду, кроме точек разрыва функции, где
образуются выбросы.
всюду, кроме точек разрыва функции, где
образуются выбросы.
При величина этого выброса равна 1,18E. Этот дефект сходимости (18%) носит название явления Гиббса. Но ряд сходится в среднем, то есть выбросы бесконечно узкие и не вносят ощутимого вклада в усреднение.


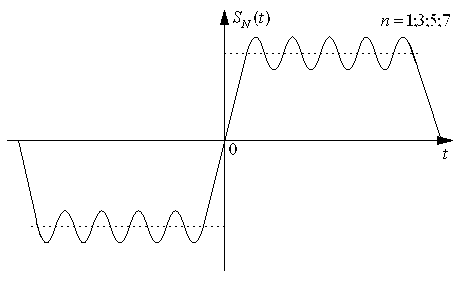 .
.
10
Распределение мощности в спектре периодического сигнала.
 .
.
 .
.
Если
 – ток, то мощность, выделяемая на
сопротивлении R.
– ток, то мощность, выделяемая на
сопротивлении R.
 .
.
 .
Средняя мощность не зависит от фаз
отдельных гармоник.
.
Средняя мощность не зависит от фаз
отдельных гармоник.
11
Гармонический анализ непериодических сигналов
Пусть сигнал s(t) задан в виде некоторой функции, отличной от нуля в промежутке (t1,t2). Этот сигнал должен быть интегрируем на интервале (t1,t2).
Возьмем бесконечный
отрезок времени Т, включающий в себя
промежуток (t1,t2).
Тогда сигнал S(t)
является, как бы периодическим с периодом
T→
∞, а
 .
.
Заданный сигнал можно представить в виде ряда Фурье, где

На основании этого получим:

Поскольку Т®µ, то сумму можно заменить интегралом, а W1 на dW и nW1 на W. Таким образом, мы прейдем к двойному интегралу Фурье:
 ,
,
Где
 — спектральная плотность сигнала. Когда
интервал (t1,t2)
не уточнен, интеграл имеет бесконечные
пределы.
— спектральная плотность сигнала. Когда
интервал (t1,t2)
не уточнен, интеграл имеет бесконечные
пределы.
Это есть обратное и прямое преобразование Фурье, соответственно.
Спектр непериодического
сигнала является сплошным

Если сравнить выражения для огибающей сплошного спектра (модуль спектральной плотности) непериодического сигнала и огибающей линейчатого спектра периодического сигнала, совпадающего на интервале (t1,t2) с непериодическим сигналом, то будет видно, что они совпадают по форме.
Учитывая, что
 ,
получим:
,
получим:
 ,
,
но отличаются
масштабами
 .
.
Следовательно,
спектральная плотность
 обладает всеми основными свойствами
комплексного ряда Фурье. Т. е. можно
записать
обладает всеми основными свойствами
комплексного ряда Фурье. Т. е. можно
записать
 ,
,
где
 ,
,
 ,
,
спектральная
плотность:

Модуль спектральной
плотности является четной функцией и его можно
рассматривать как амплитудно-частотную
характеристику сигнала. Аргумент
является четной функцией и его можно
рассматривать как амплитудно-частотную
характеристику сигнала. Аргумент — нечетная функция, рассматриваемая
как фазо-частотная характеристика
сигнала.
— нечетная функция, рассматриваемая
как фазо-частотная характеристика
сигнала.
На основании этого сигнал можно выразить следующим образом

Из четности модуля и нечетности фазы следует, что подынтегральная функция в первом случая является четной, а во втором — нечетной относительно W. Следовательно, второй интеграл равен нулю (нечетная функция в симметричных пределах) и окончательно
 .
.
Отметим, что при W=0 выражение для спектральной плотности равно площади под кривой s(t)
 ,
,
то есть
 имеет значение, равное площади сигнала.
имеет значение, равное площади сигнала.
12
