Прохождение ам – колебаний через резонансный усилитель.

На вход одноконтурного усилителя, воздействует колебание

.

Требуется выявить структуру колебания на выходе усилителя.

Колебательный контур, входящий в состав усилителя, является инер­ционной цепью, что не может не оказать влияния на параметры выходного колебания.

В данном случае простейшей гармонической модуляции амплитуды, когда спектр колебания содержит всего лишь три составляющих, структуру коле­бания на выходе усилителя проще всего отыскать, рассматривая прохож­дение через усилитель каждой из составляющих отдельно.

Записав выражение в форме

.

найдем передаточные функции усилителя для частот , , и .

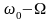Положим (точная настройка колебательного контура на несущую частоту ), получаем:

для несущей частоты

для боковой частоты

для боковой частоты

где — фазовый сдвиг в колебательном контуре на боковых частотах (запаздывание на верхней и опережение на нижней боковых часто­тах).

С учетом амплитудных и фазовых изменений, претерпеваемых спектраль­ными составляющими в усилителе, можно представить выходное колебание в форме:

Свернув это выражение, получим:

.

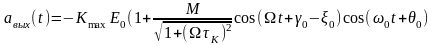Как и следовало ожидать, частота и фаза АМ колебания при прохождении через резонансный усилитель не изменяются.

Инерционность колебательной цепи влияет на огибающую колебания:

1) глубина модуляции на выходе

меньше, чем на входе; относительное уменьшение глубины модуляции, иногда называемое коэффициентом демодуляции:

.

2) огибающая амплитуд- н.э. выходе отстает по фазе от огибающей вход­ного колебания на угол

.

Оба эти фактора обусловлены тем, что инерционность колебательной цепи снижает скорость изменения во времени огибающей колебания. При этом, однако, форма огибающей остается неизменной (гармонической).

Смысл этого результата поясняется рис. 6.19, а, на котором показано положение спектра входного колебания относительно резонансной харак­теристики колебательного контура. Чем выше частота модуляции Ω, тем больше относительное ослабление амплитуды колебаний боковых частот и, следовательно, меньше глубина модуляции колебания.

Рис. Положение спектра модулированного колебания относительно частотной ха­рактеристики усилителя: a) при точной настройке; б) при расстройке.

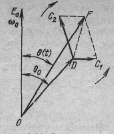
Рис. Возникнове­ние паразитной фазо­вой модуляции при асимметрии амплитуд колебаний боковых частот.

Полученные из анализа тональной модуляции результаты позволяют представить общую картину явлений при передаче через контур колебаний, модулированных по амплитуде сложным сообщением. Входящим в такое сообщение различным частотам Ω, соответствует неоди­наковое ослабление: чем выше частота, тем сильнее выражена демодуляция. Так как при приеме колеба­ний напряжение на выходе детектора приемника пропорционально коэффициенту модуляции, полу­чается относительное ослабление высших частот сооб­щения. Таким образом, зависимость 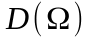определяет степень линейных частотных искажений передаваемого сообщения. Подобные искажения называются линейными потому, что они не сопровождаются возникновением новых частот. Имеет место также и задержка сообщения. Это объясняется тем, что фазовый сдвиг огибающей (при тональной модуляции) зависит от частоты. Колеба­тельный контур влияет на сообщение, содержащееся в огибающей, так же, как и фильтр нижних частот при пропускании непосредственно через него сообщения.

Задержка определяется наклоном ФЧХ

.

Обычно задержку определяют по наклону ФЧХ в точке Ω = 0.

Итак, задержка сообщения в одиночном контуре, полоса прозрачности которого достаточна для удовлетворительного пропускания спектра со­общения, равна постоянной времени контура.

Рассмотрим теперь случай неточной настройки контура на несущую ча­стоту модулированного колебания. Несовпадение частот и приводит к асимметрии боковых частот на выходе усилителя. Возник­новение асимметрии поясняется векторной диаграммой выходных напря­жений, представленной на рис На этой диаграмме вектор ОВ изобра­жает несущее колебание, фаза которого запаздывает относительно фазы вход­ной ЭДС (принятой равной нулю) на угол 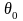(так как рис. соответ­ствует положительной расстройке . Амплитуда коле­бания верхней боковой частоты (вектор ВС) в данном случае значительно меньше амплитуды колебания нижней боковой частоты (вектор DC2). Длина равнодействующего вектора OF, изображающего результирующее колебание, изменяется по сложному закону, не совпадающему с гармоническим законом изменения огибающей входной ЭДС.

Следует иметь в виду, что для восстановления передаваемого сообщения на выходе радиолинии, работающей с амплитудной модуляцией, применя­ется амплитудный детектор, представляющий собой нелинейное устройство. Напряжение на выходе детектора пропорционально огибающей модулиро­ванного колебания. Из этого следует, что нарушение симметрии амплитуд и фаз колебаний боковых частот при неточной настройке контура на несущую частоту приводит к нелинейным искажениям передаваемых сообщений. Эти искажения проявляются в возникновении новых частот, кратных частоте Ω полезной модуляции.

Кроме искажения формы огибающей амплитуд, возникает также пара­зитная фазовая модуляция колебания, так как при вращении векторов DC1 и DC2 (см. рис. 6.20) непрерывно изменяется фаза вектора OF относительно фазы несущего колебания (принятой в качестве исходной). В неко­торых случаях это может привести к дополнительным искажениям сигнала. Полученные выше результаты нетрудно распространить на любую коле­бательную цепь, например на связанные контуры. Если резонансная кри­вая такой цепи симметрична относительно несущей частоты , то правую ветвь этой кривой можно рассматривать как характеристику коэффициента D.

??