
- •Основные радиотехнические процессы
- •Классификация цепей
- •Классификация сигналов
- •Характеристики детерминированных сигналов
- •Гармонический анализ периодических сигналов
- •Примеры спектров периодических сигналов
- •Распределение мощности в спектре периодического сигнала.
- •Гармонический анализ непериодических сигналов
- •Свойства преобразования Фурье
- •Примеры спектров непериодических сигналов
- •Распределение энергии в спектре непериодического сигнала
- •Соотношение между длительностью сигнала и широтой его спектра
- •Скорость убывания спектра вне основной полосы
- •Модуляция
- •Угловая модуляция.
- •Спектр колебания при угловой модуляции.
- •Спектр колебания при амплитудно-частотной модуляции
- •Узкополосный сигнал
- •Аналитический сигнал
- •Частотные и временные характеристики радиотехнических цепей
- •Апериодический усилитель
- •Резонансный усилитель
- •Обратная связь усилителя
- •Дифференцирующая и интегрирующая цепи
- •Спектральный метод.
- •Операторный метод
- •Метод интеграла наложения.
- •Метод огибающей.
- •Прохождение импульсного сигнала через дифференцирующие и интегрирующие цепи
- •Прохождение радиоимпульса через резонансный усилитель.
- •Прохождение ам – колебаний через резонансный усилитель.
- •Прохождение частотно – модулированного колебания через избирательные цепи.
- •Прохождение фазоманипулированного колебания через резонансную цепь.
Дифференцирующая и интегрирующая цепи
В радиоэлектронике часто необходимо осуществить дифференцирование или интегрирование сигнала. Дифференцирование и интегрирование являются линейными математическими операциями. Следовательно, следует применять линейные цепи и элементы. Этим требованиям отвечают конденсаторы и катушки индуктивности в сочетании с резистором при надлежащем съеме выходного сигнала.
Дифференцирующая цепь
Уравнение для тока в цепи: . После дифференцирования: .
Если обозначить , то . Обозначим CR через t –– постоянная времени цепи.
Проанализируем. Если очень большое, то это быстрый процесс ( ). При этом, в случае отсутствия постоянной составляющей в сигнале,
Если мала, то это медленный процесс ( ). При этом
Следовательно: дифференцирующая цепь дифференцирует медленные процессы и пропускает без изменения быстрые процессы.
Передаточная функция цепи:
если t мала, то
если t большая, то
Переходная характеристика:
Интегрирующая цепь
В этом случае .
Если RC большое (быстрый процесс), то .
Если КС мало (медленный процесс), то .
Следовательно интегрирующая цепь интегрирует быстрые процессы и пропускает без изменения медленные.
Передаточная функция:
Переходная характеристика:
??
Спектральный метод.
В основе этого
метода лежит использование передаточной
функции цепи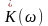 .
Если на входе линейного четырехполюсника
действует сигнал произвольной формы в
виде ЭДС е (t), то, применяя спектральный
метод, следует определить спектральную
плотность входного сигнала
.
Если на входе линейного четырехполюсника
действует сигнал произвольной формы в
виде ЭДС е (t), то, применяя спектральный
метод, следует определить спектральную
плотность входного сигнала
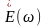 .
Умножением
на
определяется
спектральная плотность сигнала на
выходе четырехполюсника. Наконец,
применение к произведению
обратного преобразования Фурье определяет
выходной сигнал в виде функции времени.
.
Умножением
на
определяется
спектральная плотность сигнала на
выходе четырехполюсника. Наконец,
применение к произведению
обратного преобразования Фурье определяет
выходной сигнал в виде функции времени.
Таким образом,
если входной сигнал записан в виде
интеграла:

то выходной
сигнал можно представить в аналогичной
форме
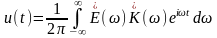 .
.
Сигнал на выходе линейной цепи можно получить суммированием составляющих спектра входного сигнала, взятых с весом . Иными словами, передаточная функция цепи является весовой функцией, определяющей относительный вклад различных составляющих спектра в сигнал u (t).
Операторный метод
Анализ переходных
процессов значительно упрощается
при представлении как внешнего
воздействия, так и передаточной функции
в виде преобразований Лапласа. При этом
обозначение передаточной функции
можно сохранить прежним, а изменить
только аргумент, так что
перейдет в
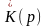 .
Функция же
переходит в
.
Функция же
переходит в
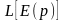 .
Преобразование Лапласа от функции
времени е (t) в дальнейшем обозначается
символом
.
Преобразование Лапласа от функции
времени е (t) в дальнейшем обозначается
символом
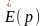 .
При этом получаем:
.
При этом получаем:
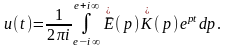
При t > 0 замкнутый контур интегрирования, образованный добавлением дуги бесконечно большого радиуса в левой полуплоскости, охватывает все полюсы подынтегральных функций как , так и , благодаря чему имеет место соотношение:
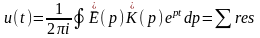 при t>0,
при t>0,
(здесь
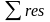 — сумма вычетов в указанных полюсах).
— сумма вычетов в указанных полюсах).
При t < 0 контур интегрирования лежит в правой полуплоскости, не содержит полюсов и интеграл равен нулю.
Показанное на
рисунке расположение полюсов функции
(на мнимой оси) соответствует ЭДС
вида
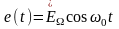 ,
существующей при
,
существующей при
Итак, вычисление
интеграла сводится к определению вычетов
в полюсах подынтегральной функции.
Представим подынтегральную функцию
выражения в виде:
В данном случае
знаменатель D(p) образуется произведением
множителей вида (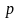 —
—
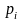 ),
где
— полюсы не только функции
,
но и функции
),
где
— полюсы не только функции
,
но и функции

Тогда вычет функции С(p)/D(p), имеющей в точке рi простой полюс (первой кратности), определится формулой

Если функция C(p)/D(p) имеет в точке рi полюс кратности k (k — целое положительное число), то
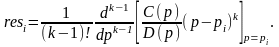
Методика применения контурных интегралов для определения некоторых функций, играющих большую роль в теории переходных процессов, будет в дальнейшем пояснена на примерах.
??
