Szereg rozdzielczy

Obszar zmienności wartości cech dzielimy na rozłączne przedziały w postaci

dla i=1,2,...,k. Są to przedziały prawostronnie otwarte. Jednostki statystyczne , których wartości cechy przedstawia szereg szczegółowy prosty grupujemy wykorzystując przedziały, które nazywać będziemy przedziałami klasowymi lub klasami. Wyniki grupowania zawiera poniższa tablica

Tab.2 Wyniki grupowania statystycznego

Przedział klasowy	Liczebność	środek przedziału klasowego	Częstość względna
. . .	. . .	. . .	. . .
Razem

Źródło: Opracowanie własne

Wartość środkową oblicza się według następującej formuły :

( i=1,2,...,k)

Przy budowie szeregu rozdzielczego należy sobie odpowiedzieć na następujące pytania :

1. czy długości przedziałów mają być jednakowe ?

2. na ile klas należy podzielić obszar zmienności ?

W praktyce badań statystycznych wygodnie jest, gdy przedziały klasowe są jednakowej długości. W przypadku , gdy przedziały nie są jednakowej długości, do opisu struktury zbiorowości wykorzystać należy tzw. gęstość liczebności, definiowaną za pomocą następującego wzoru :

( i=1,2,...,n )

gdzie w mianowniku mamy długość i-tego przedziału, w liczniku zaś odpowiadającą mu liczebność.

W badaniach statystycznych brak jest jednoznacznych kryteriów umożliwiających w sposób jednoznaczny odpowiedzieć na pytanie o liczbę klas w szeregu rozdzielczym.

J. Spława Neyman zalecał przy tworzeniu szeregów rozdzielczych podział obszaru zmienności na około 10 – 20 klas, w zależności od liczebności zbiorowości.

Oznaczmy symbolem „ h „ długość przedziału klasowego. Załóżmy, że wszystkie przedziały mają mieć równą długość. W tym przypadku najczęściej zaleca się, aby długość przedziału obliczać za pomocą następującej formuły :

( i=1,...,n)

gdzie : w liczniku jest zakres zmienności wartości cechy, w mianowniku zaś liczba wymaganych klas.

Jeśli decydujemy się na budowę przedziałów klasowych , to narażamy się na pewną stratę informacji dotyczących pojedynczych wyników. Im większa jest rozpiętość przedziału klasowego, tym ta strata może być bardziej dotkliwa.

Przedziały klasowe zapisuje się zazwyczaj z dokładnością do przyjętej jednostki pomiarowej. Można budować rozkłady ( szeregi ) z przedziałami klasowymi domkniętymi lub otwartymi.

Rozstęp wynosi R= X_max – X_min . Rozstęp charakteryzuje jedynie wstępnie dyspersję badanego rozkładu.

Odchylenie ćwiartkowe wyrażone jest następującym wzorem :

Najpierw należy obliczyć kwartyl trzeci i kwartyl pierwszy.

Grupy dochodów miesięcznych na gospodarstwo domowe	Liczba kobiet W %	Szereg skumulowany
0,5 – 1,0	0,9	0,9
1,0 – 1,5	4,0	4,9
1,5 – 2,0	8,8	13,7
2,0 – 3,0	21,5	35,2 Q1
3,0 – 4,0	23,5	58,7 Q2
4,0 – 5,0	20,3	79,0 Q3
5,0 – 6,0	10,8	89,8
6,0 – 7,0	5,2	95,0
7,0 – 8,0	2,8	97,8
8,0 – 9,0	2,2	100,0

Wzory:

Odchylenie ćwiartkowe wynosi :

Oznacza to , że średnio miesięczne dochody kobiet różnią się od mediany o tyś. zł.

Mediana dla badanego rozkładu wynosi :

Współczynnik zmienności ( względna miara dyspersji )wynosi:

Oznacza to , że 31,32 % mediany dochodów kobiet stanowi odchylenie standardowe.

Wyznaczenie dominanty według wzoru :

Podstawowym miernikiem asymetrii jest różnica między średnią arytmetyczną a dominantą, czyli :

Znak „ – „ przy wartości miernika oznacza asymetrię lewostronną , znak „+” asymetrię prawostronną.

W rozpatrywanym przykładzie mamy do czynienia z asymetrią prawostronną , co oznacza , że przewaga liczebności występuje w przedziałach klasowych poniżej średniej arytmetycznej.

O sile i kierunku symetrii mówią współczynniki asymetrii. Współczynnik asymetrii Pearsona wyznacza się według formuły :

Współczynnik asymetrii wykazuje skośność prawostronną.

Gdy rozkład jest symetryczny to , V_s = 0

Gdy rozkład jest asymetryczny – prawostronny., to V_s > 0

Gdy rozkład jest asymetryczny – lewostronny , to V_s < 0

Współczynników asymetrii jest kilka, a zastosowanie ich jest uzależnione od charakteru badanego szeregu i możliwości wyliczenia poszczególnych parametrów.

Miarą asymetrii jest również współczynnik skośności obliczony na podstawie dominanty i mediany, według wzoru :

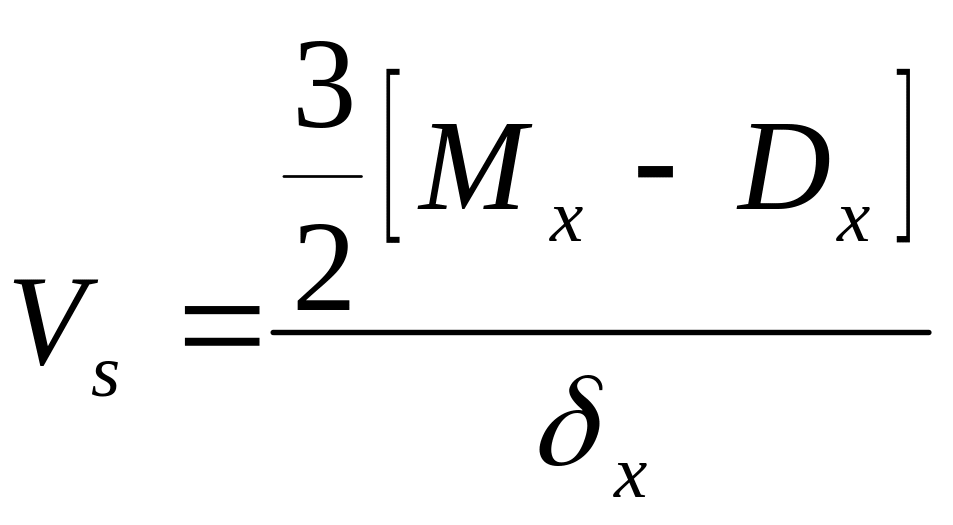
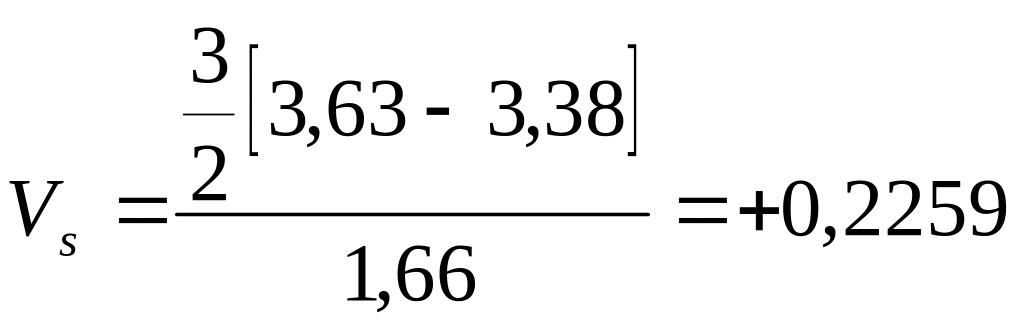
Miarą asymetrii może być także moment trzeci centralny. Dla rozkładu przedziałowego ma on postać następującą:

Tablica pomocnicza do wyznaczenia momentu trzeciego centralnego

0,75	0,9	-3,063	-25,863
1,25	4,0	-2,563	-67,344
1,75	8,8	-2,063	-77,263
2,50	21,5	-1,313	-48,665
3,50	23,5	-0.313	-0,720
4,50	20,3	0,687	6,581
5,50	10,8	1,687	51,851
6,50	5,2	2,687	100,879
7,50	2,8	3,687	140,336
8,50	2,2	4,687	226,519
Razem	100		306,313

Dla badanego szeregu moment trzeci centralny wynosi :

Moment trzeci centralny można również zapisać w postaci momentów zwykłych w sposób następujący:

gdzie :

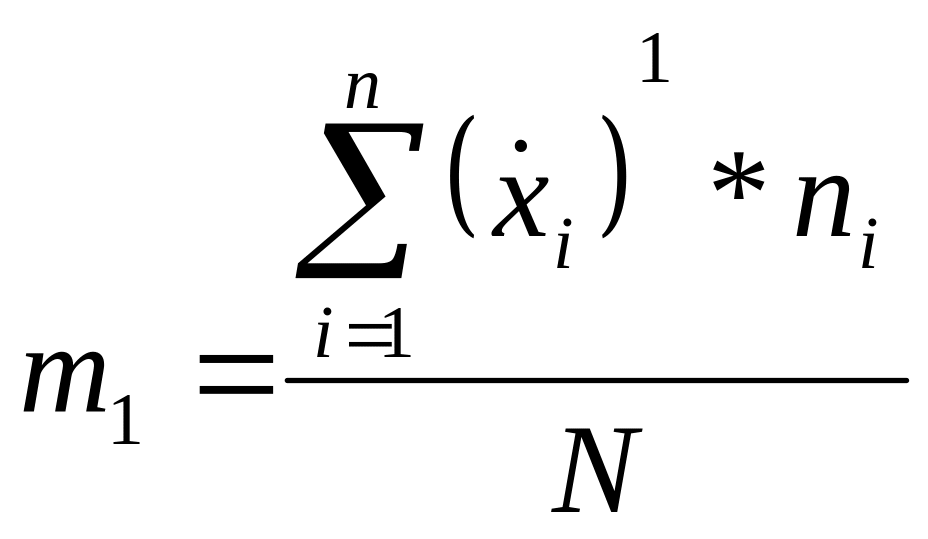
Dla szeregu wynoszą odpowiednio :

wobec tego otrzymujemy :

Miarą względną asymetrii jest następująca formuła :

Dla rozpatrywanego szeregu wynosi :

Rozkład ma asymetrię prawostronną o natężeniu 0,66.

Dla szeregów dokładnie symetrycznych m₃=0. W przypadku asymetrii prawostronnej m₃ > 0, lewostronnej zaś m₃ < 0.

Przykład 3.

Zbiór województw , w którym cechą badania była ich powierzchnia, został opisany przy użyciu podstawowych charakterystyk liczbowych tj średniej arytmetycznej, która wynosi 6,286 tyś. km² oraz odchylenia standardowego ,które jest równe 2, 138 tyś, km².W celu dokładniejszego opisu rozkładu tej zbiorowości należy wyznaczyć miary koncentracji.

Powierzchnia W tyś. km2	Liczba Wojewódz.
1-3	1	2	-4,286	337,449405
3-5	14	4	-2,286	382,325213
5-7	18	6	-0,286	0,12043
7-9	10	8	1,714	86,306453
9-11	5	10	3,714	951,344040
11-13	1	12	5,714	1066,009178
	49			2823,554720

Względna miara koncentracji to stosunek momentu centralnego czwartego rzędu przez odchylenie standardowe do potęgi czwartej, czyli :

Im wyższa wartość K , tym bardziej wysmukła jest krzywa liczebności , co wskazuje na tendencję do skupienia się jednostek wokół średniej. Małe wartości wskazują na spłaszczenie krzywej rozkładu , a zatem słabą koncentrację. Zakłada się ,że dla rozkładu normalnego K=3, dla bardziej od niego spłaszczonego K < 3 oraz dla wysmukłego K > 3. W związku z powyższym skonstruowany współczynnik koncentracji o postaci :

przyjmuje wartość zero, jeżeli rozkład ma kształt normalny ,K_u > 0 , jeżeli rozkład jest bardziej wysmukły, oraz K_u < 0 , gdy rozkład jest spłaszczony w stosunku do rozkładu normalnego.

Koncentracja w porównaniu z krzywą normalną jest słabsza, a zatem rozkład jest spłaszczony.

Inną miarą koncentracji jest współczynnik koncentracji Lorenca. Zjawisko koncentracji może być rozważane jako nierównomierny podział ogólnej sumy wartości zmiennej x pomiędzy poszczególne jednostki zbiorowości statystycznej. Ma to miejsce przy badaniu dochodów, koncentracji produkcji, gęstości zaludnienia, rozmieszczenia bogactw naturalnych itp. Tak rozumiana koncentracja jest zwykle przedstawiana i mierzona za pomocą krzywej koncentracji Lorenza. Kształt krzywej określa natężenie koncentracji. Współczynnik koncentracji Lorenza ( K_L ) można wyrazić za pomocą wzoru:

gdzie :

a – pole zawarte między linią równomiernego podziału a krzywą Lorenza

b – pole pod krzywą Lorenza

a+b – pole trójkąta

Wyznaczenie pola a nie jest łatwe. Częściej wyznaczamy przybliżoną wartość pola b, budując w tym celu w układzie współrzędnych prostokąty o podstawie równej wskaźnikowi struktury dla liczby jednostek znajdujących się w przedziale, a wysokość jest średnią ze skumulowanych wartości wskaźników struktury wielkości badanego zjawiska grupy badanej i poprzedniej. Obliczenie powierzchni pola b można opisać następującym wzorem:

gdzie :

skum.W_i – kolejne skumulowane wartości wskaźników struktury wielkości badanego zjawiska

- kolejne wartośći wskaźników struktury dla liczby badanych jednostek

Współczynnik ten jest względną miarą koncentracji zjawiska. W praktyce zawiera się

Przykład 4.

Struktura zatrudnienia w badanych firmach została scharakteryzowana za pomocą następujących liczb zawartych w poniższej tablicy. Należy określić stopień koncentracji zatrudnienia w badanych firmach w 1995 roku .

Liczba zatrudnionych pracowników w badanych firmach	Firmy w %	Zatrudnienie w %
do 4	37,7	1,0
5 - 10	20,5	2,0
11-15	7,2	1,3
16 - 50	17,4	7,0
51 -100	7,0	6,8
101 - 200	4,3	8,2
201 - 500	3,1	13,2
501 -1000	1,5	14,3
1001 - 2000	0,7	13,7
2001 - 5000	0,4	17,7
5001 i więcej	0,2	14,8
	100	100

Źródło: Dane umowne

Tablica pomocnicza do wyznaczenia do wyznaczenia współczynnika Lorenza

Firmy w %	Zatrudnienie w %	Skum.	Skum.
37,7	1,0	37,7	1,0	(1+0)/2=0,5	0.5*37,7=18,85
20,5	2,0	58,2	3,0	( 3,0+1,0)/2=2,0	2,0*20,5=41,00
7,2	1,3	65,4	4,3	( 4,3+3,0)/2=3,65	3,65*7,2=26,28
17,4	7,0	82,8	11,3	( 11,3 + 4,3 ) /2=7,80	7,80*17,4=135,72
7,0	6,8	89,8	18,1	14,7	102,90
4,3	8,2	94,1	26,3	22,20	95,46
3,1	13,2	97,2	39,5	32,90	101,99
1,5	14,3	98,7	53,8	46,65	69,975
0,7	13,7	99,4	67,5	60,65	42,455
0,4	17,7	99,8	85,2	76,35	30,54
0,2	14,8	100,0	100,0	92,80	18,52
100	100				683,69

Źródło: Obliczenia własne

Obliczona powierzchnia b wynosi 683,69, wobec tego współczynnik koncentracji wynosi:

Pole trójkąta ( a + b)=5000, wobec tego

Oznacza to dość wysoką koncentrację badanego zjawiska.

Inną miarą koncentracji jest współczynnik koncentracji Lorenza. Może być on wykorzystywany do badań w zakresie koncentracji własności ziemskiej, bogactw naturalnych czy kapitału. Punktem wyjścia do ilościowego badania koncentracji jest ustalenie, w jaki sposób rozkłada się ogólna suma wartości badanej cechy na poszczególne jednostki zbiorowości statystycznej.

Do oceny stopnia natężenia tak rozumianej koncentracji stosuje się krzywą koncentracji lub krzywą Lorenza. Kształt linii łamanej określa natężenie koncentracji Jeżeli na każdą jednostkę zbiorowości przypada taka sama część ogólnej sumy wartości cechy , to zamiast krzywej koncentracji otrzymamy linię prostą przechodzącą przez początek układu współrzędnych pod kątem =45 w stosunku do osi odciętych. Jest to tzw. Linia równomiernego rozkładu wartości cechy dla poszczególnych jednostek zbiorowości.

Stosunek pola zawartego między krzywą koncentracji a linią równomiernego rozkładu do ogólnego pola trójkąta nosi nazwę współczynnika koncentracji Lorenza.Można go wyznaczyć w sposób następujący:

gdzie :

a – powierzchnia pola zawartego między krzywą koncentracji a linią równomiernego rozkładu

b – powierzchnia pola leżącego pod krzywą koncentracji

Współczynnik ten zawiera się w przedziale [ 0, 1 ]. Procedurę wyznaczania współczynnika przedstawimy na przykładzi

Przykład 4.Na podstawie danych dotyczących osób pobierających renty z tytułu niezdolności do pracy według wysokości świadczeń we wrześniu 1997 roku należy ocenić stopień koncentracji wysokości świadczeń z ubezpieczenia społecznego.

Obliczenia pomocnicze do wyznaczenia współczynnika koncentracji.

Wysokość Świadczenia Brutto Z ubezp.społ.	Liczba Pobier. Renty Z tytuł.niezd. Do pracy ni	Łączna Wysok. Świadcz. Brutto	Odsetki Liczby Pobier. Renty	Odsetki Łączn. Wysok. Świadcz.	Skum.	Skum.	Pole figury b
400-450	255,6	108 630,0	0,159	0,101	0,159	0,101	0.0080
450-500	387,5	184 062,5	0,241	0,172	0,400	0,273	0.0451
500-550	191,0	100 275,0	0,119	0,093	0,518	0,366	0.0379
550 -600	142,6	81 955,0	0,089	0,076	0,607	0,443	0,0359
600-650	104,9	65 562,5	0,065	0,061	0,672	0,504	0,0309
650-700	88,8	59 940,0	0,055	0,056	0,727	0,560	0,0294
700-750	61,9	44 877,5	0,038	0,042	0,766	0,602	0,0223
750-800	48,4	37 510,0	0.030	0,035	0,796	0,636	0,0186
800-900	72,6	62 710,0	0,0,45	0,058	0,841	0,694	0,0300
900-1 000	48,4	45 980,0	0,030	0,043	0,871	0,737	0,0215
1 000 – 1 100	40,3	42 315,0	0,025	0,039	0,896	0,776	0,0190
1 100 - 1 200	29,6	34 040,0	0,018	0,032	0,915	0,808	0,0146
1 200 – 1 300	29,6	37 000,0	0,018	0,034	0,933	0,843	0,0152
1 300 – 1 400	29,6	39 960,0	0,018	0,037	0,952	0,880	0,0158
1 400 – 1 500	16,1	23 345,0	0,010	0,022	0,962	0,902	0,0089
1 500 – 1 600	10,7	16 585,0	0,007	0,015	0,968	0,917	0,0060
1 600 – 1 700	5,6	9 240,0	0,003	0,009	0,972	0,926	0,0032
1 700 – 1 800	45,6	79 800,0	0,028	0,074	1,000	1,000	0,0273
Ogółem	1 608,8	1 072 828,5	1,000	1,000			0,3896

Zaliaś A. : Metody statystyczne. PWE, Warszawa, s.75.

Pole figury b pod krzywą Lorenza , można w przybliżeniu wyznaczyć w sposób następujący:

gdzie :

cum z_i – względna wartość szeregu skumulowanego obliczonego w sposób następujący

w_i - liczebności względne obliczone następująco: , przy czym

W naszym przykładzie mamy :

a=0,5-0,3896=0,1104

Uzyskany wynik wskazuje na słaby stopień koncentracji, co odpowiada równomiernemu podziałowi łącznej wysokości świadczenia brutto z ubezpieczenia społecznego między pobierających renty z tytułu niezdolności do pracy.