Test dla wskaźnika struktury

Niech populacja generalna ma rozkład dwupunktowy z parametrem p oznaczającym prawdopodobieństwo , że badana zmienna X w populacji przyjmie wyróżnioną wartość. Parametr p ( )<p<1 ) można interpretować jako frakcję elementów populacji mających tę wartość określaną często w literaturze wskaźnikiem struktury w populacji.

Załóżmy dalej , że dla takiej populacji chcemy zweryfikować hipotezę zerową , że parametr p w populacji ma określoną wartość . Hipoteza zerowa jest postaci Sprawdzianem tej hipotezy jest wskaźnik struktury z dużej próby n –elementowej

zdefiniowany jako :

( 1 )

gdzie m oznacza liczbę wyróżnionych elementów w próbie i jest realizacją zmiennej losowej X o rozkładzie dwupunktowym.

Statystyka ( 1 ) ma asymptotyczny ( graniczny ) rozkład normalny . Jeżeli hipoteza zerowa jest prawdziwa , tzn. jeśli , to wskaźnik struktury z próby ma asymptotyczny rozkład normalny 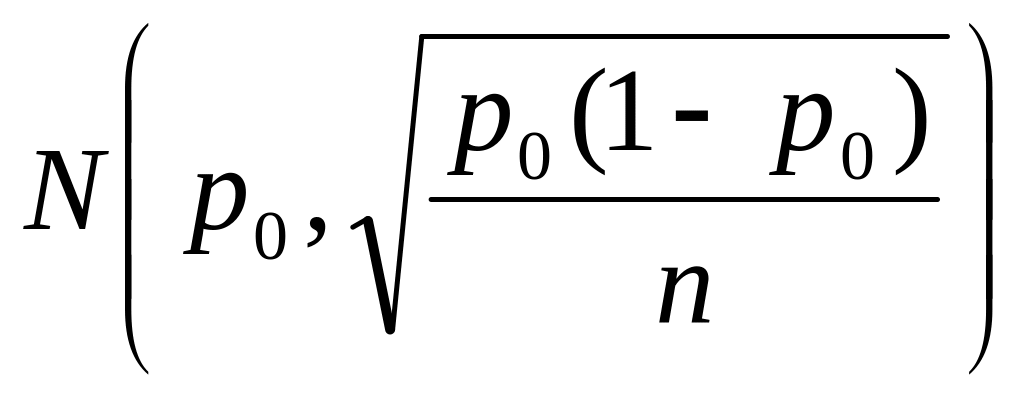i statystyka :

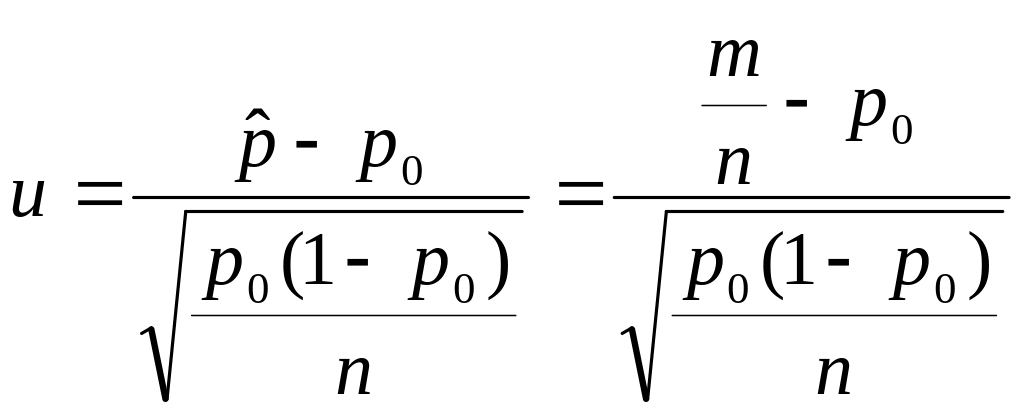
ma asymptotyczny ( w przybliżeniu ) rozkład normalny N( 0,1 ), przy czym m oznacza liczbę jednostek o wyróżnionej wartości cechy w n – elementowej próbie . Obszar krytyczny w tym teście jest określony relacją , gdzie jest poziomem istotności , a - wartością krytyczną.

Sposób weryfikacji przebiega w podobny sposób jak poprzednio. Można konstruować również jednostronne obszary krytyczne w zależności od sformułowania hipotezy alternatywnej.

Test dla dwóch wskaźników struktury

Niech badana cecha X w dwóch populacjach ma rozkład dwupunktowy z parametrami i . Formułujemy hipotezę , że oba te parametry są identyczne . Hipotezę zerową możemy zapisać w sposób następujący : a hipotezę alternatywną albo lub . W celu weryfikacji hipotezy zerowej z obu populacji wylosowano próby proste o liczebności jednostek. Niech oraz oznaczają wskaźniki struktury odpowiednio z pierwszej i drugiej próby . Różnica tych wskaźników struktury ma asymptotyczny rozkład :

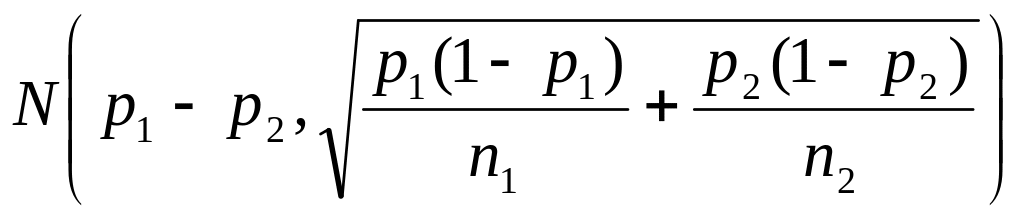
Jeśli prawdziwa jest hipoteza zerowa ( ), to statystyka :

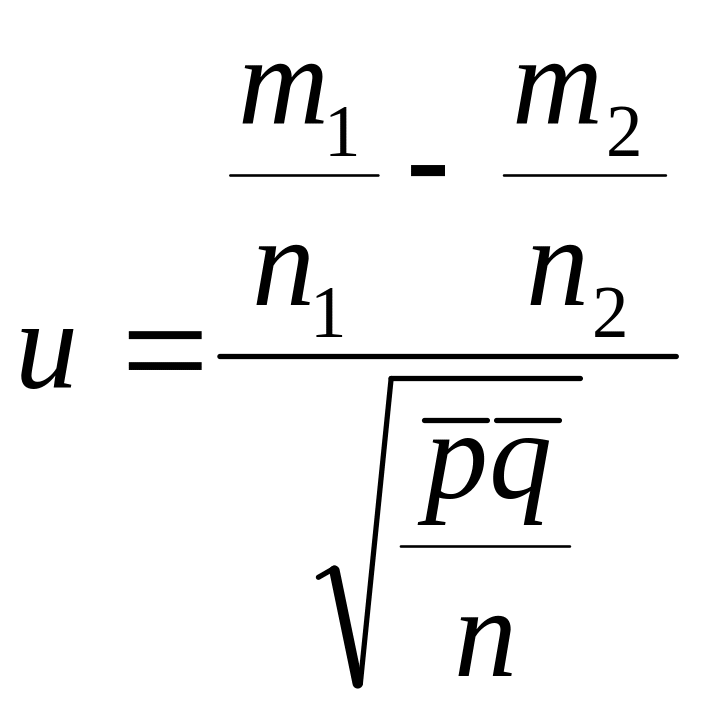
ma rozkład asymptotycznie normalny N ( 0,1 ) , We wzorze tym i są liczebnościami odpowiednio próby pierwszej i drugiej , i są liczbą elementów wyróżnionych odpowiednio w próbie pierwszej i drugiej , natomiast :

, ,

Parametryczne testy istotności – Przykłady

• test dla wartości średniej

Przykład 1. W celu sprawdzenia opinii, że średnie spożycie masła w czerwcu 2001 roku w rodzinach dwuosobowych wynosiło 1 kg , wybrano 300 rodzin dwuosobowych. Na podstawie uzyskanych informacji obliczono kg oraz kg . Przyjmijmy, że spożycie masła w populacji badanych rodzin ma skończoną wariancję i średnią . Sprawdźmy zatem wobec Na podstawie charakterystyk z próby należy obliczyć wartość statystyki u , która wynosi :

Ustalając  =0,05 , odczytujemy z tablic dystrybuanty rozkładu normalnego , przy czym spełnia relację . Ponieważ wartość 16,3268 znalazła się w zbiorze krytycznym , sprawdzaną hipotezę należy odrzucić na poziomie istotności =0,05 . Przyjmujemy więc głoszącą , że przeciętne spożycie masła w czerwcu 1992 roku w populacji badanych rodzin różniło się od wartości hipotetycznej wynoszącej 1 kg.

• test dla dwóch średnich

Przykład 2. W celu sprawdzenia przypuszczenia , że dzienne wydatki na pieczywo na osobę w rodzinach trzyosobowych w Rzeszowie są takie same jak w Łańcucie . Wylosowano z Rzeszowa 12 rodzin , a z Łańcuta 6. Zebrano odpowiednie informacje o wydatkach na pieczywo w listopadzie 2001 roku . Na podstawie zebranych danych obliczono dla :

Rzeszowa zł zł

Łańcuta zł zł

Przyjmuje się , że dzienne wydatki na pieczywo na osobę w rodzinach trzyosobowych w Rzeszowie i Łańcucie mają rozkład normalny o takiej samej wariancji.

Hipoteza zerowa jest następująca :

a alternatywna

Obliczona wartość statystyki zgodnie z wzorem wynosi t=0,796284. Z tablic rozkładu t-Studenta dla v=12 + 6 –2 stopni swobody i przyjętego poziomu istotności =0,05 , wartość krytyczna . Zatem nie ma podstaw do odrzucenia H₀ głoszącej , że średnie dzienne wydatki na pieczywo na osobę w rodzinach trzyosobowych Rzeszowa i Łańcuta są równe.

Test dla wskaźnika struktury - Przykład 3. W celu sprawdzenia przypuszczenia , że 30 % dorosłych ludzi w Polsce popiera obecne reformy , wybrano losowo 1200 dorosłych osób i zapytano je o akceptację aktualnych reform. Wśród wylosowanych 362 osoby wyraziły poparcie dla reform. Czy uzyskane wyniki potwierdzają nasze przypuszczenie ? Aby udzielić odpowiedzi na pytanie , formułujemy następujące hipotezy : oraz , a następnie obliczamy wartość statystyki u , zgodnie z wzorem , i otrzymujemy :

Przyjmując , odczytujemy z tablic rozkładu normalnego wartość krytyczną . Ponieważ wartość u =0,126 znajduje się w obszarze dopuszczalnym , nie mamy podstaw od odrzucenia sądu , że 30 % dorosłych osób w Polsce popiera aktualne reformy ( na poziomie istotności =0,06 )