
- •1 3(1) . Линейное программирование. Симплекс-метод. Привести числовой пример решения задачи линейного программирования симплекс-методом с использованием симплекс-таблиц.
- •2 3(3) . Свойства бинарных отношений. Рефлексивность, симметричность, транзитивность, иррефлексивность, антисимметричность, интранзитивность.
- •3 3(5) .Последовательная и связанная память. Представление линейных списков в последовательной и связанной памяти. Достоинства и недостатки того и другого представления
- •Логическое высказывание и его свойства. Логические операции (связки). Формализация логических суждений.
- •Машина Тьюринга, ее структура и свойства. Проблема остановки мт.
- •3 8(5) .Понятие обхода дерева. Виды обходов двоичного дерева. Определение структуры двоичного дерева по двум заданным обходам. Рекурсивные алгоритмы обходов двоичных деревьев.
- •1 16(1) . Цикломатика графов. Цикломатическое число. Цикломатический базис. Связь циклов графа с цикломатическим базисом.
- •2. Процессы в операционных системах. Общие понятия. Ресурсы процесса. Создание и уничтожение процесса.
- •3. Xml базы данных. Dtd и xml Schema
- •1 19(1) . Условная вероятность события. Формула полной вероятности и формула Байеса. Независимость событий (попарная и в совокупности). Примеры. Условная вероятность
- •Независимость событий
- •Формула полной вероятности
- •Теорема гипотез (формула Байеса)
- •2 19(4) . Логическое высказывание и его свойства. Логические операции (связки). Формализация логических суждений.
- •3 19(6) . Операционная система. Функции, назначение. Многопользовательские системы. Мультипрограммные системы.
- •1. Условная вероятность события. Формула полной вероятности и формула Байеса. Независимость событий (попарная и в совокупности).
- •1Нф (Первая Нормальная Форма)
- •2Нф (Вторая Нормальная Форма)
- •3Нф (Третья Нормальная Форма)
- •Алгоритм нормализации (приведение к 3нф)
- •К 43(6) лассы бинарных отношений. Отношение порядка и его свойства.
- •3 43(7) .Структура языка sql. Оператор select. Типы соединений таблиц.
Машина Тьюринга, ее структура и свойства. Проблема остановки мт.
Основная гипотеза теории алгоритмов (тезис Тьюринга) – всякий вычислительный процесс может быть преобразован в машину Тьюринга, всякий алгоритм – в таблицу такой машины.
Главное доказательство тезиса Тьюринга – никто и никогда не указал алгоритма, который нельзя было бы преобразовать в машину Тьюринга.
Сам Тьюринг получал свою машину путем анализа работы вычислителя: вычислитель имеет перед собой тетрадь, читает, пишет новые знаки, листает страницы, то есть работает по алгоритму, то есть работает память => ум вычислителя меняет свое состояние.
В машине Тьюринга процесс разложен на элементы(такты). Внутреннее состояние машины – состояние ума вычислителя. Машина Тьюринга – простейшая. Все другие машины и вычислительные модели отличаются от машин Тьюринга укрупнением операций (бегает по памяти, сразу читает и записывает и тп).
Итак, МТ- простейшая идеальная модель вычислительного процесса, а значит и простейшая идеальная вычислительная машина. Вычислительный процесс разложен на элементы. Так как внешняя память бесконечна, то машина не боится переполнения. Реальным машинам будет соответствовать машина Тьюринга с оборванной лентой.
МТ обрабатывает односторонне бесконечную ленту, Лента разбита на клетки, в которых пишутся символы по одному в клетке. Если в клетке ничего нет, то будем говорить, что там записан пустой символ. Множество знаков для ленты машины называется ее внешним алфавитом, в который входит и пустой знак. Внешний алфавит конечен. Машина имеет дискретное время работы. Оно распадается на такты. В каждый такт она занимает одну клетку ленты, читает записанный там символ, затем записывает новый символ, движется вправо или влево и переходит в следующее внутреннее состояние. Машина имеет конечное множество внутренних состояний (внутренний алфавит машины). Имеются начальное состояние (с него начинается работа машины) и конечное состояние, попав в которое, машина прекращает работу. Внутреннее состояние машины и воспринимаемый ею символ называется конфигурацией машины. Конфигурация машины однозначно определяет ее дальнейшие действия в этом такте: запись нового знака, движение, переход в следующее внутреннее состояние. Кроме ленты, имеется головкам чтения/записи, которая, во-первых, умеет двигаться вперед, назад и стоять на месте; во-вторых, умеет читать содержимое, стирать и записывать символы из данного алфавита; в третьих, управляется программой. Программа представляет собой таблицу, в которой в каждой клетке записана команда. Каждая клетка определяется двумя параметрами - символом алфавита и состоянием машины. Команда представляет собой указание, куда передвинуть головку чтения/записи из текущего состояния, какой символ записать в текущую ячейку и в какое состояние перейдет машина.
Более наглядной описание:
Машина Тьюринга состоит из следующих “частей” [2]:
ленты, разбитой на конечное число ячеек
Внешней памяти, принимающей одно из состояний, входящих в множество A={a0, a1, … am} . Ячейки ленты находятся в одном и только одном из состояний множества А. Состояние a0 называется пустым.
Внутренней памяти, принимающей одно из состояний, входящих в множество Q={q0, q1, … qm} . Состояние q0 называется “стоп”.
головки, двигающейся вдоль ленты и считывающей содержимое ячейки, напротив которой она останавливается.
Механического устройства, передвигающего головку и меняющего состояние внешней и внутренней памяти. Если головка с состоянии q стоит напротив ячейки с номером k, то изменения состояния внутренней памяти и состояния ячейки происходят одновременно.
8(3)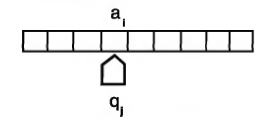
Рис1. Машина Тьюринга.
Работа машины Тьюринга осуществляется посредством команд, которые выполняет механическое устройство. Команда имеет один из следующих трех возможных видов:
qs ai -> qt aj
qs ai -> qt L
qs ai -> qt R
где L – это движение головки влево на одну ячейку, а R – вправо.
Смысл команды таков: если головка в состоянии qs обозревает ячейку в состоянии ai , то в первом случае она меняет свое состоянии на qt , а ячейки на aj , во втором случае - свое состоянии на qt и сдвигается влево, и в третьем – вправо.
Конечный набор команд образует команду.
Состояние машины – это последовательность состояний ai1, … air ячеек ленты, состояние внутренней памяти qs головки и номер k воспринимаемой ячейки в состоянии aik .
Машина Тьюринга работает на неограниченной с обеих сторон ленте, разделённой на ячейки, одну из которых обозревает головка. В любой момент времени все ячейки, кроме конечного числа, заняты пустыми символами. Конфигурацией машины Тьюринга m называется слово вида αqixβ, где - α и β непустая часть ленты, qi - текущее состояние управляющего устройства, x - обозреваемый головкой символ.
|
За каждый такт работы машины Тьюринга головка считывает обозреваемый символ с ленты и записывает на его место новый, при этом машина переходит в новое состяние qj или остаётся в старом, а головка передвигается на одну позицию влево или вправо, либо остаётся на месте. Порядок работы машины Тьюринга обычно записывается в виде таблицы, где в каждый столбец первой строки заносится возможное состояние машины Тьюринга qi Є Q, а в каждую строку первого столбца заносится символ внешнего алфавита x Є T. В других ячейках записываются команды исполняемые машиной Тьюринга в состоянии qi при обозревании символа x (ячейка пуста, если предполагается, что символ x не встречается в состоянии qi). Формат команды задаётся тройкой aKq, где а - символ печатаемый на ленте, К - направление движения головки из {L, R, S}, q - новое состояние машины Тьюринга. Рассмотрим программу сложения двух чисел заданных на ленте в унарной системе счисления для машины Тьюринга. Программа принимает 2 числа разделённых символом разделителя ('*'), и записывает результат их сложения на ленте сразу за этими числами отделяя его символом '='. Начальное состояние машины Тьюринга - q0, а головка обозревает первый символ первого числа. Конечное состояние - qz, при этом головка возвращается к исходной позиции. Программа перед своим завершением должна восстановить исходные данные на ленте.
8(4) |
|
Итак, внешний алфавит для решения данной задачи представляет из себя множество T = {λ, 1, 0, *, =}, а программа выглядит следующим образом:
Программа 1 - Программа сложения двух чисел в унарной системе для машины Тьюринга |
Как работает данная программа ? Достаточно просто. Она находит очередной символ '1' слагаемых, заменяет его на символ '0' (своеобразная пометка, что этот символ уже обработан) и записывает очередной символ '1' в результат. Затем головка возвращается к началу в поисках символа '0'. Если есть ещё символы '1' до символа '=', то повторяем предыдущий шаг, в противном случае - возвращаем головку в исходное состояние, восстанавливая на ленте входные данные (заменяем '0' на '1').
Проблема остановки машины Тьюринга.
На ленте произвольной машины Тьюринга записано произвольное начальное слово W. Остановится ли машина Т при работе с этим словом или нет?
В частных случаях этот вопрос решается легко. Например, если таблица машины Т не содержит команд с остановкой, или таблица машины Т состоит только из команд остановки.
Попробуем рассмотреть вопрос об общем алгоритме проверки машин Т на остановку.
Теорема1. Проблема остановки машины Т при данном начальном слове алгоритмически неразрешима.
Будем вести доказательство от противного. Пусть Т- машина Тьюринга, dТ- ее код ( таблица машины Т), W- начальное слово. Ввиду второй теоремы Шеннона мы можем ограничиться вопросом об остановке двусимвольных машин Тьюринга. Предположим, что существует машина Е, решающая проблемы остановки машины Т. На ленте машины Е кодовое число машины Т и начальное слово W. Машина Е работает и печатает «+» если машины Т останавливается, и «-» в противном случае. Пусть W=dТ. В этом случае можно сказать, что машина Т занимается самоанализом. Всякая ли машина способна заниматься самоанализом? В принципе, всякая, если ее внешний алфавит включает все символы ее таблицы, то машина может самоанализировать. Ясно, что таблицу можно расширить: в незнакомой ситуации машина останавливается => всякая машина Тьюринга может заниматься самоанализом. Построим машину D для проверки на остановку самоанализирующих машин Тьюринга (когда W=dT), то есть проверяющую останавливается ли машина при самоанализе. Машину D получим следующим образом : сначала D копирует на ленту dT, а потом работает как машина E. Если мы умеем строить машину Е, то построим и машину D. Теперь преобразуем машину D в машину С, которая работает так же как и машина D вплоть до остановки машины D, но если при слове dT машина D печатает «+» и останавливается, то машина C печатает «+» и не останавливается, а двигается по ленте неограниченно вправо (не меняя никаких знаков).
машина D => машина С и тк машина D => машина Е, то машина С машина Е. Итак, машина С не останавливается, если Т останавливается и машина С останавливается, если машина Т не останавливается. Пусть теперь Т=С, то есть машина С занимается самоанализом. Тогда машина С остановится, если машина С не остановится, и машина С не остановится, если машина С остановится. Отсюда противоречие => наша задача алгоритмически неразрешима.

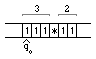
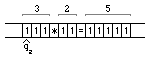 Рисунок
3 - Пример конечного состояния машины
Тьюринга
Рисунок
3 - Пример конечного состояния машины
Тьюринга