1. Логическое высказывание и его свойства. Логические операции (связки). Формализация логических суждений.

Высказывание – всякое утверждение или отрицание.

Принцип экзистенциональности (объёма): мы отвлекаемся от содержания высказывания и рассмотрение только значения истинности. Есть два значения истинности: ложь и истина. В алгебраической системе обозначений (Буль) 0 – ложь, 1 – истина. В собственно логической системе обозначений (Пеано и Рассел) ٨ – ложь, ٧ – истина.

Высказывательная функция ­­– это функция, определённая на значениях истинности и принимающая значения истинности. Эта функция задаёт логическое высказывание.

Основные логические операции:

1. Дизъюнкция (булево сложение). 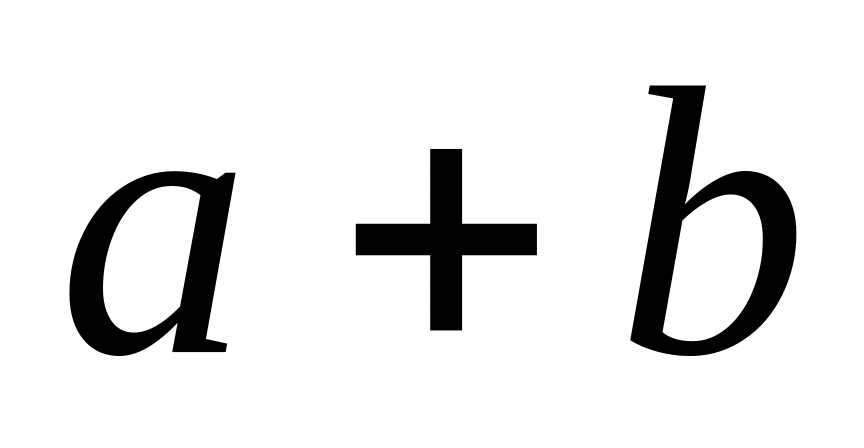. В естественном языке дизъюнкция интерпретируется как ИЛИ (И).

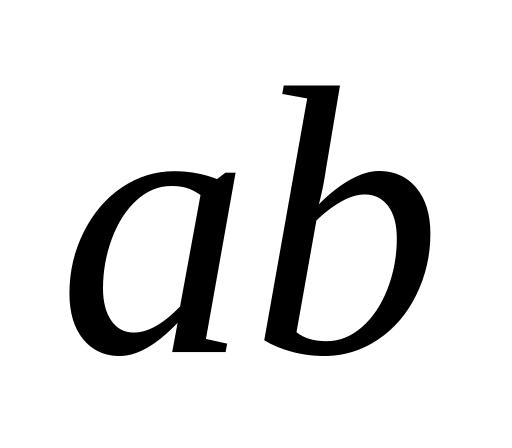2. Конъюнкция (булево умножение). . В естественном языке конъюнкция интерпретируется как И.

3. Отрицание. . НЕ.

4. Следование (импликация). .

5. Эквивалентность (тождество) .

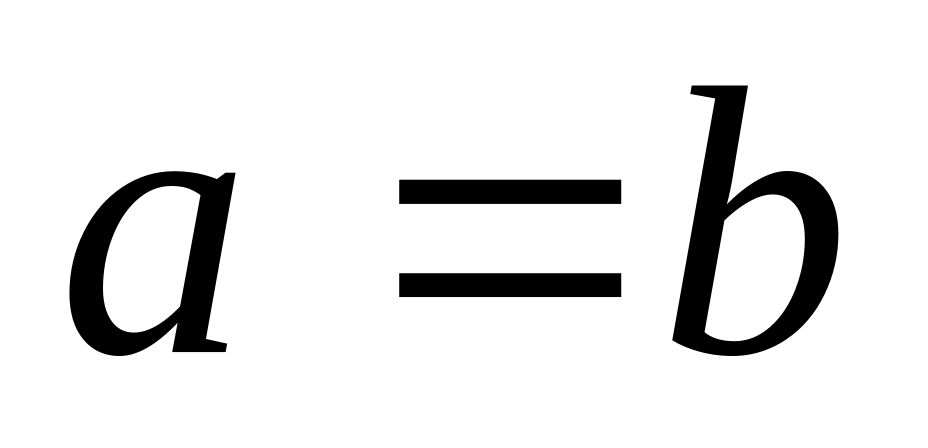6. Неравенства: .

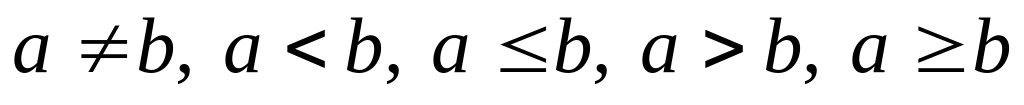Простые логические высказывания – это константы 0 и 1, а также переменные. Сложные высказывания образуются из простых с помощью логических связок (операций) и знаков пунктуации (скобок). Значения логического высказывания характеризуются его таблицей истинности. При составлении таблицы истинности осуществляется полный перебор всех комбинаций значений переменных, входящих в высказывание и для каждой комбинации вычисляется значение истинности высказывания.

Таблицы истинности основных логических операций:

1. a	b	ab
   0	0	0
   0	1	0
   1	0	0
   1	1	1

   Дизъюнкция 2)Конъюнкция

a	b		a+b
0	0		0
0	1		1
1	0		1
1	1		1

0	1
1	0

a	b	a=b
0	0	1
0	1	0
1	0	0
1	1	1

a	b	a=>b
0	0	1
0	1	1
1	0	0
1	1	1

3)Следование 4)Отрицание 5)Эквивалентность

С помощью таблицы истинности можно решать логические задачи. Пример: доказать, что . Проверим равенство с помощью таблицы истинности.

0	0
0	1
1	0
1	1

При всех комбинациях переменных и выражение истинно. Следовательно, выражения и равны.

8(2)