2 3(3) . Свойства бинарных отношений. Рефлексивность, симметричность, транзитивность, иррефлексивность, антисимметричность, интранзитивность.

Декартовым произведением двух множеств А и В является новое множество С, элементами которого являются все пары (a,b), . Порядок в паре очень важен, в общем виде .

Бинарным отношением Т(М) на множестве М называется подмножество , . Довольно часто используется другая, инфексная форма записи бинарного отношения a T b = . Бинарное отношение T(M) называется рефлексивным тогда и только тогда, когда для каждого элемента пара (х,х) принадлежит этому бинарному отношению, т.е. . Для определения этого свойства множество М должно содержать хотя бы один элемент х.

Бинарное отношение T(M) называется иррефлексивным тогда и только тогда, когда для каждого элемента пара (х, х) не принадлежит этому бинарному отношению, т.е. .

Если бинарное отношение T(M) не обладает ни свойством рефлексивности, ни свойством иррефлексивности, то оно является нерефлексивным.

Cвойство рефлексивности определяется для непустых множеств! В соответствии с этим, бинарное отношение на пустом множестве , является нерефлексивным. Также нерефлексивно пустое бинарное отношение.

Рассмотрим множество M={a,b,c,d}. Ниже приведены примеры рефлексивных, иррефлексивных и нерефлексивных бинарных отношений.

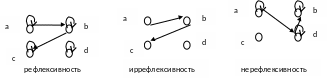
При матричном задании бинарного отношения, отношение рефлексивно, если на главной диагонали стоят единицы. Если на главной диагонали стоят нули, то отношение является иррефлексивным. Если на главной диагонали стоят как «1» так и «0» то отношение нерефлексивно.

Рефлексивно				Иррефлексивно				Нерефлексивно
	a	b	c		a	b	c		a	b	c
a	1	0	0	a	0	0	1	A	1	1	0
b	0	1	1	b	0	0	1	B	1	0	1
c	1	0	1	c	1	1	0	C	0	0	1

Бинарное отношение T(M) называется симметричным тогда и только тогда, когда для каждой пары (х, у) , обратная пара (у, х) также принадлежит этому бинарному отношению, т.е. . Для определения этого свойства множество М должно содержать хотя бы два различных элемента х и у.

Бинарное отношение T(M) называется антисимметричным тогда и только тогда, когда из того, что следует, что .

Е

3(4)

сли бинарное отношение T(M) не обладает ни свойством симметричности, ни свойством антисимметричности, то оно является несимметричным.

Cвойство симметричности определяется для непустых множеств! В соответствии с этим, бинарные отношения на пустом множестве , так же как на множествах с одним элементом, является несимметричными.

Рассмотрим множество M={a,b,c,d}. На рис.5 приведены примеры рефлексивных, иррефлексивных и нерефлексивных бинарных отношений.

При матричном задании отношения, если отношение симметрично, то матрица отношения симметричная. Если отношение антисимметрично, то .

Свойство транзитивности определяется на трех различных элементах множества М. Бинарное отношение T(M) называется транзитивным тогда и только тогда, когда для каждых двух пар элементов (х, у) и (у ,z), принадлежащих бинарному отношению , пара (x, z) также принадлежит этому бинарному отношению, т.е. . При графическом представлении транзитивного бинарного отношения (рис. 6) можно увидеть спрямление пути длины два (х, у) (у ,z), между двумя элементами, т.е. транзитивное замыкание («транзит») между x и z.

Бинарное отношение T(M) называется интранзитивным тогда и только тогда, когда для каждых двух пар элементов (х, у) и (у ,z), принадлежащих бинарному отношению , пара (x, z) не принадлежит этому бинарному отношению, т.е. . При графическом представлении интранзитивного бинарного отношения (рис. 7) можно увидеть, что ни один имеющийся путей не обладает транзитивным замыканием!

Если бинарное отношение T(M) не обладает ни свойством транзитивности, ни свойством интранзитивности, то оно является нетранзитивным.

Бинарные отношения на пустом множестве , на множествах с одним элементом M1={a} или двумя элементами M2={a,b} является нетранзитивными.