
- •1 3(1) . Линейное программирование. Симплекс-метод. Привести числовой пример решения задачи линейного программирования симплекс-методом с использованием симплекс-таблиц.
- •2 3(3) . Свойства бинарных отношений. Рефлексивность, симметричность, транзитивность, иррефлексивность, антисимметричность, интранзитивность.
- •3 3(5) .Последовательная и связанная память. Представление линейных списков в последовательной и связанной памяти. Достоинства и недостатки того и другого представления
- •Логическое высказывание и его свойства. Логические операции (связки). Формализация логических суждений.
- •Машина Тьюринга, ее структура и свойства. Проблема остановки мт.
- •3 8(5) .Понятие обхода дерева. Виды обходов двоичного дерева. Определение структуры двоичного дерева по двум заданным обходам. Рекурсивные алгоритмы обходов двоичных деревьев.
- •1 16(1) . Цикломатика графов. Цикломатическое число. Цикломатический базис. Связь циклов графа с цикломатическим базисом.
- •2. Процессы в операционных системах. Общие понятия. Ресурсы процесса. Создание и уничтожение процесса.
- •3. Xml базы данных. Dtd и xml Schema
- •1 19(1) . Условная вероятность события. Формула полной вероятности и формула Байеса. Независимость событий (попарная и в совокупности). Примеры. Условная вероятность
- •Независимость событий
- •Формула полной вероятности
- •Теорема гипотез (формула Байеса)
- •2 19(4) . Логическое высказывание и его свойства. Логические операции (связки). Формализация логических суждений.
- •3 19(6) . Операционная система. Функции, назначение. Многопользовательские системы. Мультипрограммные системы.
- •1. Условная вероятность события. Формула полной вероятности и формула Байеса. Независимость событий (попарная и в совокупности).
- •1Нф (Первая Нормальная Форма)
- •2Нф (Вторая Нормальная Форма)
- •3Нф (Третья Нормальная Форма)
- •Алгоритм нормализации (приведение к 3нф)
- •К 43(6) лассы бинарных отношений. Отношение порядка и его свойства.
- •3 43(7) .Структура языка sql. Оператор select. Типы соединений таблиц.
1Нф (Первая Нормальная Форма)
Понятие первой нормальной формы уже обсуждалось в главе 2. Первая нормальная форма (1НФ) – это обычное отношение. Согласно нашему определению отношений, любое отношение автоматически уже находится в 1НФ. Напомним кратко свойства отношений (это и будут свойства 1НФ):
1.В отношении нет одинаковых кортежей.
2.Кортежи не упорядочены.
3.Атрибуты не упорядочены и различаются по наименованию.
4.Все значения атрибутов атомарны.
2Нф (Вторая Нормальная Форма)
Определение 3.
Отношение
![]() находится
во второй
нормальной форме
(2НФ)
тогда и только тогда, когда отношение
находится в 1НФ и нет
неключевых атрибутов, зависящих от
части сложного ключа.
(Неключевой
атрибут
- это атрибут, не входящий в состав
никакого потенциального ключа).
находится
во второй
нормальной форме
(2НФ)
тогда и только тогда, когда отношение
находится в 1НФ и нет
неключевых атрибутов, зависящих от
части сложного ключа.
(Неключевой
атрибут
- это атрибут, не входящий в состав
никакого потенциального ключа).
Замечание. Если потенциальный ключ отношения является простым, то отношение автоматически находится в 2НФ. Для того, чтобы устранить зависимость атрибутов от части сложного ключа, нужно произвести декомпозицию отношения на несколько отношений. При этом те атрибуты, которые зависят от части сложного ключа, выносятся в отдельное отношение.
3Нф (Третья Нормальная Форма)
Определение 4. Атрибуты называются взаимно независимыми, если ни один из них не является функционально зависимым от другого.
Определение 5. Отношение находится в третьей нормальной форме (3НФ) тогда и только тогда, когда отношение находится в 2НФ и все неключевые атрибуты взаимно независимы.
Для того, чтобы устранить зависимость неключевых атрибутов, нужно произвести декомпозицию отношения на несколько отношений. При этом те неключевые атрибуты, которые являются зависимыми, выносятся в отдельное отношение.
Алгоритм нормализации (приведение к 3нф)
Итак, алгоритм нормализации (т.е. алгоритм приведения отношений к 3НФ) описывается следующим образом.
Шаг 1 (Приведение к 1НФ). На первом шаге задается одно или несколько отношений, отображающих понятия предметной области. По модели предметной области (не по внешнему виду полученных отношений!) выписываются обнаруженные функциональные зависимости. Все отношения автоматически находятся в 1НФ.
Шаг 2 (Приведение
к 2НФ). Если
в некоторых отношениях обнаружена
зависимость атрибутов от части сложного
ключа, то проводим декомпозицию этих
отношений на несколько отношений
следующим образом: те атрибуты, которые
зависят от части сложного ключа выносятся
в отдельное отношение вместе с этой
частью ключа. В исходном отношении
остаются все ключевые атрибуты: Исходное
отношение:
![]() .
Ключ:
.
Ключ:
![]() -
сложный. Функциональные зависимости:
-
сложный. Функциональные зависимости:
![]() -
зависимость всех атрибутов от ключа
отношения.
-
зависимость всех атрибутов от ключа
отношения.
![]() -
зависимость некоторых атрибутов от
части сложного ключа.
-
зависимость некоторых атрибутов от
части сложного ключа.
Декомпозированные
отношения:
![]() -
остаток от исходного отношения. Ключ
.
-
остаток от исходного отношения. Ключ
.
![]() -
атрибуты, вынесенные из исходного
отношения вместе с частью сложного
ключа. Ключ
-
атрибуты, вынесенные из исходного
отношения вместе с частью сложного
ключа. Ключ
![]() .
.
Шаг 3 (Приведение к 3НФ). Если в некоторых отношениях обнаружена зависимость некоторых неключевых атрибутов других неключевых атрибутов, то проводим декомпозицию этих отношений следующим образом: те неключевые атрибуты, которые зависят других неключевых атрибутов выносятся в отдельное отношение. В новом отношении ключом становится детерминант функциональной зависимости:
Исходное отношение:
![]() .
Ключ:
.
Ключ:
![]() .
.
Функциональные
зависимости:
![]() -
зависимость всех атрибутов от ключа
отношения.
-
зависимость всех атрибутов от ключа
отношения.
![]() -
зависимость некоторых неключевых
атрибутов других неключевых атрибутов.
-
зависимость некоторых неключевых
атрибутов других неключевых атрибутов.
Декомпозированные
отношения:
![]() -
остаток от исходного отношения. Ключ
.
-
остаток от исходного отношения. Ключ
.
![]() -
атрибуты, вынесенные из исходного
отношения вместе с детерминантом
функциональной зависимости. Ключ
-
атрибуты, вынесенные из исходного
отношения вместе с детерминантом
функциональной зависимости. Ключ
![]() .
.
Таблица находится в третьей нормальной форме Бойса-Кодда (НФБК) (усиленная третья нормальная форма) тогда и только тогда, когда любая функциональная зависимость между ее атрибутами сводится к полной функциональной зависимости от возможного первичного ключа (т.е. все детерминанты отношения являются потенциальными первичными ключами).
Пример: Экзамен(№ Зач. Книжки, Дисциплина, День сдачи, Время сдачи, Преподаватель, Оценка).
PK1= № Зач. Книжки, Дисциплина. // Потенциальные первичные ключи
PK2= День сдачи, Время сдачи, Преподаватель.
PK3=№ Зач. Книжки, День сдачи.
Дисциплина(День сдачи, Преподаватель).
Расписание(День сдачи, Преподаватель, Дисциплина).
М
43(1)
Метод исключения Гаусса относится к числу точных методов решения систем линейных уравнений (метод решения задачи относят к классу точных, если в предположении отсутствия округлений он дает точное решение задачи после конечного числа арифметических и логических операций).
Схема единственного деления
Пусть дана система уравнений
|
(1) |
где
![]() – матрица размерности
– матрица размерности
![]() ,
,
![]() ,
,
![]() .
.
В предположении,
что
![]() ,
первое уравнение системы
,
первое уравнение системы
|
(2) |
делим на коэффициент
![]() ,
в результате получаем уравнение
,
в результате получаем уравнение
|
Затем из каждого
из остальных уравнений вычитается
первое уравнение, умноженное на
соответствующий коэффициент
![]() .
В результате эти уравнения преобразуются
к виду
.
В результате эти уравнения преобразуются
к виду
|
Первое неизвестное
оказалось исключенным из всех уравнений,
кроме первого. Далее в предположении,
что
![]() ,
делим второе уравнение на коэффициент
,
делим второе уравнение на коэффициент
![]() и исключаем неизвестное
и исключаем неизвестное
![]() из всех уравнений, начиная со второго,
и т.д. Продолжая процесс исключения
неизвестных и считая, что возможны все
шаги до m-го
включительно, получим
из всех уравнений, начиная со второго,
и т.д. Продолжая процесс исключения
неизвестных и считая, что возможны все
шаги до m-го
включительно, получим
|
(3) |
где

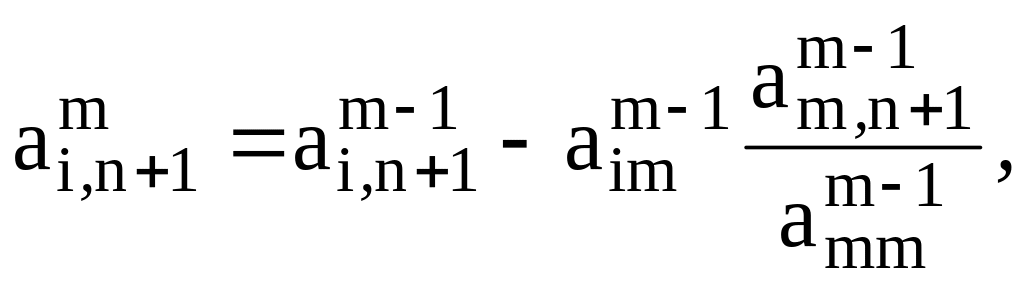
![]() .
.
Предположим, что шаг номера m есть последний возможный шаг преобразований. Возможны два случая: m=n и m<n. Если m=n, то это означает, что после преобразований мы получим систему вида
|
(4) |
с треугольной
матрицей, эквивалентной исходной
системе. Из системы (4) значения для
неизвестных находим последовательно
от
![]() к
к
![]() по формулам
по формулам
|
(5) |
Процесс нахождения коэффициентов треугольной системы (4) называется прямым ходом, а процесс получения ее решения по формулам (5) – обратным ходом метода Гаусса.
П
43(2)![]() равны нулю и уравнения имеют вид
равны нулю и уравнения имеют вид
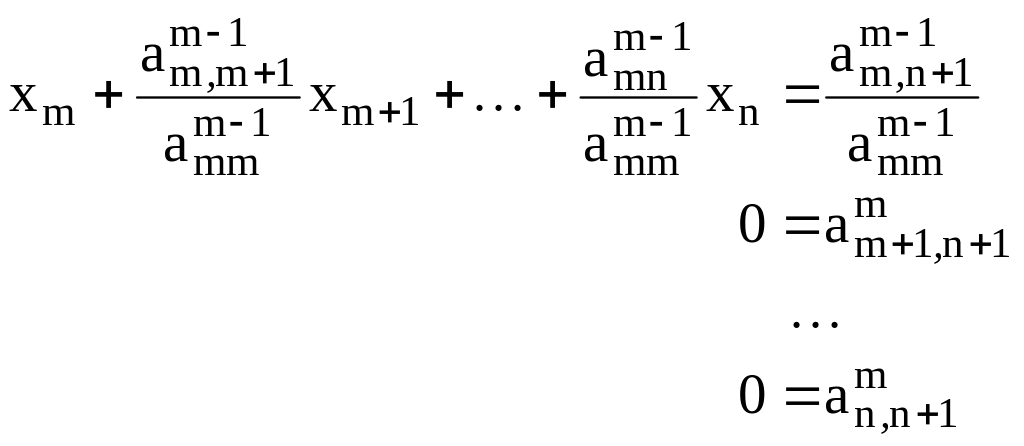
Если свободные
члены
![]() все равны нулю, то получим только одно
первое уравнение. Объединив первые
уравнения всех шагов до m-го
включительно, мы получим систему вида
все равны нулю, то получим только одно
первое уравнение. Объединив первые
уравнения всех шагов до m-го
включительно, мы получим систему вида
|
из которой можем
найти выражения неизвестных
![]() через неизвестные
через неизвестные
![]() и свободные члены. В этом случае система
(1) имеет бесчисленное множество решений.
и свободные члены. В этом случае система
(1) имеет бесчисленное множество решений.
Если m<n
и хотя бы одно
![]() ,
то система (1) несовместна.
,
то система (1) несовместна.
Реализация прямого
хода метода Гаусса требует
![]() арифметических операций, а обратного
–
арифметических операций, а обратного
–
![]() арифметических операций.
арифметических операций.
Примечание1 Подсчет числа выполняемых арифметических действий.
Лемма1. Выполняются равенства
|
|
∆: Первое равенство, выражающее сумму арифметической прогрессии, очевидно. Докажем с помощью метода математической индукции. Второе равенство выполняется при n=1. Допустим, что оно верно при некотором натуральном n=m. Тогда
![]() .
.
Следовательно, по индукции второе равенство верно для любого натурального n. □
Подсчитаем количество выполняемых арифметических действий при решении системы порядка n. При исключении неизвестной осуществляются следующие действия:
а) производится всего n делений второго и следующих коэффициентов первого уравнения и его правой части на коэффициент при ;
б) расходуется по n умножений и n вычитаний при исключении из второго и последующих уравнений, число которых равно n-1.
Таким образом, общее число арифметических действий, затрачиваемых на исключение , имеет величину
|
(5.1) |
При исключении
производятся совершенно аналогичные
вычисления, как и при исключении
.
Разница состоит лишь в том, что
осуществляются действия над строками
матрицы, размеры которой в каждом
направлении на единицу меньше. Поэтому
число выполняемых арифметических
действий
![]() при исключении
получается из выражения (5.1) заменой n
на n–1:
при исключении
получается из выражения (5.1) заменой n
на n–1:
![]() .
.
Вообще, при
исключении неизвестной
![]() выполняются
выполняются
![]() арифметических действий:
арифметических действий:
![]() .
.
43(3)
![]() .
.
Отсюда, полагая k
= n
– i+1
и применяя лемму 1, находим явное выражение
для
![]() :
:
|
(5.2) |
В обратном ходе число умножений и вычитаний, вместе взятых, равно удвоенному числу элементов квадратной матрицы порядка n, расположенных под главной диагональю, и, как показывают подсчеты, составляет величину
|
(5.3) |
Итак, число арифметических действий, выполняемых при решении системы линейных алгебраических уравнений порядка n методом Гаусса, в общем случае равно
|
(5.4) |
Примечание 2 Другая реализация схемы единственного деления
Исключение происходит в результате следующих операций:
а) деление i-го
уравнения на
![]() ;
;
б) вычитания
получившегося после такого деления
i-го
уравнения, умноженного на
![]() ,
из уравнений с номерами k
= i
+ 1,…,
n.
Первая операция равносильна умножению
системы уравнений слева на диагональную
матрицу
,
из уравнений с номерами k
= i
+ 1,…,
n.
Первая операция равносильна умножению
системы уравнений слева на диагональную
матрицу
 ;
;
вторая операция равносильна умножению слева на матрицу
 .
.
Таким образом, система (3), получаемая в результате этих преобразований, запишется в виде:
![]() ,
где
,
где
![]() .
.
Произведение левых (правых) треугольных матриц является левой (правой) треугольной матрицей, поэтому матрица С левая треугольная.
Из формулы для элементов обратной матрицы
![]()
следует, что
матрица, обратная к левой (правой)
треугольной, является левой (правой)
треугольной. Следовательно, матрица
![]() левая треугольная.
левая треугольная.
Введем обозначение
![]() .
Согласно построению все
.
Согласно построению все
![]() и матрица D
правая треугольная. Отсюда получаем
представление матрицы A
в виде произведения левой и правой
треугольных матриц:
и матрица D
правая треугольная. Отсюда получаем
представление матрицы A
в виде произведения левой и правой
треугольных матриц:
![]() .
.
43(4)![]() вместе с условием
вместе с условием
![]() образует систему уравнений относительно
элементов треугольных матриц B
и D:
образует систему уравнений относительно
элементов треугольных матриц B
и D:
![]() .
.
Поскольку
![]() при i
< j
и
при i
< j
и
![]() при k
< j,
эта система может быть записана
в виде:
при k
< j,
эта система может быть записана
в виде:
|
(6) |
или, что то же самое,
|
|
Воспользовавшись
условием, что все
,
получаем систему рекуррентных соотношений
для определения элементов
![]() и
и
![]() :
:
|
(7) |
|
Вычисления
проводятся последовательно для
совокупностей
![]() .
Здесь и далее в случае, когда верхний
предел суммирования меньше нижнего,
считается, что вся сумма равна нулю.
.
Здесь и далее в случае, когда верхний
предел суммирования меньше нижнего,
считается, что вся сумма равна нулю.
Таким образом,
вместо последовательных преобразований
системы (2) к виду (3) можно непосредственно
произвести вычисление матриц B
и D
с помощью формул (7). Эти вычисления можно
осуществить, только если все элементы
![]() окажутся отличными от нуля. Пусть
окажутся отличными от нуля. Пусть
![]() –
матрицы главных миноров k-го
порядка матриц A,
B,
D.
Согласно (6)
–
матрицы главных миноров k-го
порядка матриц A,
B,
D.
Согласно (6)
![]() .
Поскольку
.
Поскольку
![]() ,
то
,
то
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Итак, для осуществимости вычислений по формулам (7) необходимо и достаточно выполнение условий
![]() .
.
Возможен вариант,
когда все
,
но среди величин
![]() есть очень малые и при делении на них
будут получаться большие числа с большими
абсолютными погрешностями. В результате
этого решение сильно исказится.
есть очень малые и при делении на них
будут получаться большие числа с большими
абсолютными погрешностями. В результате
этого решение сильно исказится.
Введем обозначение
![]() .
Поскольку
.
Поскольку
![]() и
,
то справедливы равенства
и
,
то справедливы равенства
![]() ,
,
![]() .
Таким образом, после разложения матрицы
исходной системы на произведение левой
и правой треугольных матриц решение
исходной системы сводится к последовательному
решению двух систем
.
Таким образом, после разложения матрицы
исходной системы на произведение левой
и правой треугольных матриц решение
исходной системы сводится к последовательному
решению двух систем
![]() с треугольными матрицами; это потребует
с треугольными матрицами; это потребует
![]() арифметических операций.
арифметических операций.
Последовательность
операций по разложению матрицы A
на произведение треугольных матриц и
по определению вектора
![]() часто удобно объединить. Уравнения
часто удобно объединить. Уравнения
![]()
системы можно записать в виде (6)
![]() .
.
С
43(5)![]() могут вычисляться одновременно с
остальными значениями
могут вычисляться одновременно с
остальными значениями
![]() по формулам (7).
по формулам (7).
Метод Гаусса с выбором главного элемента
Его применяют для того, чтобы избежать катастрофического влияния вычислительной погрешности. Пусть по ходу исключения неизвестных получена система уравнений
|
|
Найдем
![]() такое, что
такое, что
![]() и переобозначим
и переобозначим
![]() и
и
![]() ;
далее произведем исключение неизвестной
;
далее произведем исключение неизвестной
![]() из всех уравнений, начиная с (k
+ 2)-го. Такое
переобозначение приводит к изменению
порядка исключения неизвестных и во
многих случаях уменьшает чувствительность
решения к погрешностям округления при
вычислениях.
из всех уравнений, начиная с (k
+ 2)-го. Такое
переобозначение приводит к изменению
порядка исключения неизвестных и во
многих случаях уменьшает чувствительность
решения к погрешностям округления при
вычислениях.
Примечание
3 Число выполняемых арифметических
действий над правыми частями уравнений
в прямом ходе метода Гаусса.
При исключении
правая часть первого уравнения делится
на коэффициент при
,
а при нахождении правых частей остальных
уравнений производится по одному
умножению и одному вычитанию. Таким
образом, при исключении
всего над правыми частями выполняется
![]() арифметических действий:
арифметических действий:
![]() .
.
Соответственно,
с правыми частями уравнений при исключении
осуществляется
![]() арифметических действий:
арифметических действий:
![]() .
.
Следовательно, в прямом ходе число выполняемых арифметических действий над правыми частями уравнений имеет величину
|
(7.1) |
Примечание 4 Решение нескольких систем, отличающихся правыми частями
Часто требуется
решить несколько систем уравнений
![]() с одной и той же матрицей A.
Удобно поступить следующим образом:
введя обозначения
с одной и той же матрицей A.
Удобно поступить следующим образом:
введя обозначения
![]()
произведем
вычисления по формулам (7), причем элементы
![]() вычислим при
вычислим при
![]() .
В результате будут получены p
систем уравнений с треугольной матрицей,
соответствующих истинной задаче
.
В результате будут получены p
систем уравнений с треугольной матрицей,
соответствующих истинной задаче
![]() .
.
Решаем эти системы каждую в отдельности. Обратный ход для нахождения решения каждой системы проводится последовательно.
Число арифметических действий при решении p указанных систем согласно (5.3), (5.4) и (7.1) составляет величину
|
где Q
– число действий при полном решении
одной системы,
![]() – число действий в прямом ходе над одним
столбцом правых частей,
– число действий в прямом ходе над одним
столбцом правых частей,
![]() –
число действий в обратном ходе при
нахождении одного решения.
–
число действий в обратном ходе при
нахождении одного решения.

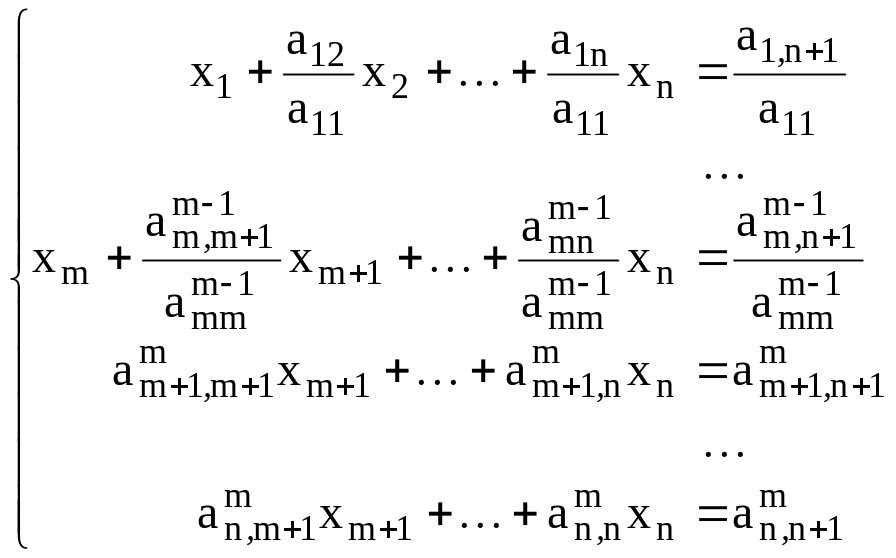
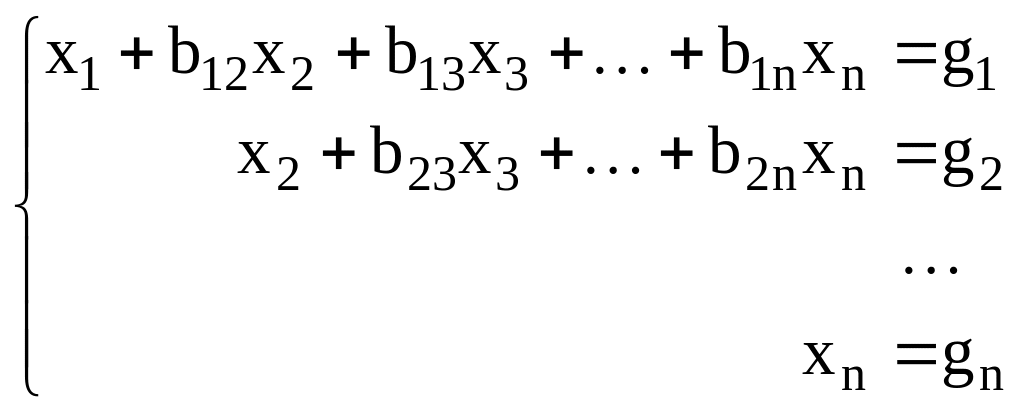
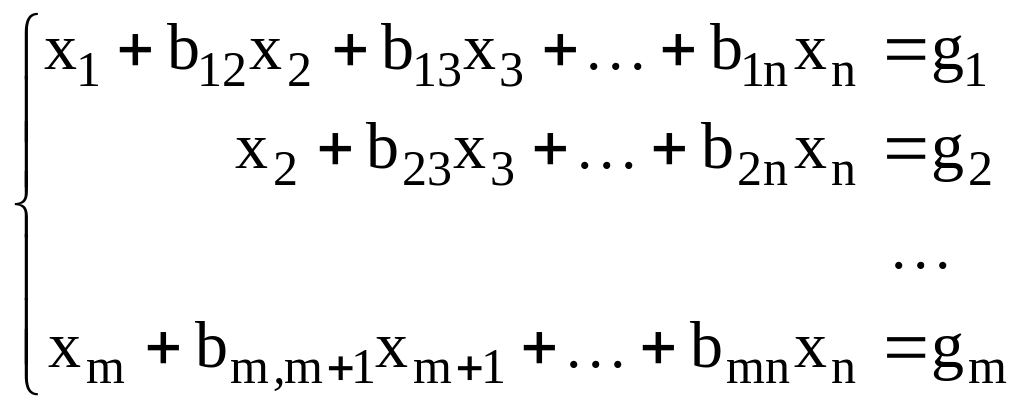
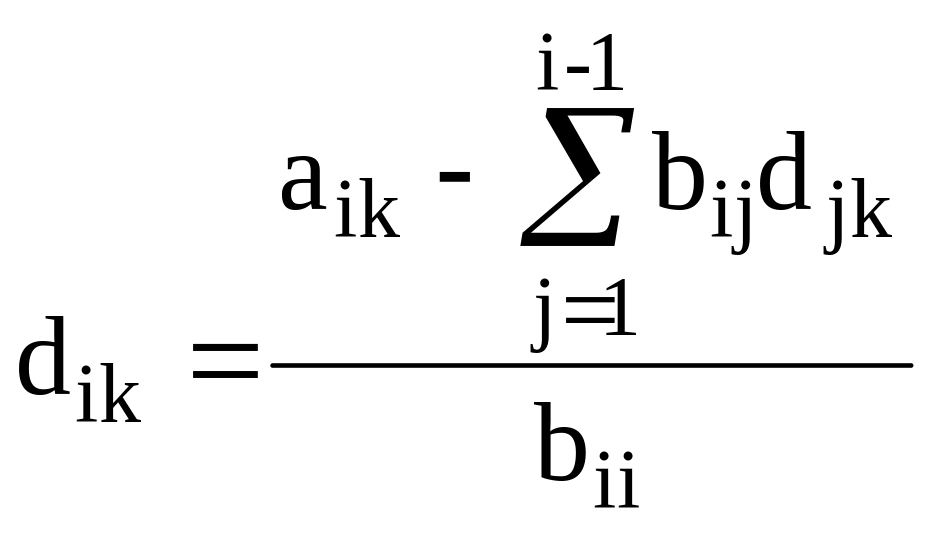 при
.
при
.