3 19(6) . Операционная система. Функции, назначение. Многопользовательские системы. Мультипрограммные системы.

Операционная система – программный комплекс, предоставляющий пользователю средства для выполнения прикладных программ и управления ими, а также обеспечивающий средства доступа прикладных программ к аппаратным ресурсам и средства управления ими – распределение оперативной памяти, процессорного времени, доступ к файлам и периферийным устройствам. Программы пользователя рассматриваются ОС как процессы – именованные области памяти, содержащие выполняемый код, данные и описательную информацию о своем окружении. Ядро типичной ОС (на примере UNIX) имеет следующую структуру:

Прикладные программы

↨Интерфейс системных вызовов

↨ ↨Файловая система <-> Система управления процессами

↨ ↑Система ввода-вывода │

↨ ↓ Драйверы

↨Аппаратное обеспечение

ОС можно классифицировать по следующему набору признаков:

По количеству обслуживаемых пользователей:

1. Однопользовательские – в один момент времени в системе работает не более одного пользователя, не делается никаких различий между пользователями – все они имеют доступ ко всем ресурсам, предоставляемым ОС

2. Многопользовательские – пользователи, использующие систему, различимы, могут работать в системе либо параллельно, либо не более одного в один момент времени. В таких системах существует необходимость в механизмах идентификации и аутентификации пользователей (например, по учетному имени и паролю), раздельному хранению данных и программ пользователей (например, в домашних каталогах). В таких системах применяются средства разграничения доступа на уровне пользователей – определение привилегий, дающих права доступа к файлам. По количеству одновременно выполняемых программ пользователя: 1)Однопрограммные – в один момент времени в системе запущена только одна программа пользователя, получающая полный доступ ко всем ресурсам, предоставляемым ОС. 2)Многопрограммные – в один момент времени в системе может быть запущено много программ (процессов). В этом случае в состав ядра ОС должен входить планировщик процессов, выполняющий следующие функции: a.Создание и удаление процессов; b.Распределение системных ресурсов (процессорного времени, памяти) между процессами; c.Синхронизация процессов; d.Межпроцессное взаимодействие. Также в таких ОС усложняется система ввода-вывода, т.к. один файл или устройство может использоваться совместно несколькими процессами. Для предотвращения конфликтов используются блокировки, разрешающие доступ к ресурсу только одному процессу в один момент времени.

41(1)

1. Условная вероятность события. Формула полной вероятности и формула Байеса. Независимость событий (попарная и в совокупности).

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет. Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А|В) или P_B(A). Условная вероятность события А при условии наступления события В равна Р(А|В)= Р(АB) /P(B) , эта формула называется формулой условной вероятности. Говорят, что событие А независимо от события В, если имеет место равенство: Р(А|В)= Р(А), т.е. если наступление события В не меняет вероятности события А. а условие зависимости: Р(А|В)  Р(А).

Теорема умножения: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место: P(AB) = P(A)P(B|A).Доказательство:Пусть возможные исходы опыта сводятся кn элементарным событиям.Предположим, что событию A благоприятны m элементарных событий, а событию B благоприятны k элементарных событий. Так как мы не предполагали события А и В несовместными, то вообще существуют элементарные события, благоприятные и событию А, и событию В одновременно. Пусть число таких элементарных событий l. Тогда P(AB) = l / n ,, P(A) = m / n Вычислим P(B|A), т.е. условную вероятность события В в предположении, что А имело место. Если известно, что событие А произошло, то из ранее возможныхn элементарных событий остаются возможными только m, которые благоприятствовали событию А. Из них l элементарных событий благоприятны событию В. Следовательно, P(B|A) = l / m. Подставим полученные выражения в P(AB)=P(A)P(B|A) l /n =( m / n)  (l / m). Получили тождество. Теорема доказана. Следствие 1 Если событие А не зависит от события В, то и событие В не зависит от события А. Доказательство: Дано, что событие А не зависит от события В, т.е. P(A) = P(A|B), Требуется доказать, что и событие В не зависит от А, т.е. P(B) = P(B|A), При доказательстве будем предполагать, что P(A) 0. Напишем теорему вероятностей в двух формах: P(AB)=P(B)P(A|B), P(AB)=P(A)P(B|A). Откуда P (A)P(B|A)=P(B)P(A|B) Или так как событие А не зависит от В, т.е. P(A) = P(A|B), то P(A)P(B|A)=P(B)P(A). Разделим обе части равенства на P(A). Получим: P(B|A)=P(B). Что и требовалось доказать.

Итак, два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.

Следствие2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: P(AB)=P(A)P(B). Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С. Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Например, если события A₁, A₂, А₃, независимы в совокупности, то независимы события A₁ и А₂, А₁ и А₃, А₂ и A₃; А₁ и A₂A₃, A₂ и A₁A₃, А₃ и A₁A₂. Из сказанного следует, что если события независимы в совокупности, то условная вероятность появления любого события из них, вычисленная в предположении, что наступили какие-либо другие события из числа остальных, равна его безусловной вероятности. Подчеркнем, что если несколько событий независимы попарно, то отсюда еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости.

Пример:. Пусть в урне имеется 4 шара, окрашенные: один — в красный цвет (А), один — в синий цвет (В), один — в черный цвет (С) и один — во все эти три цвета (АВС). Чему равна вероятность того, что извлеченный из урны шар имеет красный цвет?

Так как из четырех шаров два имеют красный цвет, то Р(А) = 2 / 4 = 1 / 2. Рассуждая аналогично, найдем Р (В) = 1 / 2, Р (С) = 1/ 2. Допустим теперь, что взятый шар имеет синий цвет, т. е. событие В уже произошло. Изменится ли вероятность того, что извлеченный шар имеет красный цвет, т. е. изменится ли вероятность события А? Из двух шаров, имеющих синий цвет, один шар имеет и красный цвет, поэтому вероятность события А по-прежнему равна 1 / 2. Другими словами, условная вероятность события А, вычисленная в предположении, что наступило событие В, равна

41(2)

его безусловной вероятности. Следовательно, события А и В независимы. Аналогично придем к выводу, что события A и С, В и С независимы. Итак, события А, В и С попарно независимы.

Независимы ли эти события в совокупности? Оказывается, нет. Действительно, пусть извлеченный шар имеет два цвета, например синий и черный. Чему равна вероятность того, что этот шар имеет и красный цвет? Лишь один шар окрашен во все три цвета, поэтому взятый шар имеет и красный цвет. Таким образом, допустив, что события В и С произошли, приходим к выводу, что событие А обязательно наступит. Следовательно, это событие достоверное и вероятность его равна единице. Другими словами, условная вероятность Р_BC (A)= 1 события А не равна его безусловной вероятности Р (А) = 1 / 2. Итак, попарно независимые события А, В, С не являются независимыми в совокупности.

Приведем теперь следствие из теоремы умножения. Следствие: Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий: Р (А₁А₂ ... А_n) = Р (А₁) Р (А₂) ... Р (А_n). Предположим, что событие A может осуществиться с одним и только с одним из n несовместимых событий В₁,В₂…В_n. Т.е.: A = АВ₁ +АВ₂ +…+ АВ_n, где АВi,и АВj с разными индексами i и j несовместимы. По теореме сложения вероятностей имеем: P(A) = P(АВ₁ + АВ₂ +… +АВ_n) = P(АВ₁)+ P(АВ₂)+… +P(АВ_n ) По теореме умножения для каждого слагаемого имеем: P(AB_i)=P(B_i)P(A|B_i). Следовательно P(A) = P(B₁)P(A|B₁) +P(B₂)P(A|B₂)+…+P(B_n)P(A|B_n). Или P(A) = P(B_i)P(A|B_i) Эта формула называется формулой полной вероятности.

Пример:В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов?

Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а Н1, Н2, Н3 и Н4 — гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны

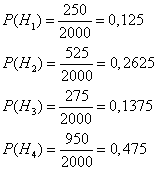
Далее, из условия задачи следует, что

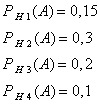
Используя формулу полной вероятности, имеем

ФОРМУЛА БАЙЕСА

П

41(3)

усть дана группа несовместных событий В₁, В₂ ,…В_n и некоторое событие А, подразделяющееся на частные случаи АВ₁, АВ₂,… АВ_n. И пусть даны вероятности P(В₁), P(В₂ ),…,P(В_n) и условные вероятности P(A|B₁), P(A|В₂ ),…,P(A|В_n). Требуется определить условные вероятности P(В₁|A), P(В₂|A),…,P(В_n|A).

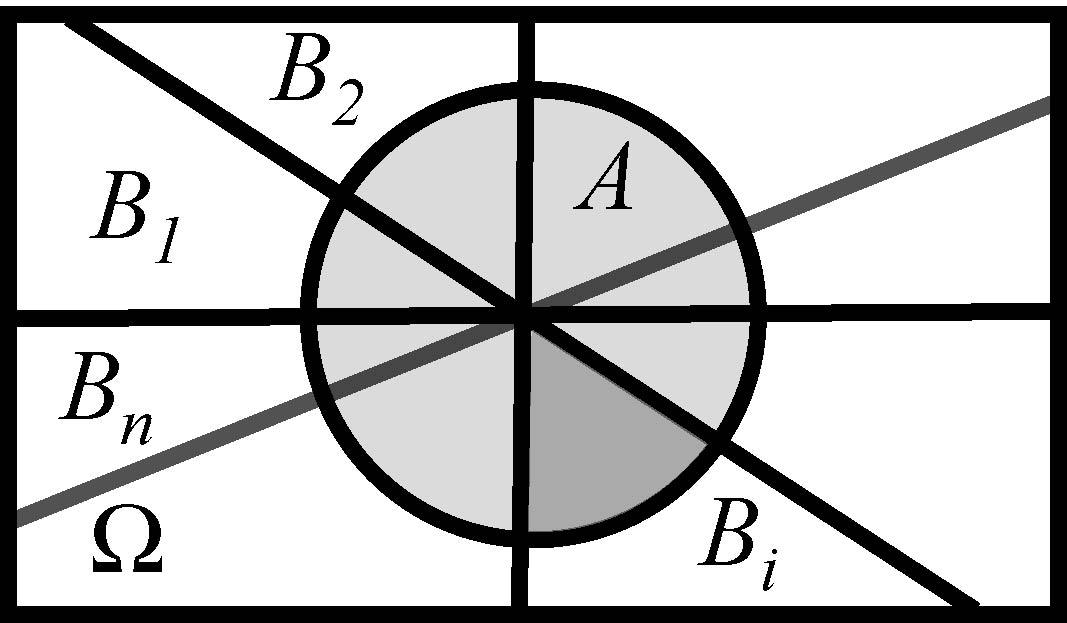
Рис 3. Пояснение к формуле Байеса

По теореме умножения P(AB) = P(B)P(A|B) или P(AB) = P(A)P(B|A). Следовательно, P(B)P(A|B)=P(A)P(B|A). Воспользуемся последним равенством и выразим P(B|A) в общем случае .

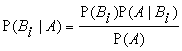P(A) находим по формуле полной вероятности P(A) = P(B_i ) P(A | B_i )). Итак,

.

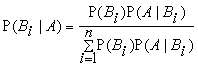Эта формула называется формулой Байеса.

Вероятность Р(В_i) осуществления события В_i (i = 1,…,n), вычисления безотносительно к событию А, называется априорной вероятностью (a priori). Условная вероятность Р(В_iА) выполнения события В_i (i = 1,…,n), вычисленная в предположении, что событие А осуществилось, называется апостериорной вероятностью (a posteriori).

События В_i называют гипотезами, а теорему Байеса теоремой гипотез.

Формулы полной вероятности и Байеса связаны между собой и дают прямое и обратное решения одной и той же проблемы. Первая прогнозирует возможность появления события А по известным до опыта вероятностям осуществления гипотез. Последняя оценивает вероятность осуществления каждой гипотезы, если событие А произошло.

Пример:

Студенту предложили решить числовую задачу. Ответ задачи известен и представляет собой одно из чисел 1, 2, 3, 4, 5. Решая задачу, студент может либо найти правильный путь решения задачи, либо ошибиться. Подготовка студента такова, что он находит правильный путь решения задачи с вероятностью 0.6. В этом случае ответ, полученный им, совпадает с данным.

С дополнительной вероятностью 0.4 студент ошибается. В этом случае мы будем предполагать, что в качестве ответа может получиться любое из чисел 1,2,3,4,5 с равной вероятностью, равной (1/5)=0.2. Известно, что студент получил правильный ответ.

Какова при этом условии вероятность того, что он верно решил задачу?

Решение: Определим случайные события: А-студент получил правильный ответ; H1-студент решил задачу верно; H2-студент решил задачу неверно; Действительно, студент не может одновременно решить задачу правильно и неправильно, значит,Н1 и Н2 независимы. И, если он получил правильный ответ, то он либо решил задачу верно, либо нет(то есть "угадал"). Тогда по условию P(H1)=0.6; P(H2)=0.4.Очевидно, что Р(А|Н1)=1; Р(А|Н2)=0.2 (следует из условия).Таким образом по формуле Байеса получаем:

P

41(4)

(H1)*P(A|H1)

P(H1|A)=---------------------------------=

P(H1)*P(A|H1) + P(H2)*P(A|H2)

0.6*1

=---------------~0.88

0.6*1+0.4*0.2

Если студент получил правильный ответ, то вероятность того, что он верно решил задачу, примерно равна 0.88

Пример. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался н естандартным. Какова вероятность того, что он изготовлен 1-м заводом?

Решение: Пусть A — событие, состоящее в том, что взятый Подшипник нестандартный, а - гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют

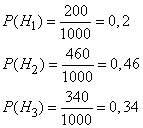
Из условия задачи следует, что

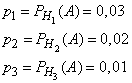
Найдем , т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем

Таким образом, вероятность гипотезы, что подшипник изготовлен 1-м заводом, изменилась после того, как стало известно, что он нестандартен.

А

41(5)

лгоритм линейного поиска в одномерном массиве. Зависимость затрат на линейный поиск в среднем и в худшем случае от числа элементов массива. Улучшение линейного поиска: поиск с барьером.

Одномерный массив представляет собой последовательность однородных элементов, доступ к которым осуществляется по индексу в массиве. Как правило, в реализации массива элементы хранятся последовательно в сплошном блоке памяти.Самым простым алгоритмом поиска значения в одномерном массиве является алгоритм линейного (или последовательного) поиска. Каждый элемент массива последовательно сравнивается с искомым значением. Если требуемое значение найдено, возвращается его индекс в массиве. Если значение не найдено и достигнут последний элемент массива, то поиск завершился неудачей.

Запишем алгоритм на псевдокоде:

Пусть имеется массив из N элементов (N≥1) K_i. Ищем элемент, равный заданному значению K. Используем переменную i.

S1 [Начальная установка] установить i = 1

S2 [Сравнение]

ЕСЛИ K=K_i, ТО алгоритм окончился удачно(элемент найден).

S3 [продвижение] увеличить i на 1.

S4 [Конец массива?]

ЕСЛИ i≤N, ТО перейти к шагу S2.

ИНАЧЕ алгоритм закончился неудачно (элемент не найден).

Ясно, что в худшем случае для несортированного массива (если искомый элемент отсутствует в массиве и находится в самом его конце) поиск потребует N сравнений. В среднем потребуется осуществить (N+1)/2 сравнений.

Сложность алгоритма O(N).

Покажем расчет количества сравнений в среднем:

Вероятности нахождения искомого элемента на любой позиции в массиве одинаковы.

Позиция	1	2	3	...	N
Число сравнений	1	2	3	...	N

Тогда в среднем придется сделать :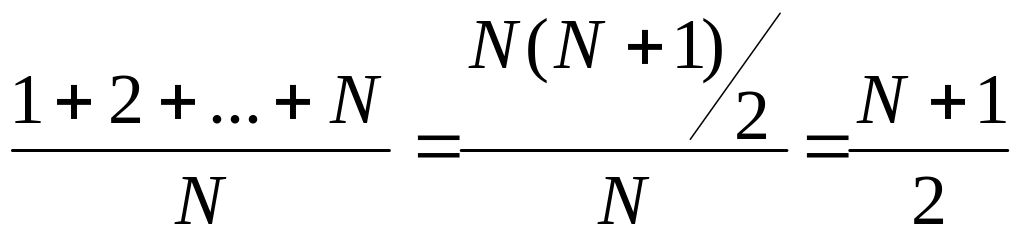

Для упрощения записи условия выхода из цикла используют алгоритм поиска с барьером. Массив увеличивают на один элемент и записывают последним элементом искомое значение. При этом алгоритм всегда будет успешен (искомое значение заведомо присутствует в массиве) а определить результат поиска можно только по полученному индексу. Если значение найдено в ячейке N+1, то поиск закончился неудачей.

Запишем алгоритм на псевдокоде:

Предположим, что поиск осуществляется в условиях алгоритма линейного поиска. Однако, в конец массива добавляется элемент N+1 со значением K.

S1 [начальная установка] установить i=1 и K_N+1=K

S2 [сравнение] ЕСЛИ K=K_i, ТО перейти к S4

S3 [продвижение]увеличить i на 1 и вернуться к шагу S2

S4 [конец файла?]

ЕСЛИ i≤N, ТО алгоритм закончился удачно (элемент найден);

ИНАЧЕ алгоритм закончился неудачно (элемент не найден).

Преимуществом поиска с барьером является то, что сравнение величин i и N вынесено из цикла и выполняется однократно. Таким образом, чем больше величина N, тем больше выигрыш.

Н

41(6)

ормальные формы отношений. 1НФ, 2НФ, 3НФ, БКНФ.

Первая и вторая нормальная форма.