Теорема гипотез (формула Байеса)

Пусть имеется полная группа попарно несовместных событий . Причём заранее (априорно) известны вероятности . Событие может сопутствовать любой из гипотез с вероятностями:

, .

Произведём эксперимент, в результате которого имело место событие . Возникает вопрос, с какой вероятностью произошло событие с одной из гипотез? Иначе говоря, как следует изменить априорные вероятности гипотез? Т.е. чему равна вероятность:

? Оказывается:

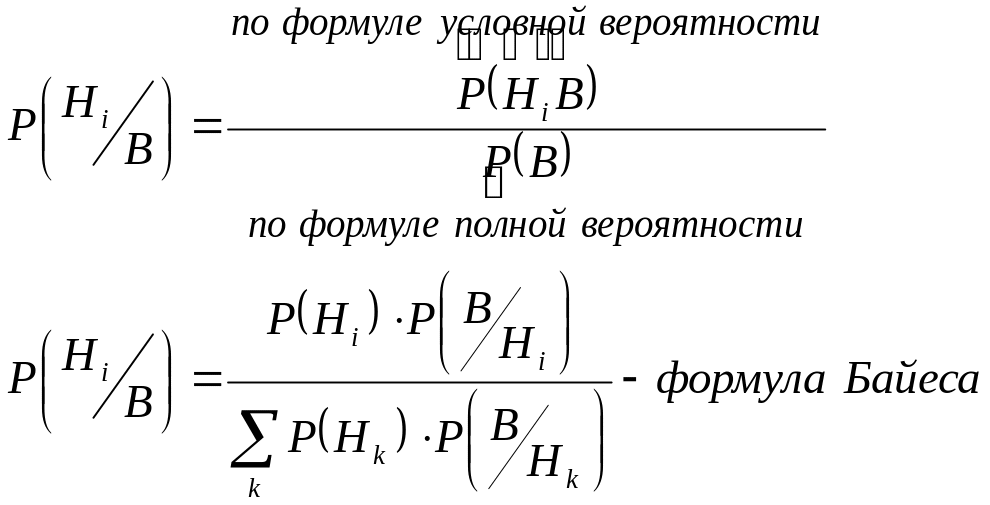
Пример: Два стрелка независимо стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для 1-ого стрелка: 0,8, для второго: 0,4. После стрельбы в мишени обнаружена 1 пробоина. Найти вероятность того, что она принадлежит 1-ому стрелку. До опыта возможны следующие гипотезы:

• H₁ – никто не попадет, P(H₁) = (1-0,8)(1-0,4)=0,12

• H₂ – оба попадут, P(H₂) = 0,8*0,4=0,32

• Н₃ – только 1-ый попадет, P(H₃) = 0,8(1-0,4)=0,48

• Н₄ – только 2-ой попадет, P(H₄) = (1-0,8)0,4=0,08

Условные вероятности наблюденного события А при этих гипотезах:

P(А│H₁)=0; P(А│H₂)=0; P(А│H₃)=1; P(А│H₄)=1

После опыта гипотезы H₁ и H₂ становятся невозможными, а вероятности гипотез H₃ и H₄ будут равны:

;

2 19(4) . Логическое высказывание и его свойства. Логические операции (связки). Формализация логических суждений.

Основным понятием математической логики является «простое высказывание».

Простое высказывание – это некоторое повествовательное предложение, которое может быть либо истинно, либо ложно, но не то и другое одновременно. Простое высказывание обозначается маленькими латинскими буквами.

Высказывания, которые получаются из простых с помощью грамматических связок «и», «или», «не», «тогда и только тогда», «либо…либо…», «если …то…» называются составными или формулами алгебры логики. Ф-лы алгебры логики обозначаются большими латин. буквами.

Формула А, всегда истинная, называется тождественно истинной формулой или тавтологией, А=1.

Формула В, всегда ложная, называется тождественно ложной формулой В=0.

Рассматривая высказывания, мы абстрагируемся от их смысла, нас интересует их истинность или ложность. Мы пишем а=1, если а- истинно, и а=0, если а- ложно.

Рассмотрим основные операции над высказываниями.

Дизъюнкция V	Конъюнкция &	Отрицание `a
Импликация ®	Эквивалентность ~	Жегалкинское сложение Å

Операции логическое сложение, логическое умножение, отрицание, импликация и эквивалентность составляют сигнатуру алгебры логики[1].

Значение каждой логической операции описывается таблицей истинности.

Таблица истинности представляет собой таблицу, устанавливающую соответствие между возможными значениями наборов переменных и значениями операции [2].

Дизънкция a V b. Читается эта запись или “а дизъюнкция б”. Дизъюнкция двух слагаемых ложна тогда и только тогда, когда ложны оба слагаемых. Соответствует союзу «ИЛИ». Таблица истинности у дизъюнкции: a b a + b 0 0 0 0 1 1 1 0 1 1 1 1	Конъюнкция a&b. Запись читается, “а конъюнкция б”. Конъюнкция двух сомножителей истинна тогда и только тогда, когда истинны оба сомножителя. Соответствует союзу «И». Таблица истинности конъюнкции: a b a ×b 0 0 0 0 1 0 1 0 0 1 1 1
Отрицание ` a. Запись читается, “не а”. Отрицание лжи есть истина, отрицание истины есть ложь. Соответствует частице «НЕ». Таблица истинности у отрицания следующая: a ` a 0 1 1 0	Импликация a® b Запись a®b читается, как “а импликация б” или “из а следует б. Для функции импликации из лжи следует все, что угодно, а из истины только истина. Таблица истинности импликации: a b a ®b Соответствует «если а, то в», «а является достаточным условием для в» 0 0 1 0 1 1 1 0 0 1 1 1 Запись a ¬ b соответствует «если в, то а», «а является необходимым условием для в»

19(5)

Жегалкинское сложение a Å b. Запись читается, как “а жегалкинское сложение б”. Операция жегалкинское сложение истинна тогда и только тогда, когда значения переменных различны. Таблица истинности: a b a Å b Соответствует «либо а, либо в», «или а, или в» 0 0 0 0 1 1 1 0 1 1 1 0

Эквивалентность a~b. Запись читается, как “а эквивалентно б”. Операция истинна тогда и только тогда, когда значения переменных совпадают. a b a ~ b Соответствует «тогда и только тогда, когда». 0 0 1 0 1 0 1 0 0 1 1 1

При работе с высказываниями мы отвлекаемся от их смыла, нас интересует только их истинность или ложность. Каждое высказывание – это повествовательное утверждение естественного языка. Несмотря на то, что естественный язык гораздо богаче высказываний алгебры логики, в следующей таблице приведем один из способов формализации сложных высказываний, т.е. построения формул алгебры логики.

Рассмотрим способы построения формул, при условии что а-« сегодня ясная погода», в – «сегодня идет дождь», с- «сегодня ветрено»

Союзы и частицы естественного языка	Операции алгебры логики	Примеры
а и в	a&b	Сегодня ветрено и идет дождь
а или в	a V b	Сегодня ясная погода, или сегодня идет дождь
а либо в	a V b	Сегодня ветрено, либо идет дождь
не а		Неверно, что сегодня идет дождь Сегодня пасмурно Сегодня безветренно Сегодня нет дождя
а достаточное условие для в	a ® b	Сегодняшний ветер - достаточное условие для сегодняшнего дождя
если а, то в	a ® b	Если сегодня ветер, то сегодня пойдет дождя
а необходимое условие в	b ® a	Сегодняшний ветер - необходимое условие для сегодняшнего дождя
а тогда и только тогда, когда в	a~b	Сегодня ветрено тогда и только тогда, когда идет дождь
либо а, либо в	a Å b	Либо сегодня идет дождь, либо ясная погода
или а, или в	a Å b	Или сегодня ветрено, или дождливо

Пример сложного высказывания: простые высказывания a = “Иван умён”, b = “Петр глуп”, c = “Иван выиграет состязание”.

“Если Иван умён и Петр глуп, то Иван выиграет состязание” =

“Иван выиграет состязание только в том случае, если он умён или(и) если Петр глуп” =

= “Если Петр глуп, а Иван не выиграет состязание, то Иван не умён” =