5. Уравнение парной линейной регрессии в отклонениях

Обозначим через — отклонения от средних по выборке. Задача: подабрать лин. ф-цию f(x)=a+bx минимизирующую функционал .

Из геометрич. соображений ясно, что решением будет та же прямая на плоскости (x,y), что и для исходных данных , только начало координат переместится в точку в т.( , ). Проделаем вычисления аналогичные тем, которые использовались для получения в методе МНК формул:

и , заменив на и учитывая, что :

Т.е. запишем необходимые условия экстремума:

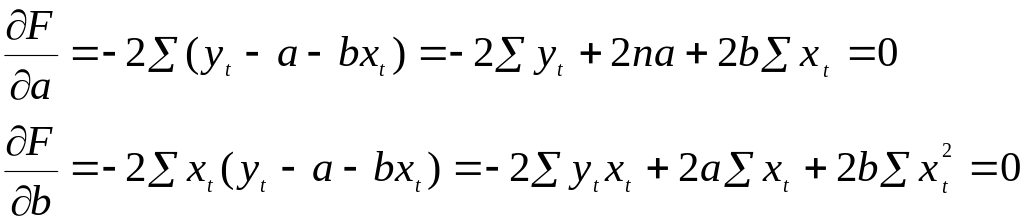
Поделив каждое уравнение на (-2), преобразуем и получим:

=>  т.к. .

6. Геометрическая интерпретация мнк. Матричная форма записи мнк.

Рассм. п-мерное векторное прост-во Rⁿ, в кот. определено стандартное евклидово скалярное произв-ние:

Где —транспонированная матрица-столбец (т.е. матрица строка).

Будем искать реш. в виде: , где a,b — числовые коэффициенты, — вектор, лежащий в двумерной гиперплоскости π, натянутой на векторы x и i. Предполагается, что векторы x и i — неколлинеарны.

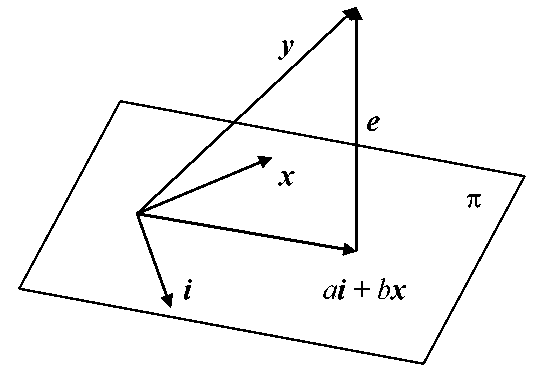Построим пл-ть π на векторах x и i, вектор ŷ может лежать только в этой пл-ти. Задача: чтобы ŷ наилучшим образом отображ. у. Задача сводится к мин-ции длины вектора е. Найти такие а и b, чтобы вектор е имел мин. длину.

Очевидно, что решением является такой вектор ŷ, для которого вектор е _┴ плоскости π. Необходимо и достаточно , чтобы е был ортогонален векторам i и х.) Т.е. (1)

Матричная форма записи:

Обозначим через Х матрицу размерности

.

Из того что нам известно е=у-Хβ, условие ортогональности (1) теперь записывается как Х'е = 0 или Х'(у-Хβ)=X'y-Х'Хβ=0, откуда получаем Х'Хβ=Х'у, а значит =(X'X)^-1X'y.

Если i и х линейно независимы, то матрица Х'Х обратима.

Зам: Матрица Х'Х невырождена, т.к. матрица X имеет максимальный ранг=2.

7. Линейный коэффициент корреляции. Коэффициент детерминации и его связь с коэффициентом корриляции.

Ур-ние регрессии дополняют показателем тесноты связи, для чего используют лин. коэф-т корриляции r_xy: 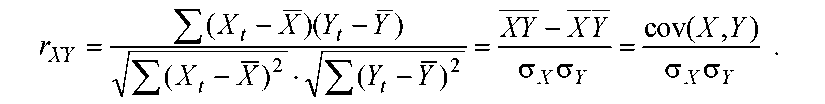(1)

С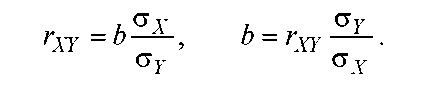 равнивая между собой выражения и (1) очевидна взаимосвязь м-ду коэффициентом регрессии b и линейным коэффициентом корреляции r_xy [-1;1]

(2)

З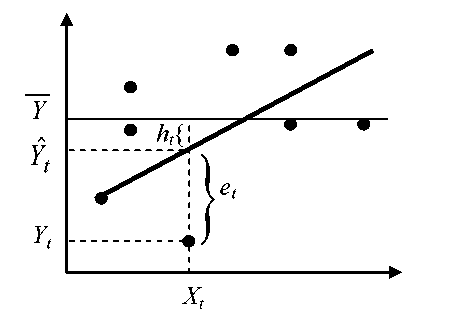 ам: Величина лин. коэф-та корреляции оценивает тесноту связи рассм-ых признаков в ее лин. форме. Поэтому близость его к 0 не означает отсутствие связи м-ду признаками,возможна связь даже очень тесная,но не линейная.

Введем понятие коэффициента детерминации, как долю дисперсии результативного признака У, объясняемую регрессией, в общей дисперсии результативного признака.

Пусть по реальным данным мн-во точек (X_t,Y_t), t=1,n построено эмпирическое ур-ние регрессии Ŷ=a+bX.

Тогда наблюдаемые значения Y_t можно записать в виде: Y_t=Ŷ_t+e_t (3), где Ŷ_t — теоретическое значения результатов регрессии. Равенство (3) не изменится, если из каждой части вычесть одну и туже величину Y_t- =(Ŷ_t- ) + e_t или Y_t- =h_t+e_t (4),

где Y_t- — отклонение t-ой наблюдаемой точки от среднего значения результирующей переменной;

h_t — отклонение t-ой точки на линии регрессии от ; e_t — отклонение t-ой точки от модельного значения Ŷ_t, определяемого по линии регрессии.

Возведем обе части (4) в квадрат и просуммируем результат по всем t

Можно показать, что Σ((Ŷ_t -Y)e_t)= 0. Тогда справедливо

(5)

Т.е. полная сумма квадратов м. интерпретироваться как мера общего разброса отклонения относительно . Σh_t² — объясненная сумма квадратов. Σe² — остаточная (необъясненная) сумма квадратов.

Разделив (5) на левую часть, получим:

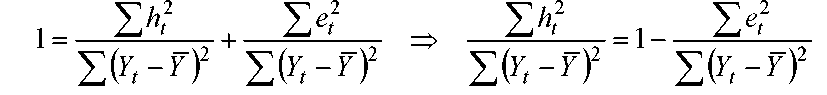
Умножим числитель и знаменатель на 1/n, получим коэф-т детерминации:

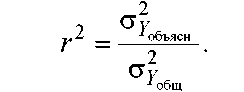
1–r² характеризует долю дисперсии Y, вызванную влиянием остальных, не учтенных в модели факторов.

Для качественной оценки линейной регрессии были введены линейным коэффициентом корреляции r_xy, кот. описывает степень плотности экспериментальных точек вокруг линии регрессии

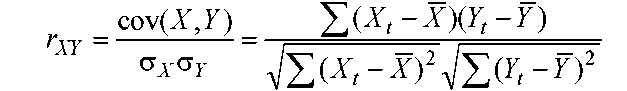
и линейный коэффициент детерминации r²

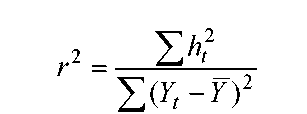
Найдем взаимосвязь между этими параметрами.