2. Линейность и аддитивность связей в функции

Ф-ция y = f (x₁,…,x_k) линейна по x_i  ∂y/∂x_i не включает x_i, т.е. ∂(∂y/∂x_i)=0. Это значит, что эффект от изменения по x_i не зависит от x_i.

Ф-ция y=f(x₁,…,x_k) явл. аддитивной по всем независимым переменным  для любого i dy/dx_i не включает x_j (j ≠ i) т.е. ∂(∂y/∂x_i)/∂x_j=0. Это значит, что эффект от изменения по каждой независимой переменной не зависит от уровня др. переменной. В этом случае совместный эффект изм-ния по всем учтенным независимым переменным может быть получен сложением отдельно вычисленных эффектов изменений по каждой из них.

Примеры оценки линейности и аддитивности функций

Ф-ция f (x1, x2)	∂f/∂x1	∂f/∂x2	Лин-ть		Аддит-ть по x1,x2
			x1	x2
a1x21+a2x22+a3x1x2	2a1x1+а3x2	2a2x2+a3x1	нет	нет	нет
a1x21+a2x22	2a1x1	2a2x2	нет	нет	да
x2/x1	-x2/x12	1/x1	нет	да	нет
a1x21+a2x2	2a1x1	a2	нет	да	да
a1x1x22+a2logx2	a1x22	2a1x1x2+a2/x2	да	нет	нет
a1x1+a2x2+a3x1x2	a1+a3x2	a2+a3x1	да	да	нет

3. Типы данных. Выбор вида функции парной регрессии.

При моделировании экономических процессов встречаются 3 типа данных:

Пространственные данные – данные снятые в один момент или отрезок времени, или время не имеет знач. для этих данных (объем произв-ва, кол-во работников и т.д.).

Временные данные – отслеживание за одним показателем (осн. показ-ль– время).Прим.: ежеквартальные данные по инфляции, средней зарплате и т.д.

Панельные данные– замеры произв-ся по времени, но для одной и той же совок-ти (ежегодные обследования одних и тех же предприятий или домашних хозяйств).Т.о. панельные данные объединяют в себе как пространственные данные так и временные ряды.

Корреляционное поле – отображение парной взаимосвязи, для каких-то эконом. параметров.

Простая или парная регрессия представляет собой регрессию между 2-мя переем-ми — у и х. Т.е. модель вида: y=f(x), у — завис-ая перем-ная(результативный признак), а х — независимая, или объясняющая, переменная (признак-фактор или регрессор).

На практике величина у складывается из двух слагаемых:y= y ˆ_{x+ ,}где СВ , характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. СВ наз. ошибкой или возмущением.

В парной регрессии выбор вида ф-ции у_х=f(x) осущ-ся 3-мя методами: графическим (строится корреляционное поле и по его виду делается предположение о форме линии корреляции), аналит-им (т.е. исходя из теории изучаемой взаимосвязи) и экспериментальным.

4. Смысл и оценка параметров линейной регрессии. Мнк.

Пусть имеется набор двух переменных X_t и Y_t ,t=1,…,n;можно отобразить пары (X_t,Y_t)точками на плоскостиXY. Пусть нашей задачей явл. подобрать ф-цию Y=f(X, ), где —неизвестные парам., наилучшим образом описывающую зависимость Y от X. Подобрать ф-цию означает выбрать наилучшее знач. парам. .Простейшим примером служит семейство линейных функций:

В качестве меры отклонения ф-ции f(X, ) от набора наблюдений м. взять след. функционалы, кот. необходимо минимизировать:

1. Сумму квадратов отклонений

2. Сумму модулей отклонений .

3. Д ля того чтобы устранить те или иные недостатки исп-ся: 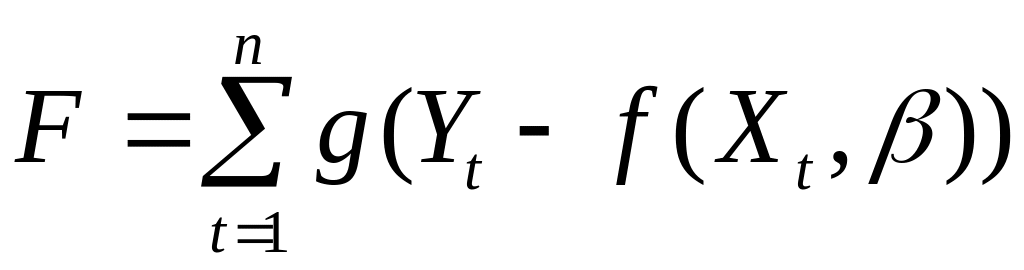, где g — «мера», с которой отклонение входит в функционал F.

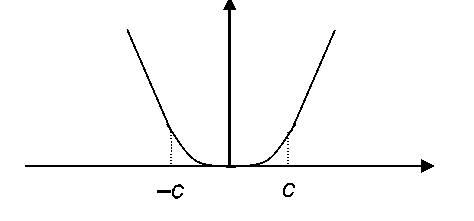
Функция Хубера:

МНК: рассм. задачу «наилучшей» аппроксимации набора наблюдений Х_t, Y_t, t=1,...,n –линейной ф-ции f(X)=а+bX в смысле минимизации функционала (1) , a,b – неизвестные, для их оценки необх:

Запишем необходимые условия экстремума:

Поделив каждое уравнение на (-2), преобразуем в стандартную форму нормальных уравнений и получим: (2)

=> и

Поделив числитель и знаминатель на n², получим: (3а) (cov – ковариация, var – дисперсия) (3б).

Параметр b наз. коэффициентом регрессии, он показывает среднее изменение результата при изменении регрессора на одну единицу. Формально а — значение у при х = 0. Если же фактор х по своей природе не м. иметь нулевого значения, то такая трактовка не им. смысла.