2.3.1 Расчет погрешности ацп

На выходе АЦП каждому дискретному значению соответствует комбинация двоичного кода, число разрядов которого (включая нулевое) обозначим буквой Np. Выбор Np производится в соответствии с соотношением:

.(2.2)

Число дискретных значений Nд (уровень квантования) зависит от погрешности квантования по уровню.

Абсолютная погрешность, появляющаяся при квантовании по уровню:

,(2.3)

где ∆U величина шага квантования по уровню, равная

.(2.4)

Из приведенного соотношения следует, что максимальная абсолютная погрешность равна половине шага квантования по уровню. Относительная погрешность квантования по уровню:

,(2.5)

где Nд – число дискретных значений выходной величины (уровней квантования). В формуле (2.5) из Nд вычитается единица, т.к. одним из дискретных значений (уровней) является нулевое (рисунок 2.3). Отсюда требуемое число уровней дискретных значений, которое отражает нашу непрерывную функцию с заданной точностью, определяется из выражения:

(2.6)

Пример расчета АЦП

Задано значение относительной погрешности дотн £ 2%.

Требуется определить разрядность АЦП, удовлетворяющего заданному значению дотн.

Определяем число уровней квантования (число дискретных значений):

Ny 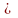(50/2)+1=26.

Выбираем число разрядов АЦП Np ДК=5, что удовлетворяет выражению (2.5):

25=32>26.

2.3.2 Выбор величины шага квантования по времени

Величина шага квантования по времени ∆t, определяющая требуемое быстродействие АЦП, рассчитывается в соответствии с теоремой взятия отсчетов (теоремой Котельникова)

,(2.7)

где Fmax – частота высшей гармоники частотного спектра входного аналогового сигнала. Иными словами при переходе к дискретной величине для гармонической составляющей входного сигнала, имеющей минимальный период (максимальную частоту), необходимо взять не менее двух отсчетов.

Любой АЦП является инерционным устройством, имеющим конечное время преобразования tпрб, которое должно удовлетворять требуемому значению ∆t.

Если входной аналоговый сигнал меняется достаточно быстро, а АЦП имеет низкое быстродействие, то может появиться апертурная погрешность, выражающаяся в том, что за время преобразования АЦП изменение входного сигнала эквивалентно изменению выходного ДК больше, чем на единицу МЗР. Для борьбы с этим явлением применяют устройства выборки-хранения (УВХ), которые запоминают мгновенное значение входного аналогового сигнала в момент временной выборки и поддерживают это значение постоянным до следующей выборки.

При проектировании компьютеризированных систем часто возникает обратная задача: преобразование цифрового сигнала в аналоговый (непрерывный). Для этого применяют цифро-аналоговые преобразователи (ЦАП).

3. Применение алгебры логики (булевой алгебры) при анализе и синтезе цифровых электронных устройств

3.1 Определение и способы задания переключательных функций

В цифровой электронике существуют логические задачи, особенностью которых является то, что их условия и решения могут принимать одно из двух возможных значений. Одно выражает наступление того или иного события, а другое – не наступление его. Наступление события обозначают единицей (логической единицей), а ненаступление - нулем (логическим нулем). Устройства, предназначенные для решения логических задач, называют логическими электронными устройствами (ЛЭУ).

Математическим аппаратом, применяемым при анализе и синтезе ЛЭУ, является алгебра логики, разработанная в середине Х1Х века английским математиком Дж. Булем, и поэтому часто называемая Булевой алгеброй (БА).

БА оперирует с двоичными (логическими) переменными, принимающими одно из двух значений: логический нуль или логическая единица.

Функция двоичных переменных также равная одному из двух значений (нулю или единице) - называется переключательной (логической) функцией (ПФ).

Логические функции обозначаются прописными буквами F или Y, а двоичные переменные - А, В, С, D, E, ... или строчной буквой икс с индексом, например, x1, х2, х3 ... .

ПФ может быть выражена (задана):

• словесно;

• алгебраическим (булевым) выражением;

• таблицей истинности;

• диаграммой Вейча (картой Карно).

Примеры задания переключательной функции (ПФ):

1) словесно: функция двух переменных принимает значение логической единицы, если обе переменные также равны единице, в противном случае, она равна нулю;

2) выражением:

3) таблицей истинности (таблица 3.1)

Таблица включает наборы (комбинации) логических переменных, которые должны быть упорядочены по возрастанию или убыванию их десятичных эквивалентов, а также значения функции на каждом наборе. Каждый набор имеет номер, равный десятичному эквиваленту двоичного числа, если наборы упорядочены по возрастанию. Если число переменных равно n, то количество наборов N = 2n. Номера наборов изменяются от 0 до (2n-1). Общее число переключательных функций n – переменных

.(3.1)

Таблица 3.1

№ набора	В	А	F
0	0	0	0
1	0	1	0
2	1	0	0
3	1	1	1

Представление переключательной функции диаграммой Вейча (картой Карно) будет рассмотрено позднее при изучении вопроса минимизации ПФ.

3.2 Переключательные функции одной переменной (n=1)

Если n=1, то число наборов N=21=2, а количество ПФ (таблица 3.2)

Таблица 3.2

N набора	A	F0	F1	F2	F3
0	0	0	1	0	1
1	1	0	0	1	1

Функция F0 называется константой нуля, так как на всех наборах принимает нулевое значение (F0=0). Функция F3 - константа единицы, так как всегда равна единице (F3=1). Функция F2=A называется повторением, а – инверсией (отрицанием – не А).

3.3 Переключательные функции двух переменных (n=2)

Если n=2, то число наборов N=22 =4, а количество ПФ (таблица 3.3)

Отметим из этих шестнадцати функций 2-х переменных наиболее часто использующиеся:

F0 – константа нуля;

F15 – константа единицы;

F8=А В=А*В – конъюнкция (логическое умножение (логическое “И”));

F14=А В=А+В – дизъюнкция (логическое сложение (логическое “ИЛИ”));

F6= – исключающее ИЛИ (сумма по модулю два, неравнозначность, неэквивалентность);

– равнозначность (эквивалентность);

– ИЛИ-НЕ;

– И - НЕ.

Таблица 3.3

№ набора	В	А	F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15
0	0	0	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
1	0	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
2	1	0	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
3	1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1