5.2 Реализация логических функций в различных базисах

5.2.1 Реализация элемента “Равнозначность” (исключающее или - не)

На выходе такого элемента должна быть логическая 1, если на входах одновременно присутствуют одинаковые логические переменные (единицы или нули).

Булево выражение логической функции, соответствующей рассматриваемому элементу имеет вид

.(5.1)

Очевидно, что данное выражение легко реализуется элементами базиса И, ИЛИ, НЕ.

Используя теорему де Моргана и тождества булевой алгебры, преобразуем выражение (5.1) к виду, позволяющему реализовать функцию “равнозначность” в базисе И-НЕ (5.2) и ИЛИ-НЕ (5.3)

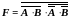,(5.2)

.(5.3)

Ниже показаны функциональные схемы элемента “равнозначность” на ЛЭ базисов И, ИЛИ, НЕ (рисунок 5.2,а); И-НЕ (рисунок 5.2,б) и ИЛИ-НЕ (рисунок 5.2,в).

А Б

В

Рисунок 5.2

5.2.2 Реализация элемента “Неравнозначность” (исключающее или, сумма по модулю два)

На выходе такого элемента должна быть логическая 1, если на входах присутствуют неравнозначные логические переменные:

F = 1, если А = 1, В = 0 или А = 0, В = 1.

Булево выражение логической функции рассматриваемого элемента имеет вид

.(5.4)

Это выражение может быть легко реализовано элементами базиса И, ИЛИ, НЕ. Применяя теорему де Моргана и тождества булевой алгебры, преобразуем выражение (5.4) к виду, позволяющему реализовать функцию “неравнозначность” в базисе И-НЕ (5.5) и ИЛИ-НЕ (5.6).

,(5.5)

.(5.6)

Ниже показаны функциональные схемы элемента “неравнозначность” на ЛЭ базисов И, ИЛИ, НЕ (рисунок 5.3, а); И-НЕ (рисунок 5.3, б) и ИЛИ-НЕ (рисунок 5.3, в).

А Б

В

Рисунок 5.3

Элемент “неравнозначность” иначе называют сумматором по модулю два: сумма двоичных цифр дает единицу, если одна из них единица, а другая – нуль; в противном случае, если обе цифры 0 или 1, то сумма равна нулю.

5.2.3 Реализация элемента “Запрет”

На выходе такого элемента должна быть логическая 1, если на основном входе присутствует логическая единица, а на запрещающем входе – логический нуль.

Булево выражение логической функции рассматриваемого элемента имеет вид

.(5.7)

Выражение (5.7) может быть легко реализовано в базисе И, ИЛИ, НЕ.

Применяя теорему де Моргана и тождества булевой алгебры, преобразуем выражение (5.7) к виду, позволяющему реализовать функцию “запрет” в базисе И-НЕ (5.8) и ИЛИ-НЕ (5.9).

,(5.8)

.(5.9)

Ниже показаны функциональные схемы элемента “запрет” на ЛЭ базисов И, ИЛИ, НЕ (рисунок 5.4, а); И-НЕ (рисунок 5.4, б) и ИЛИ-НЕ (рисунок 5.4, в).

Рисунок 5.4

5.2.4 Реализация многобуквенных логических функций на элементах с небольшим количеством входов

Иногда на практике возникает задача реализовать логическую функцию большого числа логических переменных (многобуквенную функцию) на элементах с небольшим количеством входов. В качестве примера на рисунке 5.5 показана функциональная схема, реализующая логическую функцию

(5.10)

на двухвходовых элементах И-НЕ.

Рисунок 5.5

6. Параметры и характеристики цифровых интегральных микросхем (имс)

Цифровая микросхема как функциональный узел характеризуется набором сигналов, которые можно разделить на информационные (Х1, Х2, ..., Хn – входные, Y1, Y1, ..., Ym – выходные) и управляющие (V1, V2, ..., Vk). Каждая конкретная ИМС в соответствии со своим функциональным назначением выполняет определенные операции над входными сигналами (переменными), а выходные сигналы представляют собой результат этих операций Yj = F(Х1,Х2, ... ,Хn). Операторами F могут быть как простейшие логические преобразования, например, И, ИЛИ, НЕ, и т. д., так и сложные многофункциональные преобразования, имеющие место, например, в микропроцессорах, БИС памяти и др.

Сигналы управления определяют вид операции, режим работы ИМС, обеспечивают синхронизацию, установку начального состояния, стробируют входные и выходные сигналы, задают адрес, и т. д.

От функциональной сложности ИМС зависит и система ее электрических параметров, которые в общем случае могут иметь десятки наименований, причем многие из параметров характерны только для ИМС какого-либо одного класса. Поэтому ниже рассмотрим те параметры и характеристики, которые характеризуют большинство микросхем. В дальнейшем при изучении отдельных устройств этот перечень по мере необходимости будет расширен.