Тень в разрезе по­мещения цилиндрической формы с круглым отверстием (рис. 242).

Тени могут быть построены без второй проекции. План приведен для пояснений.

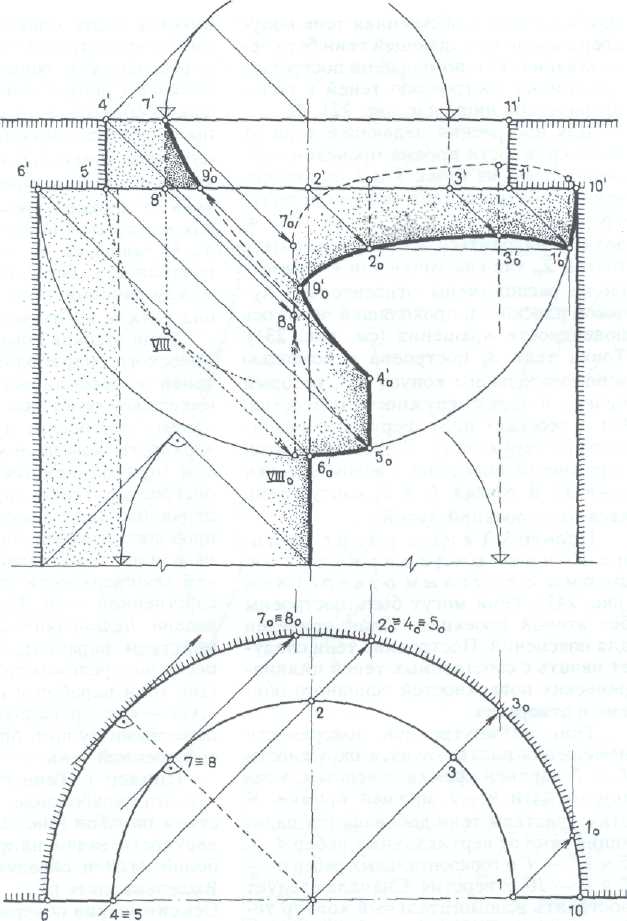
Построение тени следу­ет начать с собственных теней цилинд­рических поверхностей основного объ­ема и отверстия.

Тень на внутренней поверхности помещения падает от дуги окружности 4' — 7’ верхней кромки отверстия, а за­тем от дуги 9_О—1' нижней кромки.

К этим участкам тени добавляются пада­ющие тени от вертикальных ребер 4' — 5' и 11’ — 1’ и горизонтальных ребер 6' — 5' и 1’ — 10' отверстия.

Сначала следует построить вспомогательный контур те­ни — полуокружность 6' — 10’, как от кромки перекрытой ниши (см. рис. 220, б) и выделить в нем два участка 10’ — 1’_о и 5'₀ — 6'₀.

Построение точек те­ни 2’o, 3'₀ и 4'₀ понятно из чертежа.

Для того чтобы закончить построение тени от нижней кромки отверстия, необходи­мо построить вспомогательную (мни­мую) тень от теневой образующей 7’ — 8' отверстия.

Ее можно построить, совместив часть плана (пунктирные ли­нии) и проведя луч через точку VIII до пересечения с совмещенным планом большого полуцилиндра в точке VIII_o.

Таким образом, тень от нижней кромки пройдет через точки 1’o,3'o: 2'₀ через мни­мую тень точки 8₀ (где коснется верти­кали) и далее к точке 5'₀.

Падающую тень от верхней кромки 4' — 7’ строят как в открытой нише (см. рис. 220, а).

Оставшаяся ее часть перейдет на поверхность большого полуцилиндра между точками тени 9'₀ и 4'₀.

В точке 4'₀ она должна коснуться проекции луча.

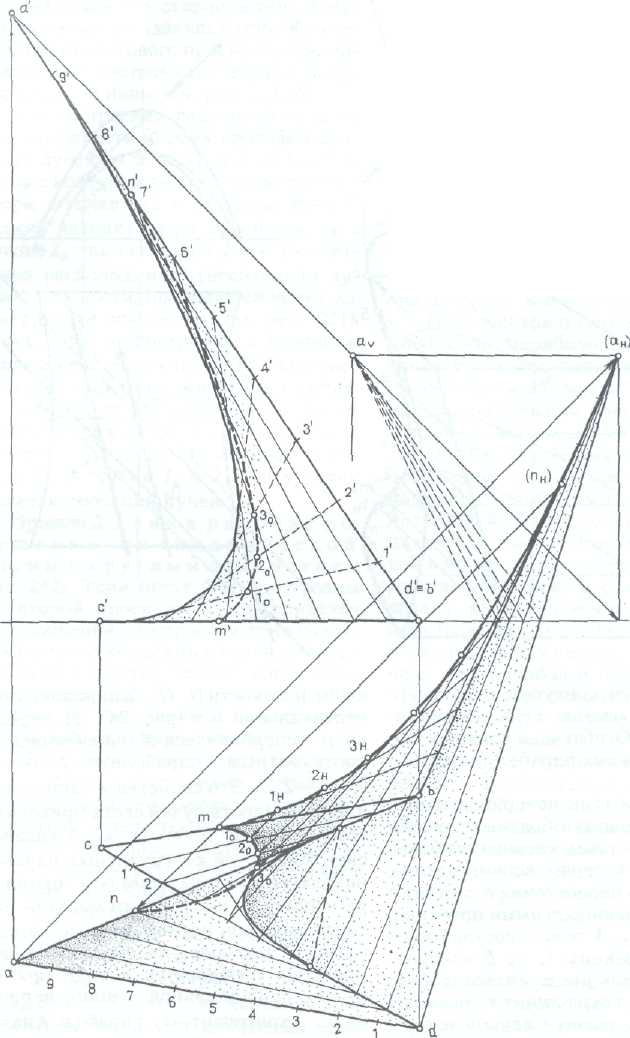
Тени отсеков поверхности гипербо­лического параболоида. Построение теней гиперболического параболоида имеет свои особенности. Возможны два приема построения теней: 1) если по­верхность задана линейчатым карка­сом (прямолинейными образующими), построение теней упрощается; строят падающие тени прямых образующих и проводят огибающую кривую контура падающей тени; способом обратных лу­чей на поверхности определяют контур собственной тени; 2) если поверхность задана нелинейчатым каркасом (се­мейством парабол), построение теней несколько усложняется. Строят падаю­щие тени парабол и проводят огибаю­щую — контур падающей тени, затем обратными лучами определяют контур собственной тени.

Пример 1. Тени отсека гиперболи­ческого параболоида, заданного семей­ством парабол (рис. 243, а)¹. Отсек по­верхности задан направляющей пара­болой АОВ и образующей параболой. Выделены пять (/, ..., V) ее положений. Ось симметрии поверхности вертикаль­на. Направляющие плоскости фрон­тальные.

Для построения контура падающей тени необходимо построить падающие тени всех пяти парабол по пяти точкам (см. тень пятой параболы), а затем про­вести огибающую кривую 1_Н, ..., 5_К, ко-

торая и является контуром падающей тени вместе с частью тени первой и пятой парабол. Огибающая кривая и те­ни вспомогательных парабол также па­раболы.

Собственная тень поверхности по­строена с помощью обратных лучей, проведенных из точек касания огибаю­щей параболы к теням вспомогатель­ных парабол до пересечения с соответ­ствующими горизонтальными проекци­ями парабол /, ..., V поверхности. Гори­зонтальная проекция Д ..., J контура собственной тени представляет собой прямую линию, а сама линия тени явля­ется параболой, расположенной в вер­тикальной плоскости, ее фронтальная проекция ~ парабола 1', ..., 5. Эта осо­бенность объясняется следующим обра­зом. Лучевые горизонтально проецирующие плоскости (/, //,...), параллельные вертикальной оси (рис. 243, 6), пересе­кают гиперболический параболоид по конгруэнтным параболам /—о,—1; 2~о₂—2,...). Это свойство и одинаковая направленность лучей света приводят к тому, что все точки (kj к,—) касания световых лучей конгруэнтных парабол находятся на одинаковом расстоянии от их вершин (0,0^...). Таким образом, все точки касания, расположенные на оги­бающей параболе, на горизонтальной проекции изобразятся в виде прямой к,—к2, параллельной линии вершин (о_х o_v..) конгруэнтных парабол. Анало­гичный пример был приведен на рис. 230.

Следовательно, если у гиперболиче­ского параболоида направляющие пло-

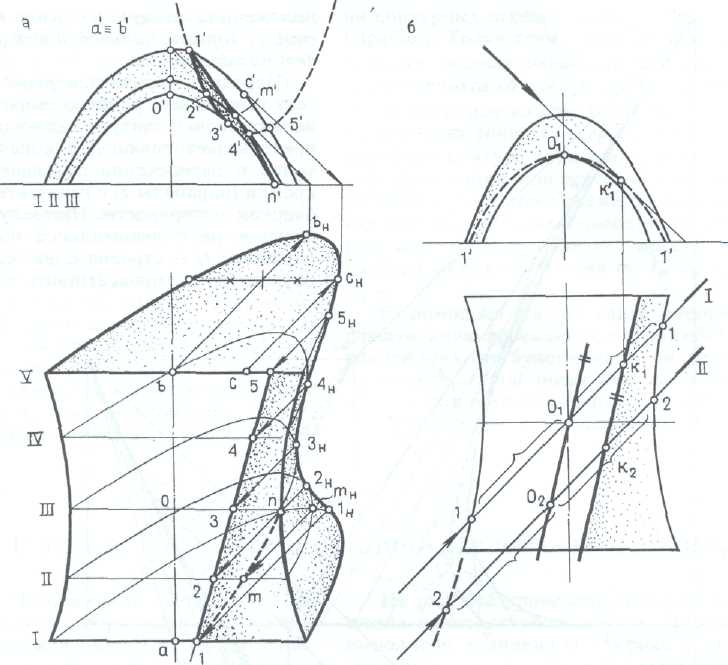
скости или ось симметрии поверхно сти вертикальны, то контуром соб ственной тени явится парабола, рас - положенная в вертикальной плоско­сти, ее горизонтальной проекцией бу­дет прямая линия.

Передняя кромка поверхности бро­сает тень на внутреннюю сторону. На­чальную точку контура падающей тени представляет точка J, а конечную — точка п пересечения падающей тени-кромки (параболы /) с горизонтальным очерком поверхности. Промежуточная точка т на горизонтальной проекции параболы // построена с помощью об­ратного луча, проведенного из точки

пересечения т_н падающих теней пара- бол / и//. Фронтальная проекция тени —- линия I'm п.