Тема 1. Задачи, приводящие к уравнениям различных типов.
Определить тип уравнения с частными производными 2uxx+4uxy+2uyy-2ux+4uy=0.
Решение
Классификация уравнений и принадлежность их к тому или иному типу определяется в зависимости от коэффициентов при старших производных. В общем виде уравнение имеет следующий вид:
=0 (*)
Любое такое уравнение можно привести к каноническому виду. Классификация производится в зависимости от дискриминанта :
Пусть в некоторой области D тогда уравнение называется гиперболическим в D
Если в области D, то (*) называется эллиптическим в D
если во всех точках области D, то уравнение (*)называется параболическим в D.
Определим, к какому классу относится наше уравнение.
2uxx+4uxy+2uyy-2ux+4uy=0
Найдем . следовательно, уравнения параболического типа.
Тема 3. Метод разделения переменных для решения краевых задач.
Однородная прямоугольная мембрана (0
х l, 0
y m),
закрепленная вдоль всего контура,
лежащего в горизонтальной плоскости,
и имеющая в начальный момент форму
U(x,y,0) = (x,
y), начала колебаться с начальной
скоростью
.
Найти закон свободных колебаний мембраны.
Получить решение в случае
,
если натяжение мембраны Т0
равно ее поверхностной плотности ,
т.е.
.
Решение
Предполагая, что мембрана совершает малые колебания, запишем уравнения свободных колебаний мембраны:
,
где
,
(1)
Имеем 1ю краевую задачу с граничными условиями
(3)
(3)
Находим решение методом Фурье:
. (4)
Подставим формулу (4) в уравнение (2), получим .
Разделив это равенство на , имеем ,
Откуда ,(5)
следовательно,
Решение:
, собственные значения , n=1,2…
Также из (5) следует
. (6)
разделим переменные:,
.
Откуда
Решение
собственные значения
, где k=1,2…
Из (6)
Обозначим или ; где , . (9)
Каждой паре номеров , соответствует свое решение .
Решение этого уравнения:
,
где и - произвольные постоянные.
Подставляя найденные , и в (4), получаем все возможные нетривиальные решения уравнения (1), ,
Общее решение:
(10)
Из начальных условий и принципа ортогональности:
и
.
где , a=1
Из этих равенств заключаем, что все числа за исключением коэффициента . А из 2го условия все
Тогда решение
.
БИЛЕТ 11
Тема 1. Задачи, приводящие к уравнениям различных типов.
Найти граничные условия, которые надо наложить на напряжение v(x,t), если известно, что к левому концу провода (x=0) приложена электродвижущая сила E(t), а правый конец (x=l) изолирован.
Решение
Из условия задачи:
Т.к. правый конец изолирован, то
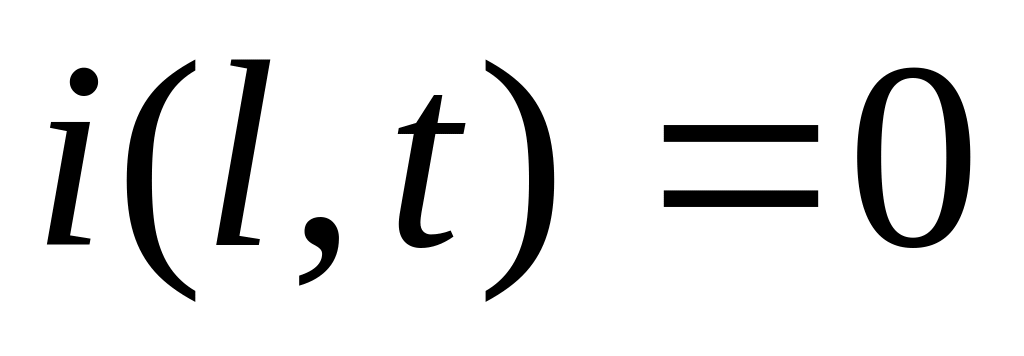
А к левому приложена электродвижущая сила, т.е.
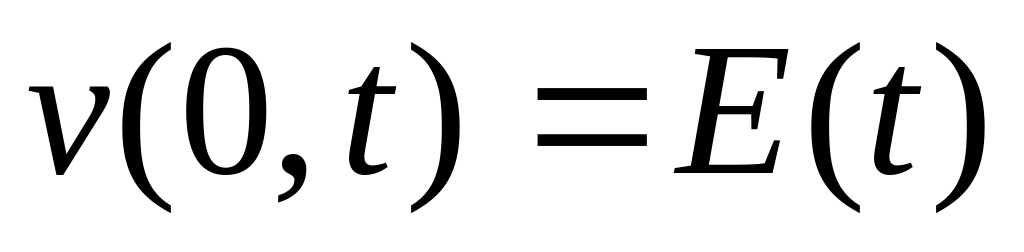(1)
Запишем систему телеграфных уравнений:
Отсюда получим, что
(2)
Таким образом получили (1) и (2) - граничные условия для напряжения v(x,t).
Тема 3. Метод разделения переменных для решения краевых задач.
Решить задачу:
,
;
;
;
.
Решение
Соответствующее однородное уравнение
Решение ищем в классе функций (метод
Фурье):
.
Составим задачу Штурма-Лиувилля:
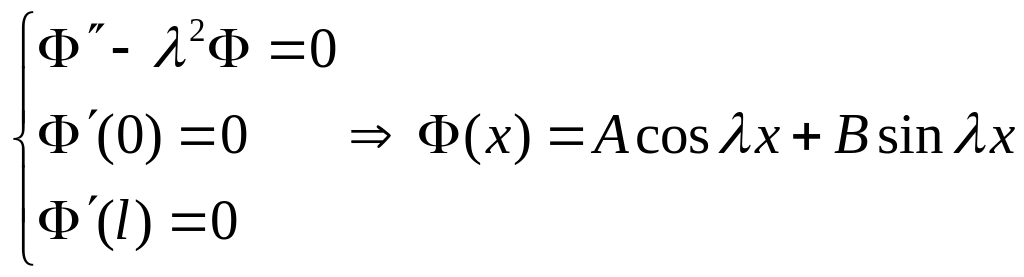
Имеем систему:
Система имеет нетривиальные решения
,
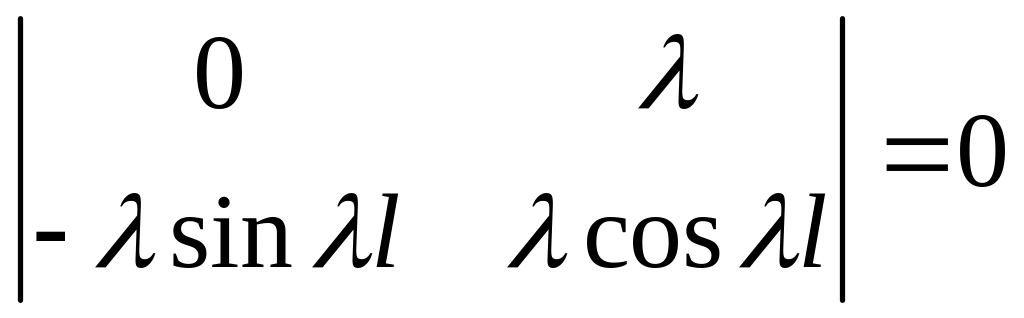тогда собственные функции:
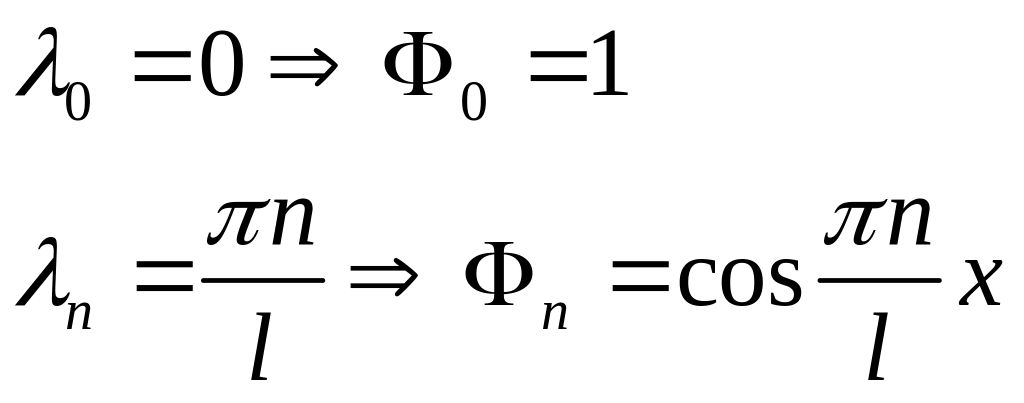
Второе уравнение:
где
.
Решение:
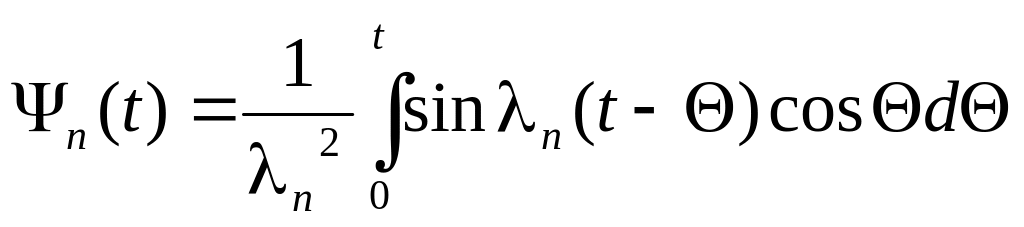
Решение задачи запишем в виде ряда Фурье:
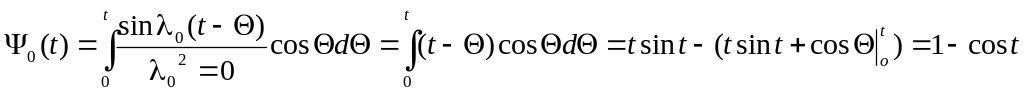и
Конечное выражение:
БИЛЕТ 12