- •Методология объектно-ориентированного анализа и проектирования
- •Семантика кооя, основанная на формальной модели понятия.
- •Описание типов. Примитивные типы и конструкторы типов.
- •Имена понятий. Суррогаты – встроенные системные идентификаторы.
- •Описание типов. Синтаксис тз-спецификаций.
- •Примитивные типы значений и операции над множествами типов.
- •Примеры примитивных типов в различных языках
- •Конструктор декартова произведения “n” типов. Пример спецификации. Селекторы как функции. Селекторы как виртуальные атрибуты.
- •Спецификация рекурсивных типов данных: пример «Бинарное дерево».
- •Задание функций на типах данных («союз», «соединение списков», «сортировка» и т.Д.). Примеры.
- •Логические и модальные утверждения. Пример «Механообработка деталей».
- •База знаний (бз) соз. Машина вывода. Прямая и обратная цепочки рассуждений (понятие, примеры).
- •Многосортное исчисление предметов как язык представления знаний.
- •Альтернативные методы представления знаний: фреймы, семантические сети, продукционные модели.
- •Структура фрейма
- •Графическое представление
- •Математическая запись
- •Семантические отношения
- •Модификации продукционной модели
- •Основные задачи разработки соз.
- •Основы референциальной теории Фреге.
- •Отношение кореференции, семантика имён.
- •Элементы бинарных моделей данных и знаний. Примеры.
- •Темпоральные описания. Интервальная логика событий (Дж. Аллена).
- •Базы знаний и логическое следование. Запросы к бд с неполной информацией.
- •Отличие от баз данных
- •Онтологии и их представлениекак формальная спецификация концептуализации.
- •Агенты для представления знаний.
Логические и модальные утверждения. Пример «Механообработка деталей».
Логические утверждения – это конкретные частные утверждения, заведомо истинные или ложные, иначе говоря, это логические константы.
Простые высказывания назвали логическими переменными, а сложные - логическими функциями. Значения логической функции также только 0 или 1.
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым (или исходным) высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза «И» сложное высказывание также считается ложным.
Дизъюнкция - это логическая операция, которая каждым двум простым (или исходным) высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
Отрицание - логическая операция, которая с помощью связки «не» каждому исходному высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Высказывание, составленное из двух высказываний при помощи связки «если ..., то ...», называется логическим следованием, импликацией.
Высказывание, составленное из двух высказываний при помощи связки «тогда и только тогда, когда», называется эквивалентностью (эквивалентность - логическое тождество, равнозначность, взаимная обусловленность).
Модальная логика — логика, в которой кроме стандартных логических связок, переменных и/или предикатов есть модальности (модальные операторы). Модальности бывают разные; наиболее распространены временны́е («когда-то в будущем», «всегда в прошлом», «всегда» и т. д.) и пространственные («здесь», «где-то», «близко» и т. д.). Например, модальная логика способна оперировать утверждениями типа «Москва всегда была столицей России» или «Санкт-Петербург, когда-то в прошлом, был столицей России», которые невозможно или крайне сложно выразить в немодальном языке. Кроме временных и пространственных модальностей есть и другие, например «известно, что» (логика знания) или «можно доказать, что» (логика доказуемости).
Обычно для обозначения
модального оператора используется ![]() и
двойственный к нему
и
двойственный к нему ![]() :
:
![]()
Это отражает то, что сказать «Москва когда-то была столицей России» то же самое, что сказать «не верно, что Москва никогда не была столицей России».
База знаний (бз) соз. Машина вывода. Прямая и обратная цепочки рассуждений (понятие, примеры).
СОЗ – система основанная на знаниях.
База знаний (БЗ; англ. knowledgebase, KB) в информатике и исследованиях искусственного интеллекта — это особого рода база данных, разработанная для оперирования знаниями (метаданными). База знаний содержит структурированную информацию, покрывающую некоторую область знаний, для использования кибернетическим устройством (или человеком) с конкретной целью. Современные базы знаний работают совместно с системами поиска информации, имеют классификационную структуру и формат представления знаний.
Полноценные базы знаний содержат в себе не только фактическую информацию, но и правила вывода, допускающие автоматические умозаключения о вновь вводимых фактах и, как следствие, осмысленную обработку информации. Область наук об искусственном интеллекте, изучающая базы знаний и методы работы со знаниями, называется инженерией знаний.
Иерархический способ представления в базе знаний набора понятий и их отношений называется онтологией. Онтологию некоторой области знаний вместе со сведениями о свойствах конкретных объектов также можно назвать базой знаний.
Машина вывода — программа, которая выполняет логический вывод из предварительно построенной базы фактов и правил в соответствии с законами формальной логики.
Факт в данном случае — утверждение, являющееся постоянно истинным, например: «Адам является человеком».
Правило в данном случае — параметризованное утверждение, состоящее из двух частей: условия и результата, например: «Если X является потомком человека, то X является человеком». В данном примере правило определяет условие «X является потомком человека». Если для значения параметра X это условие истинно, то правило превращается в факт «X является человеком».
Для построения базы фактов и правил применяются формальные языки, обычно напоминающие естественный язык, но гораздо более строгие и ограниченные.
Машина вывода обычно может выполнять одну или обе из следующих операций:
Проверка истинности некоторого факта — истинным считается факт, если он может быть выведен по законам формальной логики из имеющейся базы фактов и правил.
Нахождение множества значений параметра некоторого правила, при котором данное правило превращается в истинный факт.
В первом случае на вопрос типа «Истинно ли A?» машина вывода даёт ответ «Да» либо «Нет», во втором — на вопрос типа «При каких X истинно правило A(X)?» машина вычисляет все возможные значения X, при подстановке которых в правило A это правило превращается в истинный факт.
На глобальном уровне управления последовательностью применения правил можно выделить две стратегии поведения — применять правила в прямом и обратном порядке. Прямой порядок означает, что цепь рассуждений строится, отталкиваясь от данных (условий, о которых известно, что они удовлетворяются), к гипотезам (состоянию проблемы, вытекающему из этих условий). Обратная цепочка означает, что рассуждения строятся, отталкиваясь от заданной цели (гипотезы, представляющие целевое состояние системы) к условиям, при которых возможно достижение этой цели. Здесь явно чувствуется аналогия с прямой и обратной стратегиями доказательства теорем (см. об этом в главе 8).
Прямая цепочка рассуждений
Суть метода заключается в формировании множества вопросов, позволяющих на каждом шаге отбросить как можно большее число возможных ответов. При этом задаваемые при каждой проверке вопросы целиком зависят от возможных ответов.
При прямом выводе отправной точкой служат предоставленные данные, причем в качестве заключения (если не все дерево пройдено) используется гипотеза, соответствующая самому верхнему уровню дерева (корню).
Для такого вывода характерно большое количество данных, а также оценок дерева, не имеющих прямого отношения к заключению (что излишне)
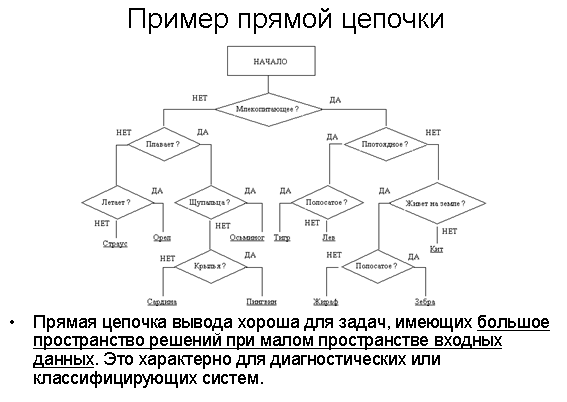
Обратная цепочка рассуждений
Начинают с заключения, которое представляет интерес и не является истинным. Механизм вывода определяет все правила, которые приводят к данному факту как к заключению. Затем рассматриваются посылки этих правил. (В Прологе, механизм вывода основан именно на обратной цепочке рассуждений)
Вводится группа правил высокого уровня. Каждое правило описывает одну категорию, четко указывая, какая информация нужна системе, чтобы прийти к выводу, что именно эта категория является искомым ответом. Система пытается по очереди установить истинность или ложность каждого из правил высокого уровня.