Влияние вида распределения и способа отбора на величину ошибки выборки.
Малая выборка: понятие, особенности проверки гипотез
При использовании больших выборок, сформированных из больших генеральных совокупностей, величина ошибки выборки подчиняется нормальному закону, который устанавливает связь между величиной вероятности и значением t.
Если анализируемая выборка малого объема, то распределение ошибок выборки не подчиняется нормальному закону распределения. Поэтому проблема малой выборки длительное время оставалась нерешенной.
Проблема малой выборки была решена английским математиком и статистиком по фамилии Госсет, который вошел в историю под псевдонимом Стьюдент.
1908 г – доказал, что распределение ошибок в условиях малой выборки подчиняется особому закону распределения, который и получил его имя – t-распределение Стьюдента.
Распределение Стьюдента, как и нормальное распределение, симметрично, однако ветви кривой распределения Стьюдента медленнее приближаются к оси абсцисс. То есть вероятность появления больших отклонений от средней величины в распределении Стьюдента выше, чем в нормальном распределении.
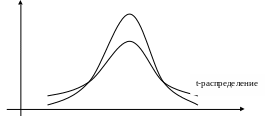
По t-распределению Стьюдента составлены таблицы, в которых (в отличии от нормального распределения) вероятность связана не только с величиной t, но и с числом степеней свободы, которое определяется
d.f. = n – 1 (n – объем совокупности)
При объеме выборки n ≥ 100 значения в таблицах нормального распределения и распределения Стьюдента полностью совпадают, при 30 ≤ n ≤ 100 - расхождения незначительные, при n < 30 - существенные расхождения.
Безусловно малой выборкой считается выборка объемом меньше 30 единиц. Поэтому при работе с выборками таких объемов в формуле предельной ошибки выборки используется величина t из таблицы t-распределения Стьюдента.
В формуле расчета средней ошибки выборки мы не можем игнорировать сомножитель, корректирующий величину выборочной дисперсии.
- в условиях
малой выборки
,
где
S - выборочная дисперсия.
То есть дисперсия делится не на объем выборки, а на число степеней свободы.
Доверительный интервал для разных видов распределения.
Расчет объема выборки.
Расчет объема выборки осуществляют исходя из формулы ошибки выборки. Предельная ошибка выборки:
,
,
,
Величина ошибки выборки обусловлена задачами исследования и задается на стадии проектирования.
Значение t зависит от устанавливаемого уровня вероятности. Значение дисперсии берется по результатам предшествующих аналогичных исследований, если таковые проводились и если за время между исследованиями не произошло существенных изменений в изучаемой совокупности.
Может быть проведено пробное исследование и по результатам его рассчитана величина дисперсии. Но очень часто нет средств на проведение пилотажного (пробного) исследования.
К определению дисперсии подходят формально, исходя их привила трех σ - когда невозможно провести пилотажные исследования.
σ = 1/6 R , где R – размах вариации.
Если распределение заведомо асимметрично, то значение σ = 1/5 R
В формуле расчета объема выборки ( ) ошибка выборки берется как
абсолютная величина, однако, на практике размер ошибки задается, как правило, как относительная величина. То есть говорят, что ошибка не должна превышать 2% (или 5%).
→
Статистическая проверка гипотез.
Ho - Нулевая гипотеза – Гипотеза об отсутствии различий.
H1 - Альтернативная гипотеза – Гипотеза об значимости различий.
Критерий проверки гипотезы: решающее правило, обеспечивающее принятие истинной и отклонение ложной гипотезы с высокой вероятностью
Непараметрические критерии проверки гипотез.
Определение доверительных интервалов для генеральной средней и средней по выборке.
Виды связей между признаками.
Все в этом мире взаимосвязано. Чтобы управлять социально-экономическими процессами и явлениями, необходимо знать наличие, направленность, силу связи между явлениями или признаками.
Существуют два вида связей: