- •Контрольные вопросы
- •Понятие, предмет, задачи статистики.
- •Основные этапы статистического анализа.
- •Ошибки и контроль данных при статистическом наблюдении
- •Группировка в рамках статистического исследования, статистическое представление информации.
- •Понятие вариации, вариационного ряда, показатели вариации
- •Среднее линейное отклонение
- •3. Дисперсия
- •4. Среднее квадратическое (стандартное) отклонение
- •Виды вариационных рядов.
- •1.4.1 Средняя арифметическая простая
- •1.4.2 Средняя арифметическая взвешенная
- •1.4.3 Средняя гармоническая
- •1.4.4 Средняя геометрическая
- •1.4.5 Средняя квадратическая
- •15, 13, 16 Ряды распределения, вариационные ряды, правила их построения.
- •17., 18 Характеристики центра, структуры распределения.
- •Задача сглаживания эмпирического распределения, критерии согласия.
- •Малая выборка: понятие, особенности проверки гипотез
- •Функционально (жестко-детерминированная) связь
- •2) Статистические связи и зависимости (стохастически детерминированная).
- •Показатели тесноты парной связи. Множественная корреляция
- •Коэффициент корреляции
- •Коэффициент детерминации
- •Корреляционное отношение
- •Индекс корреляции
- •Дисперсионный анализ.
- •Цели изучения динамических рядов, их виды, элементы динамического ряда.
- •Компоненты временного ряда.
- •Сглаживание рядов динамики: механическое, аналитическое.
- •Понятие тренда, критерии выбора вида трендовой модели. Оценка качества выбранного тренда.
- •Анализ сезонности в рядах динамики.
- •Абсолютный прирост
- •1. Абсолютный цепной прирост
- •2. Абсолютный прирост базисный
- •Темп роста (коэффициент роста)
- •Темп прироста
- •Абсолютное значение 1% прироста
- •Контроль качества: формы, виды, логика принятия решения о качестве процесса.
- •Статистические индексы, задачи, решаемые с помощью индексного анализа.
- •Индексы общие и индивидуальные. Агрегатный индекс как основная форма индексов.
- •1) Индивидуальные (I)
- •2) Общие индексы (сводные, I)
- •Индексы средние из индивидуальных.
- •Способы расчета индексов.
- •Система показателей статистики цен. Индекс потребительских цен.
- •Индексы Ласпейреса и Пааше.
- •Характеристики уровня жизни населения.
- •Показатели денежных доходов.
- •Показатели дифференциации.
- •Статистические показатели потребления населением материальных благ и услуг.
- •Система статистических показателей инфляции.
- •Статистика населения и занятости.
- •Анализ естественного движения и миграции населения.
- •Индекс развития человеческого потенциала.
17., 18 Характеристики центра, структуры распределения.
Ряды распределения строятся по большим распределениям совокупности. При этом возникает необходимость получить характеристику всего набора данных с использованием одного обобщающего показателя. Прежде всего, таким показателем. Который характеризует совокупность в целом, отражает типический уровень признака в данной совокупности, является средняя арифметическая величина. Среднее рассчитывается на единицу совокупности, однако характеризует совокупность в целом.
По исходным данным средняя величина рассчитывается по средней арифметической простой; если по вариационному ряду – по средней арифметической взвешенной. В качестве весов – частоты, частости. Если среднее рассчитывается по интервальному ряду, в качестве индивидуальных значений признака используются середины интервала.
Мода (M0) – наиболее часто встречающееся значение признаков совокупности.
Проблема расчета данного показателя связана с интервальным вариационным рядом.
Сначала находится модальный интервал (интервал, которому соответствует максимальная частота).
![]() , где
, где
ХМ0о – нижняя граница модального интервала;
h – величина интервала;
fMo – 1 - частота интервала, предшествующего модальному;
fMo – частота модального интервала;
fMo + 1 - частота интервала, следующего за модальным.
Медиана (Ме) – значение признака у единицы, делящей ранжированный ряд пополам.
При определении медианы по ранжированному ряду без группировки
![]()
Если число единиц совокупности четное, то значение медианы определяется как среднее арифметическое двух центральных значений.
Если медиана рассчитывается по интервальному вариационному ряду, то сначала находят медианный интервал, а затем по формуле рассчитывается значение медианы.
Медианный интервал – это первый интервал, в который попадает 50% совокупности.
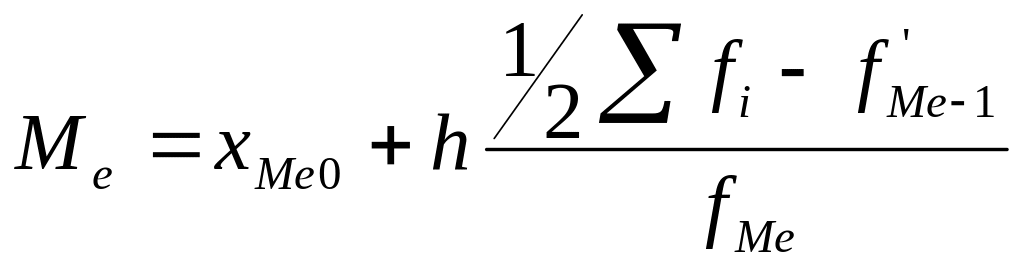 ,
где
,
где
ХМе – нижняя граница медианного интервала;
f’Me-1 – накопленная частота интервала, предшествующего медианному;
fMe – частота медианного интервала;
∑ fi - сумма накопленных частот.
Вопрос выбора показателя центра распределения зависит от типа характеристике, по которой построен ряд распределения, а также от целей исследования.
Если показатель количественный, то могут быть рассчитаны все показатели центра распределения (и средняя величина, и медиана). Тогда выбор показателя зависит от цели исследования и характера изучаемого распределения.
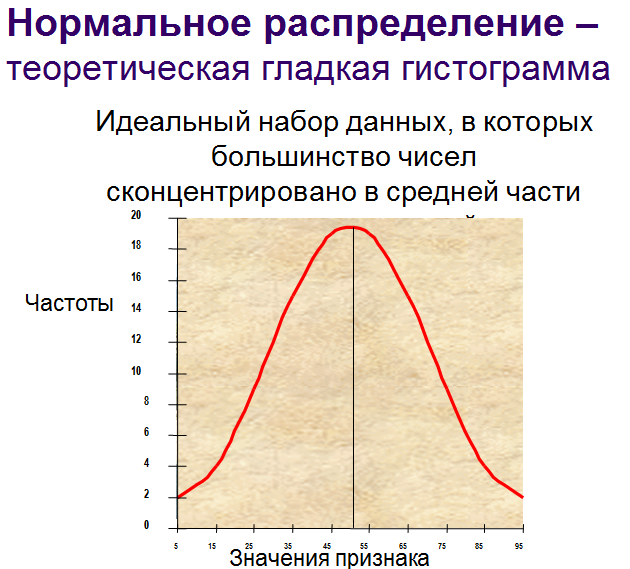
Если распределение соответствует нормальному распределению, то целесообразнее использовать среднюю величину.
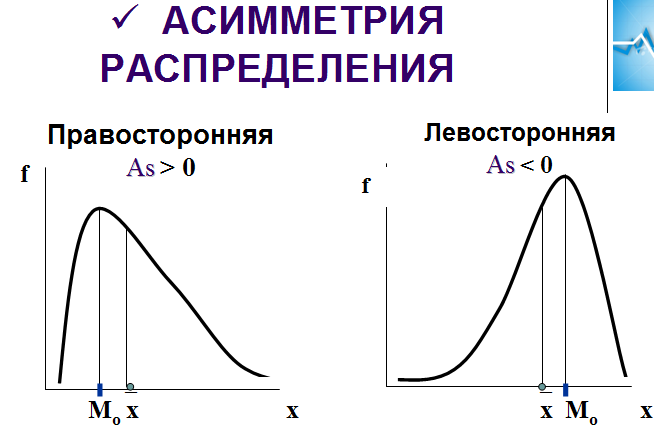
Если в распределении наблюдается существенная асимметрия, то следует использовать либо моду, либо медиану, исходя из цели анализа.
При оценке распределений по атрибутивным признакам, средние значения рассчитаны быть не могут. Показатель моды может быть рассчитан по любому атрибутивному признаку, то есть измерен как по номинальной, так и по порядковой шкале.
Медиана как значение показателя у единицы, делящей ранжированный ряд пополам, одновременно является характеристикой структуры распределения. Так как значение медианы характеризует структуру изучаемой совокупности, указывая, что 50% единиц имеют значение признака меньше медианного, и 50% - больше медианного.
Для более детальной характеристики структуры совокупности, используются такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили – на 10 равных частей, перцентили – ни 100, и другие.
Возможность расчета тех или иных показателей определяется целью исследования и размером изучаемой совокупности.
Перечисленные показатели по интервальному вариационному ряду рассчитываются аналогично расчету медианы. То есть для расчета первого или нижнего квартиля сначала находят квартильный интервал, а затем значение первого квартиля.
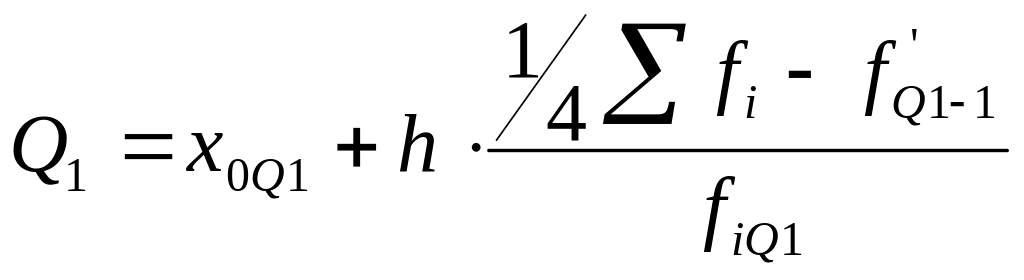 - первый, нижний
квартиль.
- первый, нижний
квартиль.
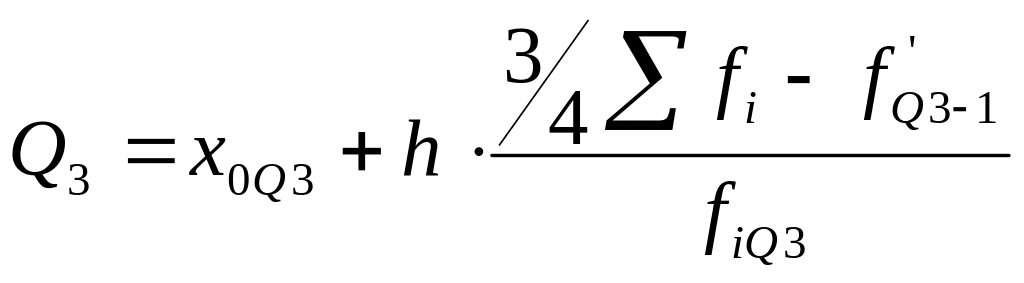 - третий, верхний
квартиль.
- третий, верхний
квартиль.
Значение Q1 означает, что у 25% единиц совокупности значение показателя меньше квартильного, а у 75% - больше.
Значение Q3: у 25% единиц совокупности значение больше данного.
Межквартильное расстояние Q3 - Q1 характеризует размах вариации в центре распределения. На этом интервале находится 50% единиц изучаемой совкупности.
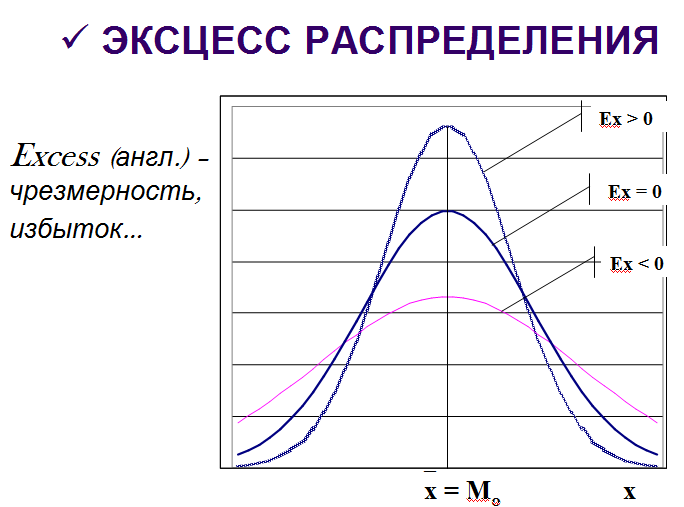
19.Нормальное распределение: понятие и показатели формы распределения.