[Править] Обобщения и модификации

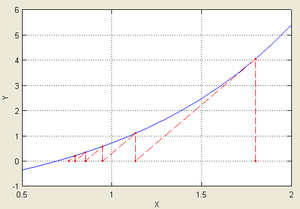
Иллюстрация последовательных приближений метода одной касательной, применённого к функции f(x) = e^x − 2 с начальным приближением в точке x₀ = 1,8.

[Править] Метод одной касательной

В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.

Формула итераций этого метода имеет вид

Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения , а затем использовать это значение на каждой последующей итерации:

.

При таком выборе в точке выполнено равенство

и если отрезок, на котором предполагается наличие корня и выбрано начальное приближение , достаточно мал, а производная непрерывна, то значение будет не сильно отличаться от и, следовательно, график пройдёт почти горизонтально, пересекая прямую , что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.

Этот метод можно также рассматривать, как модернизацию метода хорд (секущих), где число следует выбрать равным .

[Править] Многомерный случай

Обобщим полученный результат на многомерный случай. Пускай необходимо найти решение системы:

Выбирая некоторое начальное значение , последовательные приближения находят путём решения систем уравнений:

,

где .

[Править] Применительно к задачам оптимизации

Пускай необходимо найти минимум функции многих переменных . Эта задача равносильна задаче нахождения нуля градиента . Применим изложенный выше метод Ньютона:

,

где  — гессиан функции .

В более удобном итеративном виде это выражение выглядит так:

Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.

Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.

[Править] Метод Ньютона — Рафсона

Метод Ньютона-Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:

,

где

Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением и обновляют его лишь раз в шагов, либо не обновляют вовсе.

[Править] Применительно к задачам о наименьших квадратах

На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:

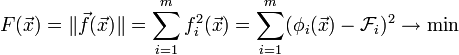
Эти задачи отличаются особым видом градиента и матрицы Гессе:

где — матрица Якоби вектор-функции , — матрица Гессе для её компоненты .

Тогда очередное направление определяется из системы: