
- •21.Резонанс напряжений. Векторная диаграмма.
- •22.Цепь переменного тока с параллельным соединением проводников. Векторная диаграмма.
- •23. Параллельное соединение r, l, с. Векторная диаграмма.
- •24. Резонанс токов. Векторная диаграмма.
- •25. Преобразование последовательного соединения источников и приемников в эквивалентное параллельное и обратно.
21.Резонанс напряжений. Векторная диаграмма.
Резонанс напряжений - резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
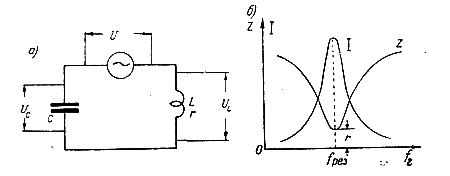
Рис.1 - Схема и резонансные кривые для резонанса напряжений
Резонанс напряжений, или последовательный резонанс, наблюдается в случае, когда генератор переменной эдс нагружен на соединенные последовательно L и С контура (рис.1 а), т.е. включен внутри контура.
В такой цепи имеется активное сопротивление г и общее реактивное сопротивление х, равное
![]()
Разность хL, и xC берется потому, что индуктивное и емкостное сопротивления оказывают противоположные влияния на ток. Первое вызывает отставание по фазе тока от напряжения, а второе, наоборот, создает отставание напряжения от тока.
Для собственных колебаний xL и хс равны друг другу. Если частота генератора равна частоте контура, то для тока, создаваемого генератором, xL и хC также одинаковы. Тогда общее реактивное сопротивление х станет равным нулю и полное сопротивление цепи для генератора равно только одному активному сопротивлению, которое в контурах имеет сравнительно небольшую величину. Благодаря этому ток значительно возрастает и устраняется сдвиг фаз между напряжением генератора и током.
Резонанс напряжений выражается в том, что полное сопротивление контура становится наименьшим и равным активному сопротивлению, а ток становится максимальным.
Условием резонанса напряжений является равенство частот генератора и контура f = fo, или равенство индуктивного и емкостного сопротивлений для тока генератора: xL = хC.
Когда частота генератора больше частоты контура, индуктивное сопротивление преобладает над емкостным и контур представляет для генератора сопротивление индуктивного характера.
Если частота генератора меньше частоты контура, то емкостное сопротивление больше индуктивного и контур для генератора является сопротивлением емкостного характера. В любом из этих случаев при отклонении от резонанса полное сопротивление контура возрастает по сравнению а его величиной при резонансе.
На (рис.1 б) показаны графики изменения полного сопротивления контура z и тока I при изменении частоты генератора f.
22.Цепь переменного тока с параллельным соединением проводников. Векторная диаграмма.
Простейшая параллельная цепь. Рассмотрим простейшую цепь, состоящую из параллельно соединенных активного R и реактивного X сопротивлений (рис. 194,а). В данной схеме в качестве
 Рис.
194. Схема простейшей параллельной цепи
переменного тока (а), векторная диаграмма
(б) и треугольник проводимостей (в)
Рис.
194. Схема простейшей параллельной цепи
переменного тока (а), векторная диаграмма
(б) и треугольник проводимостей (в)
реактивного принято индуктивное сопротивление, но оно может быть также и емкостным. Для каждой ветви этой схемы можно по закону Ома определить токи Iа и Iр в ветвях и их углы сдвига фаз относительно напряжения, а затем, построив векторную диаграмму (рис. 194,б), найти по правилу сложения векторов ток в неразветвленной части цепи:
? = ?а+ ?р
При построении векторной диаграммы в качестве исходного вектора используют вектор напряжения ?, а затем под соответствующими углами откладывают векторы токов ?а и ?р. В данном случае ток ?а будет совпадать по фазе с напряжением ?, а ток ?р — отставать от него на угол 90°. Ток I сдвинут относительно напряжения ? на угол ?.
Из треугольника токов ЛВС имеем:
Iа = I cos ?; Iр = I sin ?; I = ?(I2а + I2р)
Общий случай параллельного соединения сопротивлений. В случае если в каждой ветви включены активное R и реактивное X сопротивления (рис. 195, а), следует по формулам (72) и (73) определить токи I1 и I2 в параллельных ветвях и углы их сдвига фаз ?1 и ?2 относительно напряжения U, а затем, построив векторную диаграмму (рис. 195,б), найти по правилу сложения векторов ток в неразветвленной части цепи ? = ?1+?2 и угол его сдвига фаз ? относительно напряжения U.
Можно также определить эквивалентную активную проводимость всей цепи:
Gэк = G1 + G2
 Рис.
195. Схема параллельной цепи переменного
тока, содержащая активное, индуктивное
и емкостное сопротивления (а), и векторная
диаграмма (б)
Рис.
195. Схема параллельной цепи переменного
тока, содержащая активное, индуктивное
и емкостное сопротивления (а), и векторная
диаграмма (б)
эквивалентную реактивную проводимость
Вэк = ВС2 – BL1
полную проводимость всей цепи
Yэк = ?(Gэк2 + Bэк2)
а затем найти ток в неразветвленной части цепи
I = UYэк
В общем случае при определении эквивалентной реактивной проводимости нескольких параллельных ветвей емкостные проводимости ветвей ВС берут со знаком «плюс», а индуктивные BL — со знаком «минус».
