21. Разложение разностей широт, долгот и азимутов в ряды со средними аргументами

Как отмечено, формулы для решения главной геод. задачи, основанные на рядах с начальными аргументами, имеют ограниченные возможности. Рассмотрим один из возможных путей их усовершенствования, основанный на применении рядов со средними аргументами. При этом мы также будем удерживать в формулах для вычислений малые величины третьего порядка.

Пусть мы имеем некоторую геод. линию s₁₂ ( рис. 6. 2 ), в середине которой имеем точку 0 с координатами B₀ и L₀, геод. расстояния от которой до точек 1 и 2 будут соответственно –s / 2 и s / 2. Действуя аналогично тому, как это делали ранее, запишем следующие разложения для широты:

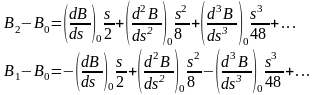
( 6. 9 )

Вычитая из первого уравнения второе, получим

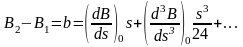, ( 6. 10 )

которое выражает разность широт как и первое уравнение ( 6. 4 ).

Аналогично получаем для разностей долгот и азимутов

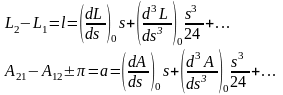( 6. 11 )

Отличие выражений ( 6. 10 ) – ( 6. 11 ) от ( 6. 4 ) состоит в том, что они содержат меньшее число слагаемых и проще для вычислений, но значения производных здесь следует вычислять по широте и азимуту середины линии. Возникает вопрос, быть может эти значения равны средним значениям, получаемым по формулам

B_m=( B₁+ B₂ ) / 2 и A_m= ( A₁₂+ A₂₁ ± π ) / 2.

Проверим, так ли это, для чего возьмем полу суммы уравнений ( 6. 9 ) и аналогичных им уравнений для долгот и азимутов, в результате получим ( 6. 12 )Отсюда видно, что средние коорд. отличаются от координат середины геод. линии на малые величины второго порядка. При этом на данной геод. линии существуют четыре различные точки со средними координатами. Это обстоятельство следует учитывать при дальнейшем выводе рабочих формул.

В формулах ( 6. 10 ) – ( 6. 11 ) коэффициенты разложений представлены производными, являющимися функциями широты и азимута середины геод. линии, значения которых неизвестны. Мы можем вычислить средние широту и азимут, если известны их значения в двух точках. Поэтому перейдем в коэффициентах указанных формул к средним широтам и азимутам ( средним аргументам ). При этом будем иметь в виду порядок малых величин ( 6. 12 ). Для широт имеем

( 6. 13 )

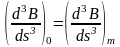( 6. 14 )

Учитывая значения разностей из ( 6. 12 ), выражения для производных, полученные ранее ( 6. 5 ) – ( 6. 8 ), а также вычисляя частные производные

, ( 6. 15 )

получаем для ( 6. 10 ) выражение в виде

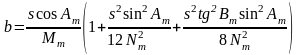( 6. 16 )

Действуя аналогично, получаем для разностей долгот и азимутов

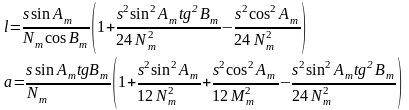( 6. 17 )

Заметим, что в правых частях полученных уравнений ( 6. 16 ) – ( 6. 17 ) дробные выражения, стоящие в скобках, являются малыми величинами третьего порядка, их можно для удобства вычислений с принятой точностью принять равными главным членам разложений и тогда можем записать

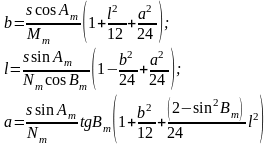( 6. 18 )

Здесь вычисления ведутся в радианной мере, а в последнем уравнении, в поправочном члене принято

a = lsinB_m. ( 6. 19 )