23. Частотные критерии качества

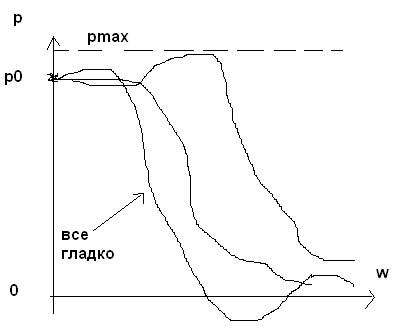
Эти методы не предусматривают вычисления р(t)? А основаны на анализе частот хар-к , поэтому явл косвенным , потому и носят название критериев .Рассм вещ-частотные хар-ки

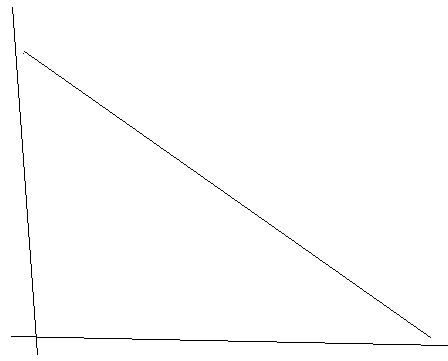
ВЧХ:

Pmax –мах знач веществ части

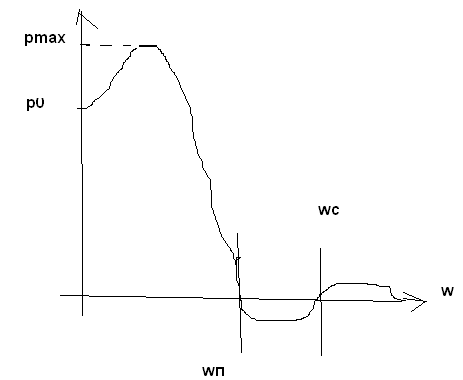
w>wc область несуществ частот

wп –обл перехода

1. Двум сист с близ ВЧХ соотв близкие их перех проц, последовательные и одинак показатели кач-ва

2 Интервал несуществ частот w>wc влияет на перех ф-ю Н(t), но только в начале при малых t

3. Если две сист имеют разн ВЧХ но подобн по форме, то масштобирование можно свести к аналогичным и вых процессы.

А)

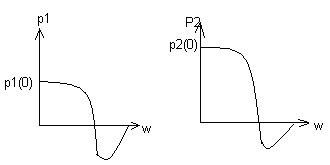
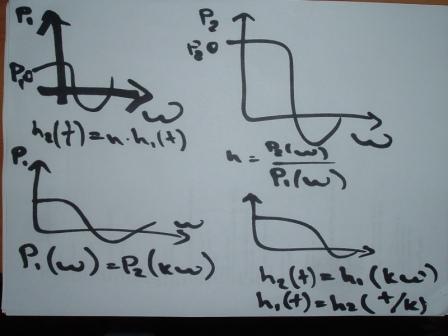
h (t)= h*h (t), где n=

Б) графики те же P (w)= P (kw)

h (t)= h (k*t), h (t)=h

Это позвол опред показат качества по аналогии

4. Лин сист отвеч принципу аддитивности

Если P(w)= h(t) = (t)

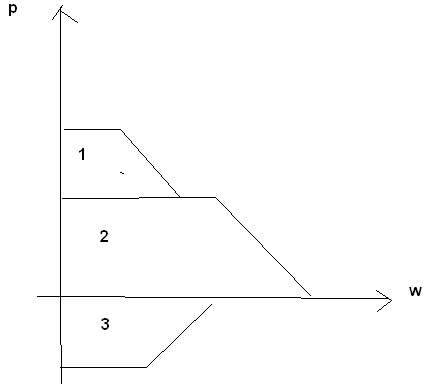
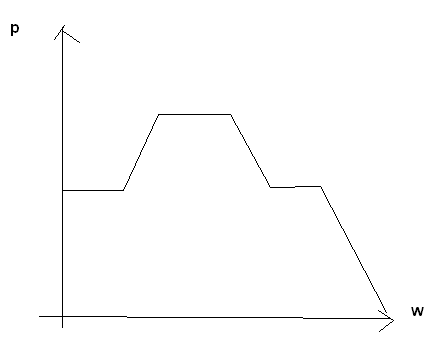
На этом принципе основан метод трапеции для расчёта вых хар-к

5 опред колебательности

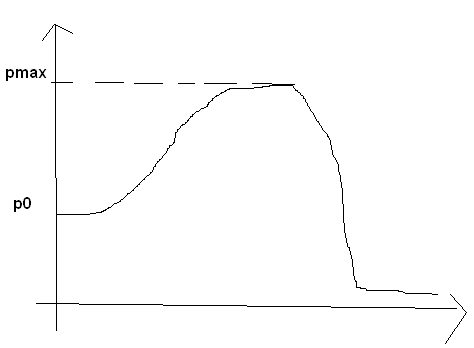
M=

6. Опред перегруппирования

Если х-ка невозраст

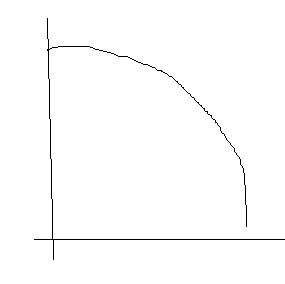
Если монот-убыв

если вид

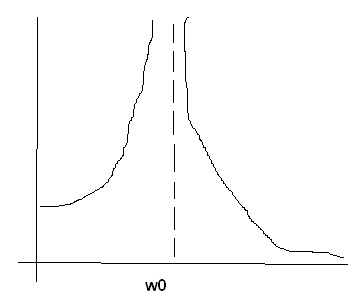то сист нах на границе устойч

7. Время регулир чем шире хар-ка по w тем выше быстродейств сист, чем уже хар-ка , тем меньше быстродействие системы.

Используя ВЧХ можно использ св-ва системы по аналогии с объектом , св-ва которого же известны .

24. Интегральные критерии качества переходных процессовСау.

Предъявив к перех процессу всё более жёсткие требования , мы можем перейти к образцовому , базовому перех процессу- .Если сущ-ет шаблон понятие – траектория , подразумевая под ней как просто перех ф-ия , так и пространственная , то оценка качества сводится к оценки близости , совпадения с этой траекторией Надо интегрировать по всей траектории либо по независимому параметру

Если траектория h (t), то

- мера качества.

Такой и подобные интегралы и явл интегральн критериями (это накопленная оценка на всеё территории) . var = J 0 / Такие ф-ии наз функуионалами (определённые интегралы)

S= функционал

Использ функ-лы различ порядков, определяющих сложность критерия

J=

F – нейкий вид преобразователей над исх ф-ией f(t)

T= f(t) хар-ет перех процессы , но f(t) h(t)

В простом случае f(t)=hуст-h(t)=y (отличие некоторого процесса от некот эталона)

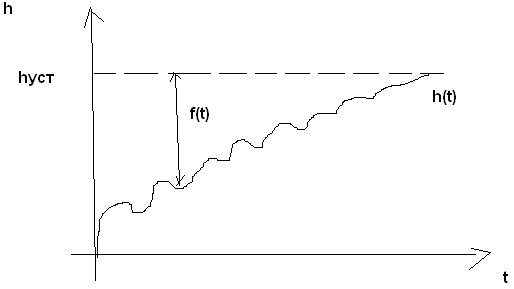
В зависимости от F будут разл интегральные оценки. Самые простые

линейные оценки (лин функционалы)

S=

- взвешивающая ф-ия

Обобщённая линейная оценка

S =

Рассм несколько таких оценок

S = . Такая оценка пригодна для монотонных процессов

S = - первый момент распр f(t)

S - проекция центра тяжести на ось t

S = . Набор таких моментов S ……..S явл более простым . этот подход наз методом моментов .Для колебательных перех процессов исп-ся квадратичные оценки.

J = J =

Квадрат оценка более универсальная . Если построена эталон ф-ия , то достаточно 0 и 1-го порядка , чтобы вычислить эталон .

25. Осн. Особен. Нелин. Сау

Уравнения связывающие вход и выход могут быть нелинейными уравнениями. Если нелинейность небольшая,то можно линеоризировать систему. Если в САУ есть хотя бы одно звено имеющее существенную нелинейность, то система нелинейна.

Обычно линейную часть можно выделить.

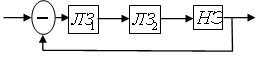
Все нелинейности делятся на два класса:

• Однозначные – однозначная связь между входным и выходным сигналом.

• Неоднозначные – если система зависит не от одной однозначной связи входа к выходу, а и от, например, изменения t в сторону + или - .