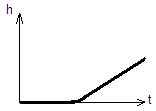
- •Основной принцип автоматиз-ого упр-ния – в каждый момент t анализ-ся y(t) и срав-ся с требуемым знач. И на основании сравнения делается вывод о режиме дальнейшего упр-ния.
- •Сигналы в системах автоматического управления.
- •Основные принципы управления и требования к сау.
- •Прямое и обратное преобразование Лапласа, основные свойства, примеры преобразований.
- •Дифференциальная и операторная формы уравнений сау.
- •Передат. Ф-ция динамич. Системы. Свойства передаточной функции.
- •Частотные хар-ки сау и их взаимосвязь
- •Типовые входные воздействия и временные характеристики сау.
- •Типов. Звенья сау: нейтральн. Звенья.
- •Типовые звенья сау: инерционные звенья
- •Типовые звенья сау: форсирующие звенья
- •Особые звенья сау: неминимально-фазовые и неустойчивые звенья.
- •Особые звенья сау: иррациональные и трансцедентные звенья.
- •Соединения звеньев сау: виды, передаточные ф-ции и св-ва объединённых звеньев.
- •Эквивалентные преобразования структурных схем сау
- •Устойчивость линейных сау. Аналитический метод определения устойчивости.
- •Алгебраический критерий устойчивости Гурвица
- •Частотн. Крит. Михайлова.
- •Частотный критерий Найквиста (для статических систем).
- •Частотный критерий Найквиста (для астатических систем).
- •Качество сау. Показатели качества. Точность систем управления.
- •Аналитечный (прямой) метод определения качества сау.
- •Частотные критерии качества
- •Интегральные критерии качества переходных процессовСау.
- •Осн. Особен. Нелин. Сау
- •Основные особенности нелинейных сау.
- •Основн источники нелин-тей и типов нелин звенья сау.
- •Динамич анализ нелин сау:метод Попова.
- •Фазовый метод:фазов простр-во,построен-е троекторий.
- •Применение метода фазовых траекторий для анализа устойчивости систем управления.
- •Сущность метода гармонического баланса (применительно к нелинейной сау).
- •Анализ динамической устойчивости сау методом гармонического баланса.
- •Принципы построения дискретных и цифровых сау. Дискретизация и квантование непрерывного сигнала.
- •Дискретное преобразование Лапласа и z-преобразование. Получение z-передаточной функции цифровой сау.
- •Идеальный и реальный дискретизаторы цифровых сау.
- •Анализ устойчивости цифровой сау по z – передаточной ф-ии
- •Анализ устойчивости цифровой сау с использованием биленейного конформного преобразования
Типов. Звенья сау: нейтральн. Звенья.
Нейтральные звенья – это такие звенья, предат. хар-ка которых опис-ся ур-ем:
1) W(p)=k
2)
![]()
Это значит, что степень числителя и знам-ля при p одинакова.
![]() – постоянная
времени звена
– постоянная
времени звена
Это звено явл. минимально-фазовым. К этим звеньям относятся те нули передаточных функций, которых находятся в левой полуплоскости. Они имеют минимальное значение фазы. Они все устойчивые и легче всего физически реализуемы.
Типовые звенья сау: инерционные звенья
![]() -
инерционное звено 1-го порядка
(интегрирующее)
-
инерционное звено 1-го порядка
(интегрирующее)
p->jw
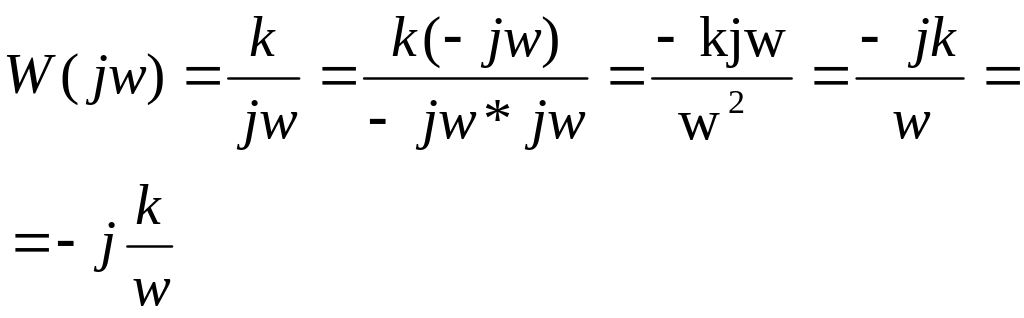
![]()
![]()

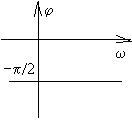
Годограф:
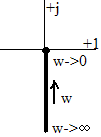
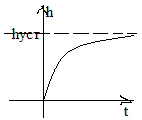

Инерционные звенья 2-го порядка:
![]() -
каноническая форма записи колебательного
звена,
-
каноническая форма записи колебательного
звена,
с - показатель колебательности
Если знаменатель
ур-ия прировнять к нулю, и находятся
корни, то полином м.б. разложен на
произведение 2-х полиномов:
![]() ,
а это значит, что это последовательное
соединение 2-х звеньев. Его нужно сводить
к более простым.
,
а это значит, что это последовательное
соединение 2-х звеньев. Его нужно сводить
к более простым.
Если с=0, то
![]() звено
явл. колебательным, но не затухающим,
такое звено назыв. стационарным.
звено
явл. колебательным, но не затухающим,
такое звено назыв. стационарным.
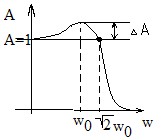
![]() - величина усиления
резонанса
- величина усиления
резонанса
![]() -
резонансная частота
-
резонансная частота
![]()
Чем выше с, тем быстрее затухают колебания
Приближенная ЛАЧХ:
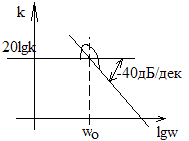
Еще один вид
инерционных звеньев 1-го порядка –
апериодическое:
![]()
Типовые звенья сау: форсирующие звенья
Форсирующее звено I пор.:
![]()
![]() -
const
-
const
![]()
![]()
![]()
![]()
Это звено не явл. устойчивым
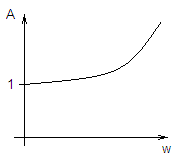
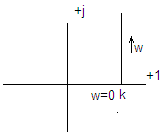
Могут существовать как элементы, дополняющие систему
Форсирующее звено II пор.:
![]()
![]()
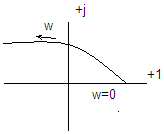
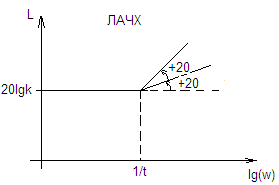
![]()
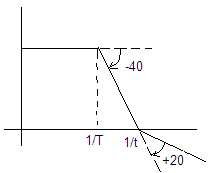
сначала
на -40 потом на +20 или наоборот, в зависимости
от того, что больше 1/Т или
![]()
![]() -упругое
звено (инерционно-форсирующее)
-упругое
звено (инерционно-форсирующее)
ЛАЧХ
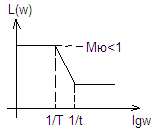
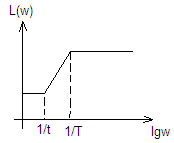
![]()
![]() <1
– в большей степени инерционно
<1
– в большей степени инерционно
>1 – звено более форсировано
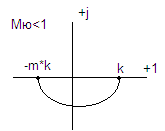
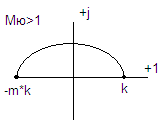
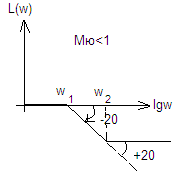
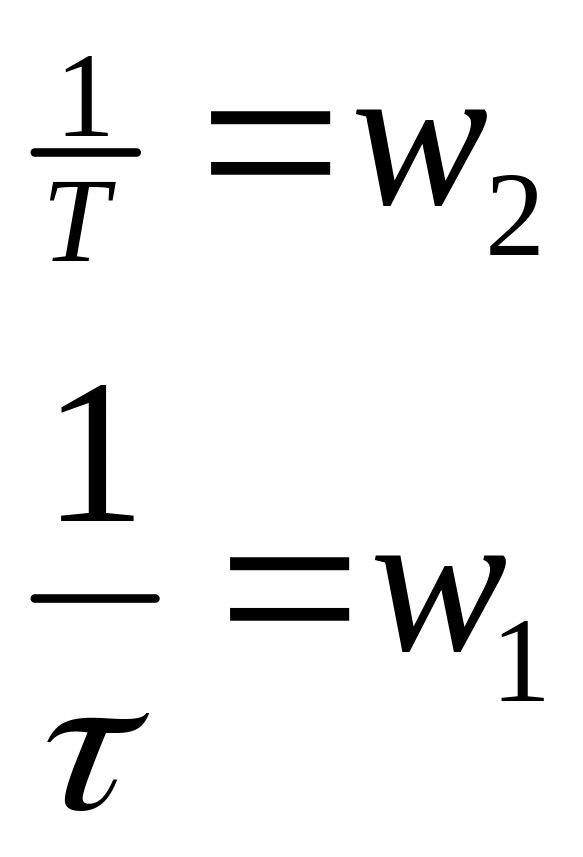
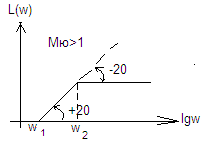
Дифференцирующее звено относится к форсир. звеньям I пор.
W(p)=kp – идеальное
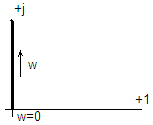
Особые звенья сау: неминимально-фазовые и неустойчивые звенья.
Все звенья имеют слабое применение как отдел. динамич. системы, т.к. они плохо управляемы либо не управляемы, но они могут входить в состав системы в целом, т.е. управляться типовыми звеньями.
Неминимально-фазовые (I пор.)
![]()
Звено будет иметь большую фазу, неминим.
АЧХ идентичны миним.-фазовым.
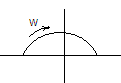 Такое
звено может оказаться неустойчивым.
Такое
звено может оказаться неустойчивым.
Неустойчивые (II пор.)
Полюсы положительны. Такое звено всегда неустойчиво.
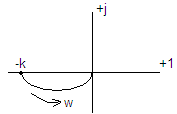
Особые звенья сау: иррациональные и трансцедентные звенья.
Иррациональные
![]() -полуинтегрир.
звено
-полуинтегрир.
звено
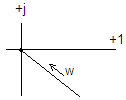 ЛАЧХ
будет иметь наклон 10 ДБ/дек
ЛАЧХ
будет иметь наклон 10 ДБ/дек
![]() -полуапериод.
звено I
рода
-полуапериод.
звено I
рода
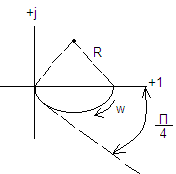
![]() -полуапериод.
II
рода
-полуапериод.
II
рода
![]() - полуфорсир. I
рода
- полуфорсир. I
рода
![]() - полуфорсир. II
рода
- полуфорсир. II
рода
![]() - полудифф.
- полудифф.
Объекты, в кот. проходит теплопроводность или диффузия явл. полуинерц.
Трансцедентные
Трансцедент. ф-ции – это показат. ф-ции е в степени. Такие уравнения не явл. полиномами, но могут быть отнесены к линейным звеньям.
![]() A(w)=const=1
A(w)=const=1
![]()
![]()
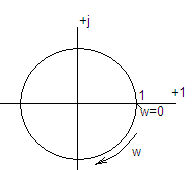 - годограф этого
звена
- годограф этого
звена
![]()
Трансцедент. звено наз. звеном запаздывания.
![]() - такое звено будет
звеном полузапаздывания или звено
замедления.
- такое звено будет
звеном полузапаздывания или звено
замедления.
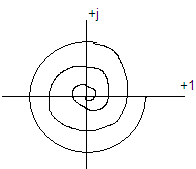
Переходная функция h(t) для окружности:
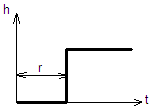
h(t) – для замедления: