15 Евклидовы пространства. Определение, примеры

ОПР: скалярное произведение двух векторов а и b в линейном пространстве L над полем Р - действительное число. Обозначается (а, b) и удовлетворяет следующим аксиомам:

1 (а, b) = (b, а) для любого а, b принадлежащего L

2 ((а + b), с) = (а, с) + (b, с) для любых а,b,c принадлежащих L

3 ((αa), b) = α (а, b) для любого а, b принадлежащего L, для любого α принадлежащего R

4 (а, а) ≥ 0, (а, а)= 0 в том и только том случае, если а = 0

Следстивие 1: для любых а,b,c принадлежащих L (а, (b + с)) = (а, b) + (a, с)

Доказательство:

(а, (b + с)) = 1)= ((b + с), а)= 2)= (b, а) + (с, а) = 1)= (а, b) + (a, с) чтд

Следствие 2: для любого а, b принадлежащего L, для любого α принадлежащего R

(а, αb) = α (а, b)

Следствие 3.

Пример.

Опред. Линейное пр-во L над полем R наз Евклидовым, если в нём определена операция скалярного произведения.

Замечание. В пр-ве L над полем С также может быть введено понятие скалярного произведения, в соответствие ставится комплексное число(такое пр-во наз комплексным Евклидовым или унитарным) и изменяется 1-я аксиома /

Т. В любом Евклидовом пр-ве справедливо нер-во Каши-Буняковского

Следствие.

16. Свойства скалярного произведения, длина вектора, угол между векторами

Опред. Скалярным произведением 2-х векторов a, b в пр-ве над будем называть действительное число, кот. уд . следующим аксиомам:

1. 

2. 

3. 

4. 

Длиной вектора а в пр-ве над R наз. ; в : ; C : .

Углом между векторами в произвольном Евклидовом пр-ве наз. угол , .

17. Ортонормированные системы векторов.

Опр. 2 вектора a,b в пр-ве наз ортогональными, если .

Лема. Если некоторый вектор A ортогонален всем векторам пр-ва E, то это нулевой вектор.

, ,

Т. Ортогональные сис-мы ненулевых векторов линейно-независимы.

Опр. Сис-ма векторов наз ортонормированной если она ортогональная и все векторы имеют единичную длину.

Т. В любом конечном Евклидовом пр-ве сущ ортонормированный базис.

18. Метод ортогонализации Грамма – Шмидта.

Процесс построения ортогонального базиса к конечномерном Евклидовом пр-ве наз методом ортоганализации Грамма-Шмидта

В пр-ве многочленов не выше 2-й степени, требуется построить ортогональный базис на .* *

,

Сис-ма: .

19. Выражение скалярного произведения через координаты перемножаемых векторов. Матрица Грамма. 

Теорема. Если векторы a и b заданы своими координатами:a={X₁;Y₁;Z₁}, b={X₂;Y₂;Z₂}, то скалярное произведение опред. Формулой

ab=X₁X₂+Y₁Y₂+Z₁Z₂.

Скалярное произведение двух векторов равно сумме попарных произведений соответствующих координат этих векторов.

Следствие1. Необходимым и достаточным условием перпендикулярности векторов a и b является равенство: X₁X₂+Y₁Y₂+Z₁Z₂=0

Следствие2. Угол между векторами находится: cos f=

Слдствие3. Пр_us=XcosJ+YcosB+ZcosY

Определителем Грама системы векторов e₁, e₂, ..., e_n в евклидовом пространстве называется определитель матрицы Грама этой системы:

где   — скалярное произведение векторов e_i и e_j.

Матрица Грама возникает из следующей задачи линейной алгебры:

Пусть в евклидовом пространстве V система векторов e₁, e₂, ..., e_n порождает подпространство U. Зная, чему равны скалярные произведения вектора x из U с каждым из этих векторов, найти коэффициенты разложения вектора x по векторам e₁, e₂, ..., e_n. Исходя из разложения x = x₁e₁ + x₂e₂ + ... + x_ne_n получается линейная система уравнений с матрицей Грама:

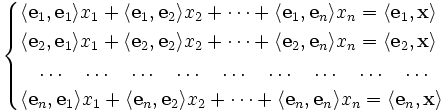Эта задача однозначно разрешима тогда и только тогда, когда векторы e₁, e₂, ..., e_n линейно независимы. Поэтому обращение в нуль определителя Грама системы векторов - это критерий их линейной зависимости.

20. Нормированные векторные пространства. Векторное пространство  называется нормированным, если на его элементах определено отображение , называемое нормой, которое удовлетворяет следующим аксиомам:

1)  ;

2)  ;

3)   

21. Ортогональные матрицы и их свойства. 

Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на A^T равен единичной матрицеAA^T = A^TA = E,или, что эквивалентно, её обратная матрица равна транспонированной матрице:

• Свойства. Столбцы и строки ортогональной матрицы образуют системы ортонормированных векторов, то есть:

где  , n — порядок матрицы, а δ_jk — символ Кронекера.

Другими словами, скалярное произведение строки на саму себя равно 1, а на любую другую строку — 0. Так же и для столбцов.

• Определитель ортогональной матрицы равен  , что следует из свойств определителей:

• Множество ортогональных матриц порядка n над полем k образует группу по умножению, так называемую ортогональную группу которая обозначается O_n(k) или 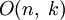  (если kопускается, то предполагается  ).

• Ортогональные матрицы соответствуют линейным операторам, переводящим ортонормированный базис линейного пространства в ортонормированный.

• Любая вещественная ортогональная матрица подобна блочно-диагональной матрице с блоками вида

 и