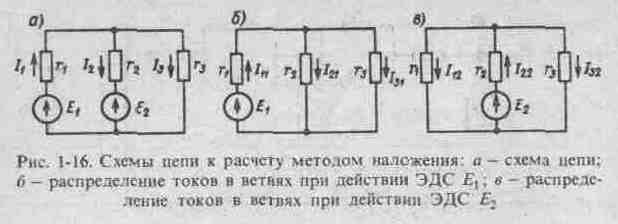
Расчет электрической цепи методом наложения. Дать расчет простейшей цепи.
При расчете по методу наложения ток в любой ветви электрической цепи определяется как алгебраическая сумма токов, вызываемых в данной ветви каждой из ЭДС в отдельности, в предположении равенства нулю всех остальных ЭДС.
Рассмотрим расчет
по методу наложения на примере. Определим
токи в ветвях цепи при наличии только
ЭДС
и
.
Токи в ветвях
определятся выражениями:
.
Токи в ветвях цепи
при действии одной ЭДС
Токи
в ветвях определятся как алгебраические
суммы токов, вызываемых каждой из ЭДС
в отдельности, например
.
Здесь ток
вычитается из
тока
потому, что направление тока
обратно
направлению тока
,
принятому за положительное.
Метод наложения несколько громоздок и неудобен для расчета. Вместе с тем в ряде случаев применение этого метода позволяет быстро определить ток в одной ветви, исследовать влияние изменения одной из ЭДС на изменения токов в ветвях и решить другие задачи.
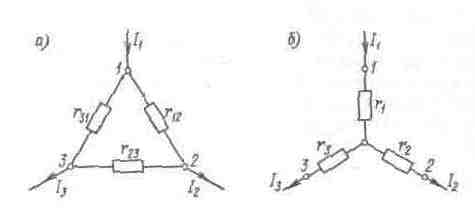
Преобразование электрических схем с треугольника в звезду и наоборот.
Очень важными приемами являются преобразование соединения звездой в соединение треугольником и обратное преобразование.
Соединение звездой получается при объединении начал Н или концов К резисторов в одну точку. На рис. 1-18, а показана трехлучевая звезда резисторов. Резисторы могут располагаться и произвольно на плоскости рисунка, как это показано, например, на рис. 1-18,б.
Если конец каждого резистора соединить с началом последующего и конец последнего резистора — с началом первого, получим соединение многоугольником. Резисторы можно соединять в любом порядке. Обычно три резистора при соединении треугольником располагают на рисунке вдоль сторон правильного треугольника (рис. 1-19, а). Резисторы могут располагаться и произвольно, как показано на рис. 1-19,6, так как важен только способ соединения.
В ряде случаев необходимо для упрощения цепи преобразовать соединение звездой в эквивалентное соединение треугольником или соединение треугольником — в соединение звездой.
Предположим, что
в сложную цепь входит группа резисторов
и
,
соединенных треугольником и присоединенных
к точкам 1,2 и
3 внешней
цепи (рис. 1-20, а).
Требуется заменить это действительно
существующее соединение треугольником
эквивалентным соединением звездой. Для
этого нужно определить значения
сопротивлений резисторов
и
(рис. 1-20,6), входящих в звезду, так, чтобы
проводимости между точками 1
и 2; 2 и 3; 3 и 1
внешней цепи остались без изменения.
Например, проводимость между точками
1
и 2 присоединении звездой является
обратной величиной суммы сопротивлений
между этими точками
,
а проводимость при соединении треугольником
равна сумме проводимостей
двух
параллельных ветвей 1—2
и 1—3— 2:
.
Приравняем эти проводимости:
.
Преобразовывая
три равенства для проводимостей в три
равенства для сопротивлений
и
,
получим
Решая эти три уравнения относительно неизвестных сопротивлений , получим
Решение той же системы уравнений относительно сопротивлений и , определяет возможность замены в эквивалентной схеме звезды сопротивлений и треугольником сопротивлений и , которые получаются равными соответственно:
В
ряде случаев применение указанных
преобразований сразу решает задачу
расчета сложной цепи. Например, используя
преобразование звезды в треугольник
применительно к схеме рис. 1-21,а,
получим схему рис. 1-21,6, представляющую
собой комбинацию параллельных и
последовательных соединений сопротивлений.
