
- •Министерство образования и науки российской федерации
- •Кемерово 2012
- •Выбор номеров задач контрольной работы
- •Методические указания к контрольной работе
- •3. Теория функций комплексного переменного
- •3.1. Комплексные числа и действия над ними.
- •3.2. Алгебраические действия над комплексными числами.
- •4. Обыкновенные дифференциальные уравнения
- •Дифференциальные уравнения первого порядка
- •Общее решение однородного уравнения
- •Частное решение неоднородного уравнения
- •Обыкновенные дифференциальные уравнения
- •Список рекомендуемой литературы
3.2. Алгебраические действия над комплексными числами.
Для выполнения алгебраических действий над комплексными числами (№ 91-120) необходимо проработать литературу: [1, т. 1, гл. VI, § 3, с. 137, 138; 3, т.2, § 5.3, с. 239-244], где содержатся теоретический материал и практические рекомендации по данной теме.
Сложение
и умножение
комплексных чисел производится по
правилам сложения и умножения
алгебраических многочленов с учетом
![]() .
При записи результата следует отделить
действительную часть от мнимой, т. е.
собрать отдельно члены, содержащие
множитель
.
При записи результата следует отделить
действительную часть от мнимой, т. е.
собрать отдельно члены, содержащие
множитель
![]() ,
и члены, не содержащие множитель
,
и члены, не содержащие множитель
![]() :
:
![]()
![]()
![]()
В
частности,
![]() .
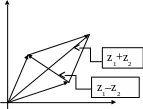
Операции сложения и вычитания сводятся
к сложению и вычитанию векторов,
изображающих эти числа. Отсюда расстояние
между точками
.
Операции сложения и вычитания сводятся
к сложению и вычитанию векторов,
изображающих эти числа. Отсюда расстояние
между точками
![]() .
.
y
z1
z2
z1+z2
Рисунок 6 |
Пример 5.
и
радиусом равным
Деление на комплексное число, отличное от нуля, определяется как действие, обратное умножению. |
Для
представления частного в виде
![]()
следует провести простые преобразования, показанные на следующем примере.
Пример
6.
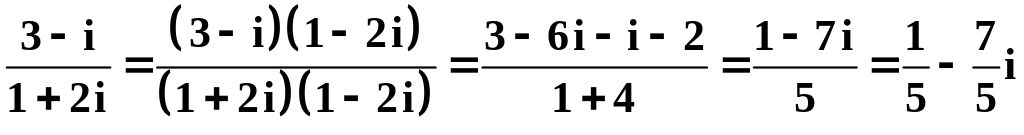 .
.
Для модуля и аргумента произведения и частного справедливы следующие утверждения:
1.
![]()
Пример
7. Найти
модуль и аргумент произведения
![]() .
.
Решение.
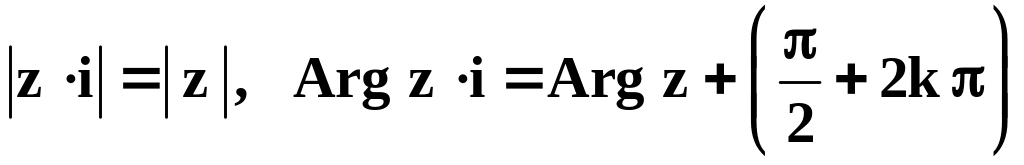 .
.
Таким
образом, умножение на
соответствует повороту вектора
![]() на угол;
на угол;
2.
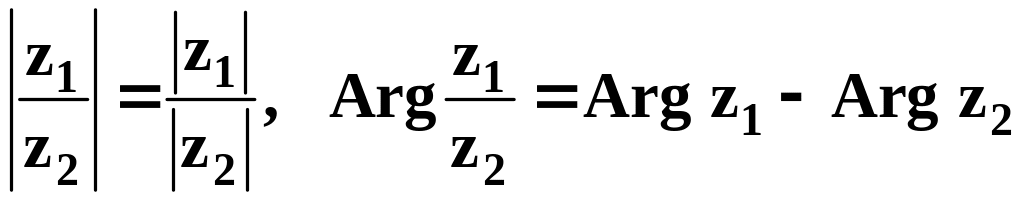 .
.
Пусть
![]() .
.
Тогда
![]() .
.
Можно
доказать методом полной математической
индукции, что для любого целого
![]() (формула Муавра). Формула справедлива
и для целых отрицательных
(формула Муавра). Формула справедлива
и для целых отрицательных
![]() .
.
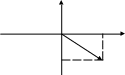
Пример
8. Вычислить
![]() .
.
0 x
-1 z Рисунок 7 |
Решение
|
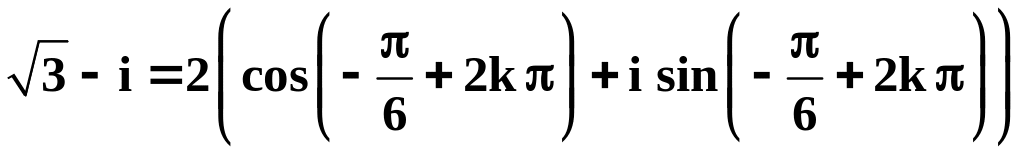 ,
,
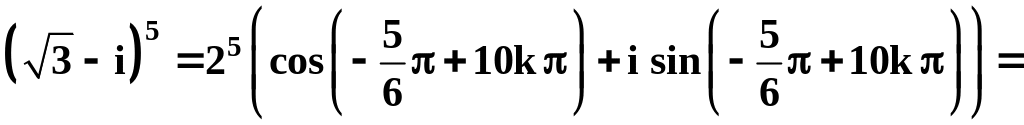
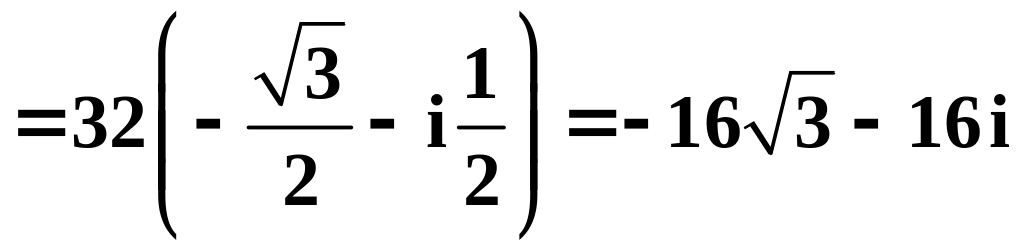 .
.
Корнем
![]() -й
степени из комплексного числа называется
такое число
-й
степени из комплексного числа называется
такое число
![]() ,
для которого
,
для которого
![]() .
.
Используя формулу Муавра, получим
![]()
Для
других значений
![]() аргументы будут отличаться от полученных
на число кратное
,
и, следовательно, получатся значения
корня, совпадающие с рассмотренными.
Итак, корень
-й
степени из комплексного числа имеет
различных значений.
аргументы будут отличаться от полученных
на число кратное
,
и, следовательно, получатся значения
корня, совпадающие с рассмотренными.
Итак, корень
-й
степени из комплексного числа имеет
различных значений.
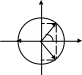
Пример
9. Найти все
значения
![]() и построить их.
и построить их.
Рисунок 8 |
Решение.
|
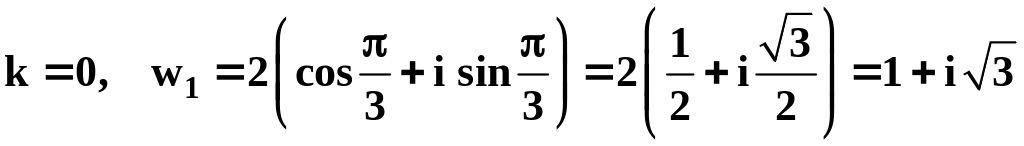 ,
,
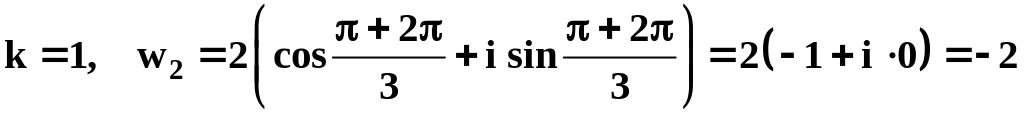 ,
,
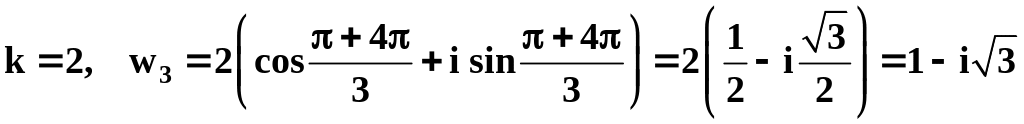 .
.
4. Обыкновенные дифференциальные уравнения
В задачах № 91-120 при отыскании общего решения дифференциального уравнения первого порядка следует использовать литературу [2, т. 2, гл. VI, § 3, 4, с. 161 - 166; 4, п. 12.5-12.8, с. 169-277].
Перед решением задач нужно определить тип уравнения и метод решения, при этом можно руководствоваться табл.1.
Пример.
Найти общее решение уравнения
![]() .
.
Так
как
![]() ,
то получаем уравнение
,
то получаем уравнение
![]() – уравнение первого типа. Разделяем
переменные
– уравнение первого типа. Разделяем
переменные
![]()
где
– произвольная постоянная. Можно
оставить решение в таком виде или
выразить
![]() в явном виде
в явном виде
![]() .
.
Пример.
Найти общее решение уравнения
![]() .
.
Это
уравнение второго типа, однородное,
следовательно, делаем подстановку
![]() .
Уравнение примет вид
.
Уравнение примет вид
![]() .
.
Получили уравнение с разделяющимися переменными
![]() .
.
Здесь
мы обозначили произвольную постоянную
не
,
а
![]() для удобства записи
для удобства записи
![]() .
.
Можно оставить решение в таком виде, а можно выразить явно
![]() .
.
Пример.
Найти общее решение уравнения
![]() .
.
Это
линейное уравнение
![]() (табл.1). Делаем подстановку
(табл.1). Делаем подстановку
![]() .
Подставив эти соотношения в исходное
уравнение, получаем
.
Подставив эти соотношения в исходное
уравнение, получаем
![]() .
Одну из функций находим из уравнения
.
Одну из функций находим из уравнения
![]() ,
,
тогда
вторая функция
![]() определяется из уравнения
определяется из уравнения
![]() .
.
Решая первое уравнение, находим функцию , то есть
![]() ,
,
Таблица 1

 y
y ,
, y
y
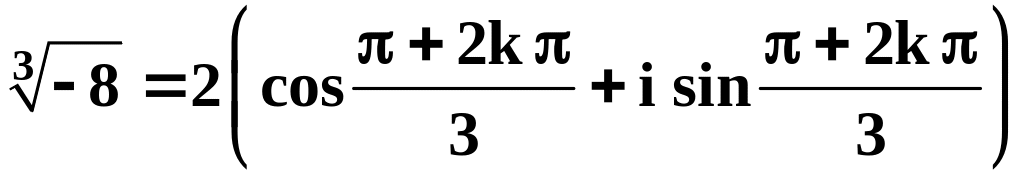 ,
,