7. Корреляционный анализ сигналов. Автокорреляционная и взаимно корреляционная функция.

Важнейшим понятием, расширяющим представление о сигналах и их свойствах, является корреляционный (или автокорреляционный) и взаимно-корреляционный анализ функций.

Корреляционная функция сигнала S(t) по определению равна 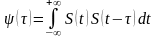(1.13)

где  временной сдвиг.

При нулевом сдвиге (=0) имеем (1.14)

где E – энергия сигнала. Следовательно, при нулевом временном сдвиге корреляционная функция равна энергии сигнала выделяющейся на единичном сопротивлении.

Основные свойства корреляционной функции ():

1. При =0 она положительна и имеет наибольшее значение, т. е. ;

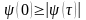2. Корреляционная функция является четной функцией сдвига, т. е. (–)=(), откуда следует, что .

Автокорреляционная функция вводится для количественного определения отличия сигнала S(t) и его смещенной во времени копии S(t–). Эта функция не дает представления о времени прихода сигнала.

Автокорреляционная функция прямоугольного импульса представлена на рис. 1.8.

Э нергия периодического сигнала равна , поэтому его энергетические свойства характеризуются отношением энергии за некоторый промежуток времени к длительности этого промежутка. Аналогично для корреляционной функции периодического сигнала 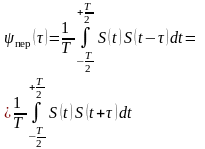(1.15)

где Т – период функции S(t). Можно показать, что автокорреляционная функция гармонического колебания есть также гармоническое колебание.

Кроме корреляционной функции можно также определить и взаимно-корреляционную функцию

.

(1.16)

Взаимно-корреляционная функция может не обладать свойствами четности или нечетности относительно .

Автокорреляционная функция и спектральная плотность связаны следующими соотношениями: 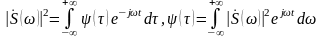, где 1 формула прямое а 2 формула обратное преобразование Фурье => прямое преобразование даёт спектральную плотность энергии, обратное – корреляционную функцию.

8. Классификация цепей. Основные свойства линейных цепей.

Элементы, из которых состоят все электрические цепи, можно разделить на пассивные и активные. Пассивными называют элементы электрической цепи, которые не могут увеличивать энергию действующего в цепи сигнала. К ним относятся сопротивления R, индуктивности L, емкости C. Активные же элементы могут увеличивать энергию сигнала.

Все элементы радиоэлектронных цепей, кроме того, подразделяются на элементы с сосредоточенными и распределенными параметрами. Если линейные размеры элементов намного меньше длины волны действующего в цепи сигнала, то они являются элементами с сосредоточенными параметрами. В противном случае мы имеем дело с элементами с распределенными параметрами.

В радиоэлектронных схемах преобразование сигналов осуществляется с помощью различных электрических цепей.

Электрические цепи можно разделить на два больших класса: линейные и нелинейные электрические цепи. Цепь называется линейной, если ее параметры не зависят от приложенного напряжения и протекающего в ней тока.

Очень часто какую-либо линейную или нелинейную электрическую цепь, составленную из пассивных и активных элементов, удобно рассматривать в виде четырёхполюсника, имеющего четыре доступных вывода. Два из них при этом образуют вход данной цепи, а два других – выход. К входным выводам может подключаться источник сигнала, а к выходным – нагрузка.

Основные свойства линейных цепей

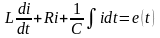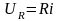С войство №1. Процессы в простых линейных цепях описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Приведем пример такой цепи. Если имеется простая последовательная цепь, состоящая из сосредоточенных пассивных элементов R, L, и C и источника эдс (рис. 2.1), то процессы в ней описываются уравнением , т. к. , и 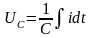или после дифференцирования имеем (2.1)

что соответствует указанному выше свойству.

Известно, что систему n уравнений первого порядка можно заменить одним уравнением n-го порядка. В силу этого, для более сложной цепи, состоящей из n простых цепей, справедливо уравнение:

,

(2.2)

где f(t) – некоторое внешнее воздействие.

Если все параметры a_n являются постоянными, то уравнение (2.2) описывает систему с постоянными параметрами.

Если хотя бы один из параметров a_n является функцией времени, то уравнение (2.2) будет характеризовать систему с переменными параметрами или параметрическую цепь.

Если параметры a_n являются функцией тока или напряжения, то мы будем иметь нелинейную систему.

Свойство линейности элементов можно истолковать как результат линейности их вольтамперных характеристик (=const).

Свойство №2. Для линейных цепей справедлив принцип независимости при наложении внешних воздействий (принцип суперпозиции). Этот принцип можно проиллюстрировать следующим образом. При действии на линейную систему нескольких внешних сил, поведение системы можно представить путем наложения (суперпозиции) решений, найденных для каждой из сил в отдельности. Для простоты рассмотрим цепь, которая при действии на нее силы f₁(t) описывается уравнением 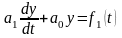(2.3)

Решением этого уравнения будет y₁(t), где y(t) может иметь значение тока, напряжения, заряда и.т. п.

При действии на эту же систему силой f₂(t), процессы будут описываться уравнением

.

(2.4)

Пусть его решением будет y₂(t)

При одновременном действии на систему сил f₁(t) и f₂(t) уравнение будет иметь вид

.

(2.5)

Решением его будет y₃(t). Если система линейна, то

y3(t)=y1(t)+y2(t)

(2.6)

Если же система нелинейна, то

y3(t)y1(t)+y2(t).

(2.7)

Свойство №3. В линейных системах не происходит преобразования спектра частот. Это свойство является следствием того, что операции интегрирования и дифференцирования являются линейными.

Так, для цепи на рис 2.1, воздействие f(t)=e(t) будет описываться тремя слагаемыми, линейно связанными протекающими по цепи токами с падениями напряжений на резисторе, индуктивности и ёмкости. Тогда , если, например, 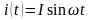, то , ,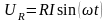

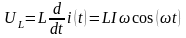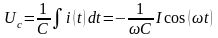
В случае сложного характера f(t), последняя разлагается на элементарные составляющие (в ряд Фурье) и на основании предыдущего принципа суперпозиции, каждая из составляющих даст решение с той же частотой.

В нелинейных цепях всегда происходит процесс преобразования спектра частот сигнала. Это же утверждение справедливо и для параметрических цепей, т. е. цепей с переменными параметрами a=a(t).

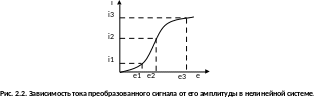
В нелинейной системе структура преобразованного сигнала зависит не только от времени но и от амплитуды. Если u₃=u₁+u₂, то i₃i₁+i₂.
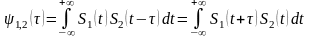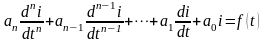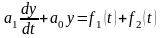