
- •Классификация сигналов и их параметры.
- •Периодические сигналы.
- •Спектральный состав последовательности прямоугольных импульсов при различном периоде их скважности.
- •Непериодические сигналы. Спектральная плотность.
- •Спектральная плотность прямоугольного импульса.
- •Импульсные сигналы. Основные параметры и характеристики.
- •Корреляционный анализ сигналов. Автокорреляционная и взаимно корреляционная функция.
- •Классификация цепей. Основные свойства линейных цепей.
- •Дифференцирующие цепи.
- •Интегрирующие цепи.
- •Четырехполюсники. Основные уравнения. Эквивалентные схемы.
- •Колебательные системы. Свободные колебания в одиночном контуре.
- •Последовательный колебательный контур. Резонанс напряжений.
- •Параллельный колебательный контур. Резонанс токов.
- •Связанные колебательные контуры. Резонансные кривые.
- •Электрические фильтры. Условие полосы прозрачности.
- •Простейшие rc-фильтры.
- •Усилительные элементы. Замена усилительного элемента эквивалентным генератором.
- •Температурная стабилизация усилительных элементов.
- •Основные показатели усилителей.
- •Предварительный усилитель. Принципиальная и эквивалентная схемы.
- •Усилитель напряжения низкой частоты. Работа усилителя в области низких, средних и верхних частот.
- •Основные свойства нелинейных цепей. Аппроксимация вах.
- •Воздействие гармонического сигнала на нелинейную цепь.
- •Воздействие бигармонического сигнала на нелинейную цепь.
- •Нелинейное резонансное усиление и умножение частоты.
- •Преобразование частоты сигнала.
- •Амплитудная модуляция.
- •Базовый модулятор.
- •Балансная модуляция.
- •Однополосная модуляция
- •Угловая модуляция.
- •Квадратичный режим детектирования ам-колебаний.
- •Линейный режим детектирования ам-колебаний.
- •Генерирование колебаний. Условия самовозбуждения колебаний.
- •Симметричный мультивибратор.
Преобразование частоты сигнала.
Для преобразования частоты в общем случае, очевидно, необходимо перемножить два колебания: основное (преобразуемого сигнала) и вспомогательное (гетородинное). Эту операцию можно осуществить различными способами с помощью нелинейных или параметрических цепей. Для этого, например, можно подать эти два напряжения на один и тот же электрод нелинейного элемента и выделить на выходе последнего составляющие суммарной или резонансной частоты – этот способ рассмотрен нами выше в разделе 4.4, посвященном анализу воздействия бигармонического сигнала на нелинейный элемент. Другой подход состоит в том, что преобразуемое колебание подается на элемент, коэффициент передачи или крутизна которого изменяется под воздействием гетеродинного напряжения, и из выходного колебания также выделяются составляющие суммарной или резонансной частоты.
Остановимся
подробнее на втором случае и покажем,
что изменяя крутизну элемента с частотой
гетеродинного напряжения, можно
осуществить преобразование частоты
сигнала. Положим, что крутизна этого
элемента является функцией времени и
изменяется с частотой гетеродинного
напряжения по закону
 (4.15)
(4.15)
При этом отметим, что выражение (4.15) не содержит членов, являющихся гармониками гетеродинного напряжения.
Подача
гармонического напряжения сигнала вида
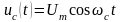 (4.16)
(4.16)
приводит к тому, что переменная составляющая выходного тока выразится как
|
|
(4.17) |
Формулу
(4.17) можно переписать в виде
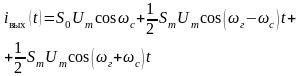 (4.18)
(4.18)
Если
колебательный контур, включенный на
выходе преобразователя настроен на
резонансную частоту, равную промежуточной
частоте fп,
 (4.19)
(4.19)
Или
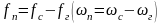 (4.20)
(4.20)
то напряжение на этом контуре будет пропорционально току, равному слагаемому с разностной частотой г–с.
Для
оценки эффективности работы преобразователя
вводят количественную характеристику
– крутизну преобразования Sпр,
равную отношению амплитуды тока
промежуточной частоты к амплитуде
напряжения сигнала. Таким образом
 (4.21)
(4.21)
Из
выражения (4.18) следует, что
 (4.22)
(4.22)
т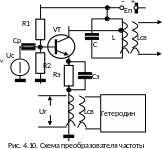 . е.
крутизна преобразования равна половине
амплитуды дифференциальной крутизны
параметрического элемента.
. е.
крутизна преобразования равна половине
амплитуды дифференциальной крутизны
параметрического элемента.
На рис.4.10 приведена схема простого транзисторного преобразователя частоты. Транзистор VT включен по схеме с общим эмиттером (ОЭ). Напряжение Uг гетеродина вводится в цепь эмиттера, в результате чего периодически с частотой гетеродина fг меняется крутизна S(t) транзистора. Входной сигнал Uc подается в цепь базы. Выходной колебательный контур с частичным включением настроен на частоту fп.
Амплитудная модуляция.
Для выяснения
основных особенностей АМ рассмотрим
модуляцию несущего гармонического
колебания с частотой 0,
изменяющегося по закону
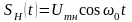 (4.24)
(4.24)
простым гармоническим
сигналом с частотой
(рис. 4.11 а, б)
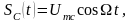 (4.25), положив для простоты начальную
фазу обоих сигналов равной 0. В этом
случае амплитуду несущих модулированных
колебаний
(4.25), положив для простоты начальную
фазу обоих сигналов равной 0. В этом
случае амплитуду несущих модулированных
колебаний
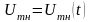 ,
очевидно, можно представить в вид
,
очевидно, можно представить в вид
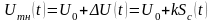 (4.26),
где
U0=const,
а U(t)=kSc(t)
– приращение амплитуды, прямо
пропорциональное величине напряжения
сигнала сообщения, изменяющегося в
соответствии с формулой (4.25). Здесь k
– коэффициент пропорциональности.
Подставив соотношение (4.25) в выражение
(4.26), получим
(4.26),
где
U0=const,
а U(t)=kSc(t)
– приращение амплитуды, прямо
пропорциональное величине напряжения
сигнала сообщения, изменяющегося в
соответствии с формулой (4.25). Здесь k
– коэффициент пропорциональности.
Подставив соотношение (4.25) в выражение
(4.26), получим
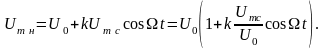 (4.27). Обозначив
коэффициент kUm c/U0
при
(4.27). Обозначив
коэффициент kUm c/U0
при
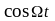 через m,
выражение (4.27) можно переписать в виде
через m,
выражение (4.27) можно переписать в виде
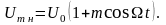 (4.28)
(4.28)
Подставив выражение
(4.28) в соотношение (4.24), получим
SAM(t) (4.29)
(4.29)
Выражение
(4.29) показывает, что при АМ амплитуда
высокочастотного колебания изменяется
по закону модулирующего сигнала
(риc.4.11 в).
Величина m
называется коэффициентом модуляции
или глубиной модуляции. Учитывая, что
0
cost
1, коэффициент
m
может быть выражен через наибольшее и
наименьшее значения амплитуды
модулированных колебаний Umн макс
и Umн мин
следующим образом
 (4.30)
(4.30)
Измерение коэффициента глубины модуляции, изменяющегося в соответствии с выражением (4.30), удобно проводить с помощью осциллографа по двойной амплитуде А и В (рис. 4.11 в). Тогда
|
|
(4.31) |
Х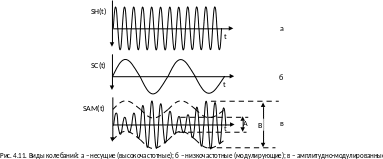 арактерная
величина коэффициента глубины модуляции
m
на практике составляет в среднем (30
80) %. Анализ АМ сигналов и наладку
радиоприемной аппаратуры обычно проводят
при величине m=30%.
АМ сигналы получают с использованием
нелинейного элемента, которым может
являться, в частности, транзистор. В
этом случае применяют базовую или
эмиттерную модуляцию. Проанализируем
работу схемы базовой модуляции на
биполярном транзисторе, представленную
на рис. 4.12.
арактерная
величина коэффициента глубины модуляции
m
на практике составляет в среднем (30
80) %. Анализ АМ сигналов и наладку
радиоприемной аппаратуры обычно проводят
при величине m=30%.
АМ сигналы получают с использованием
нелинейного элемента, которым может
являться, в частности, транзистор. В
этом случае применяют базовую или
эмиттерную модуляцию. Проанализируем
работу схемы базовой модуляции на
биполярном транзисторе, представленную
на рис. 4.12.

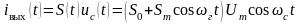 .
.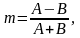 0<m<1
или
0<m<1
или
