Приближенное решение систем уравнений.

§25. Приближенное решение систем линейных уравнений.

Рассмотрим сущность итерационного метода при решении систем линейных уравнений на примере. Пусть дана система Ax=B, где А=(а_ij) - матрица коэффициентов при переменных х_ij размерности n´n, x=(x₁, x₂, …, x_n) - матрица переменных, 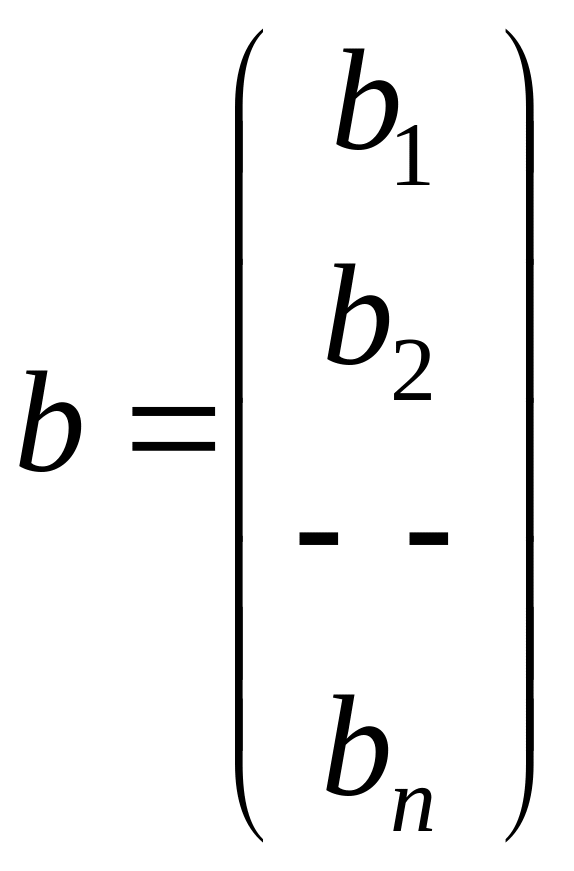- матрица свободных членов. Она может быть преобразована к эквивалентной ей системе вида x=Bx+c, где В и с - некоторые новые матрица и свободный член соответственно. Данную систему можно трактовать как задачу о неподвижной точке линейного отображения В в пространстве R_n и определить последовательность приближений х^(k) к неподвижной точке х^* рекуррентным равенством x^(k+1)=Bx^(k)+c, k=0, 1, 2, … . Итерационный процесс, начинающийся с некоторого значения называется методом простых итераций.

Пусть исходная линейная система уравнений имеет вид:

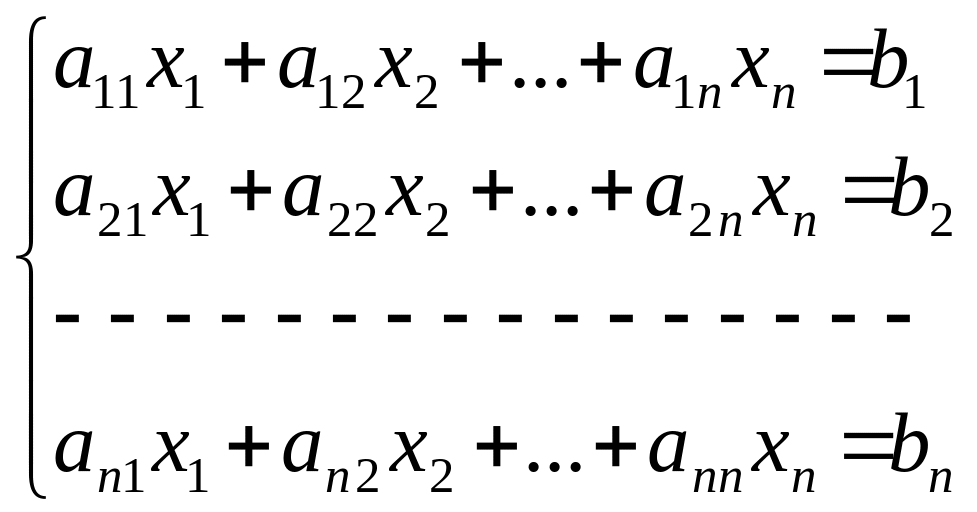
(1)

При решении этой системы необходимо:

I. Задать начальное приближенное решение (индекс в скобках указывает номер итерации), которое будет уточняться в процессе итераций. При этом надо учитывать, что, если метод сходится, то он сходится при любом начальном приближении. Обычно в качестве начального приближения, в зависимости от задачи, берутся либо вектор правых частей и тогда , либо нулевой вектор и тогда .

II. Привести исходную систему (1) к виду, удобному для проведения итераций, то есть к виду

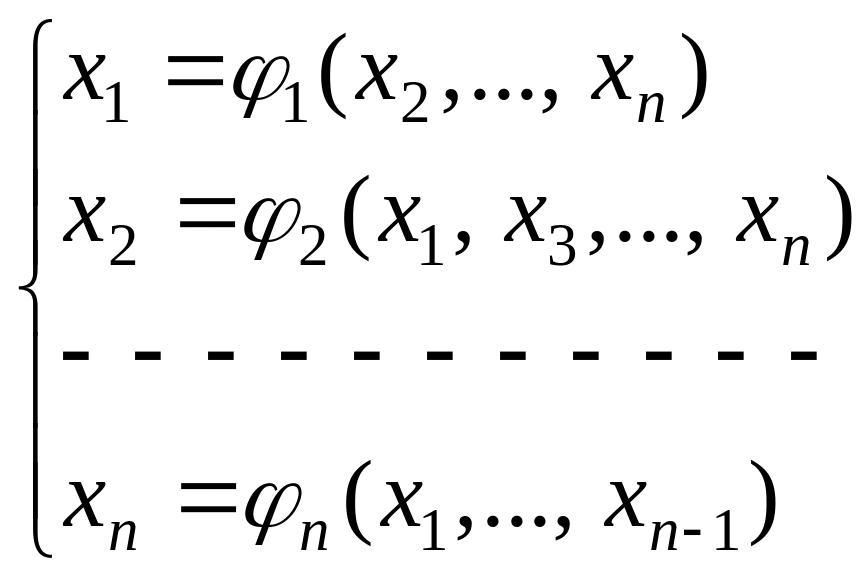(2)

где - произвольные линейные функции переменных , причем некоторые переменные могут отсутствовать в правых частях системы (2), но каждая переменная должна присутствовать в левой части соответствующего уравнения.

III. Указать совокупность действий, которые составляют одну итерацию (переход от к ). Достаточно рассмотреть два алгоритма вычисления корней уравнений системы.

1. Метод простой итерации записывается в виде:

Первая итерация выглядит следующим образом:

;

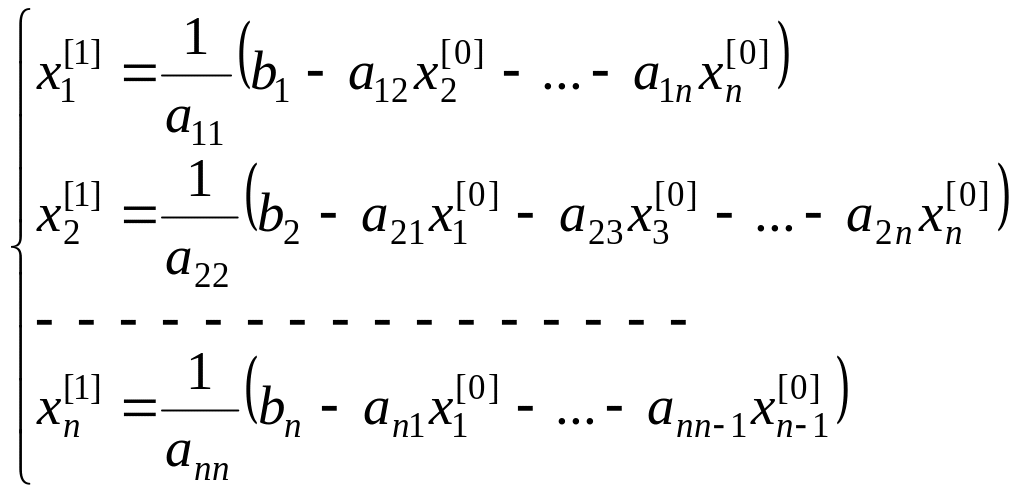Затем, на каждом следующем шаге значение верхних индексов увеличивается на единицу. В итоге, на последнем шаге система имеет вид:

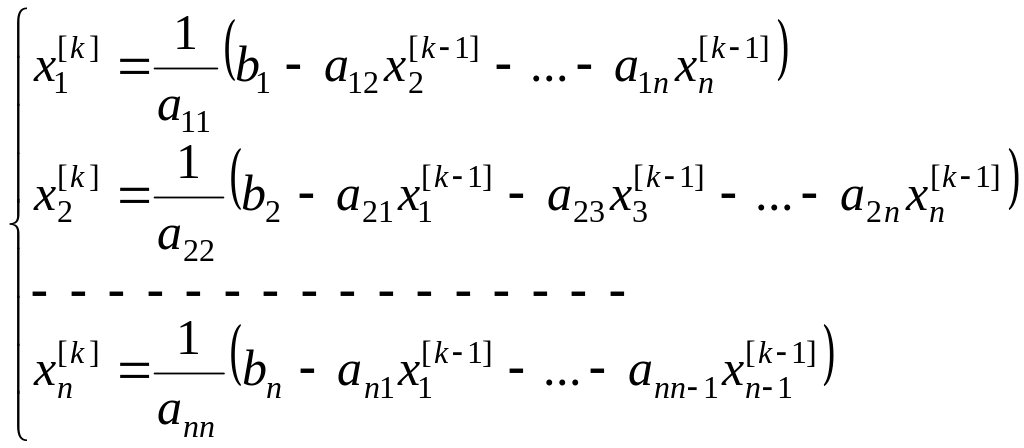. (3)

2. Метод Зейделя (обобщение метода простой итерации) заключается в следующем: уже полученные значения переменных используются при вычислении остальных искомых переменных на этой итерации. То есть имеет место:

;

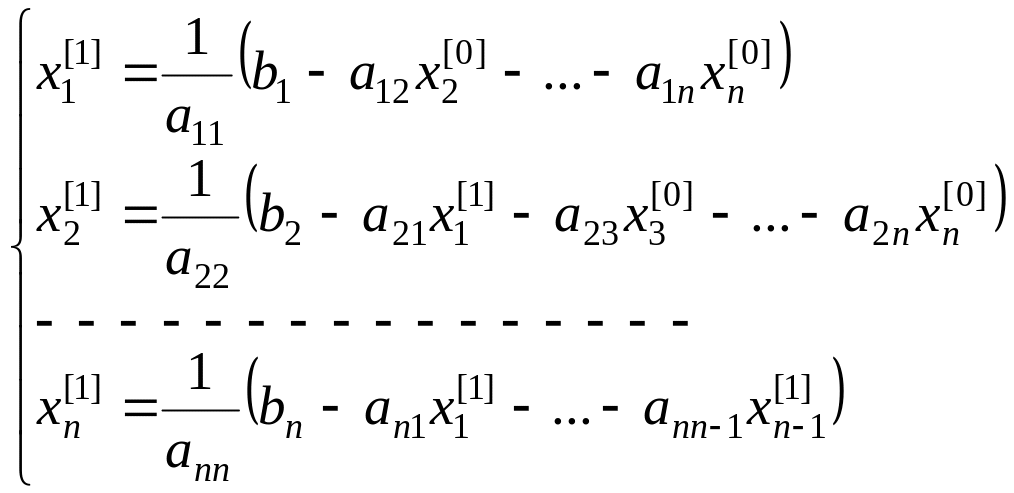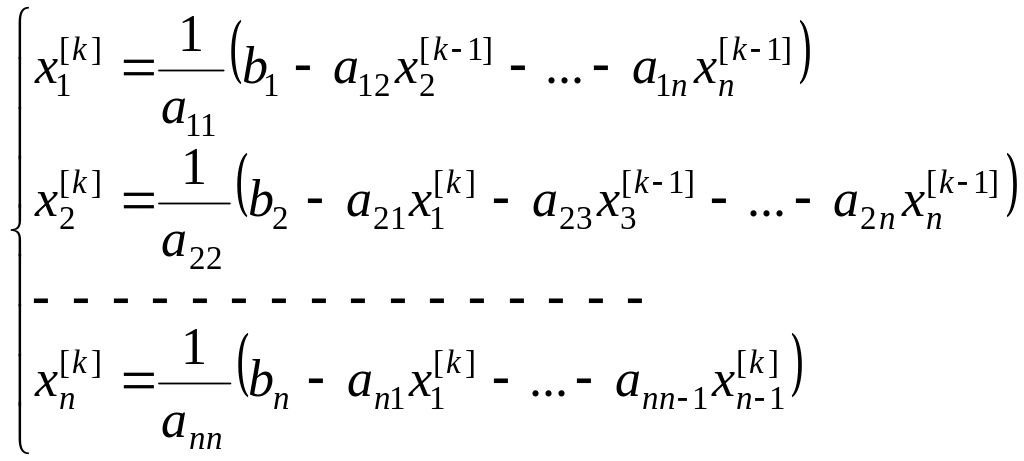_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ . (4)

Применяя каждый из методов, необходимо учитывать, что метод Зейделя сходится на порядок быстрее метода простой итерации.

IV. Выяснить условия сходимости итерационного процесса. При решении практических задач используется следующая теорема: Если матрица А исходной системы имеет диагональное преобладание, то методы простой итерации и Зейделя сходятся.

Определение. Матрица А=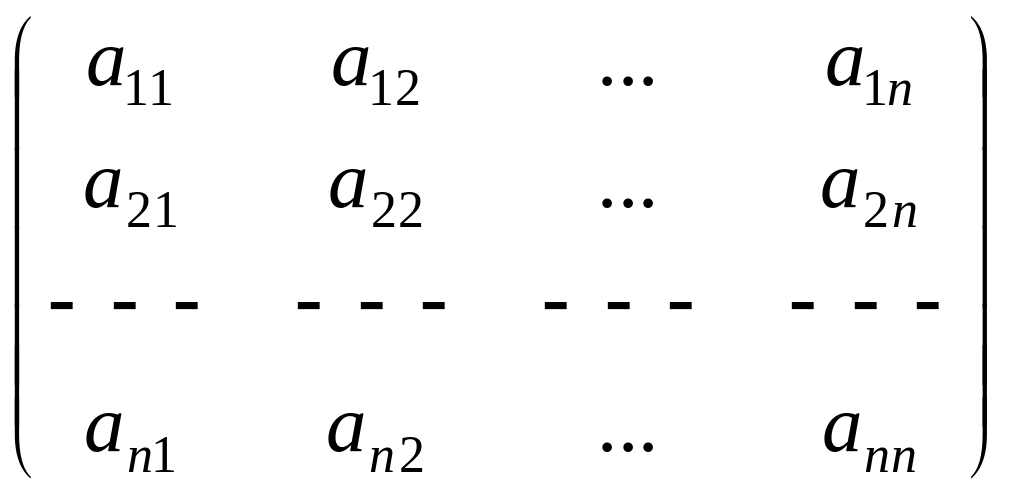 исходной системы называется имеющей диагональное преобладание, если выполняются следующие условия:

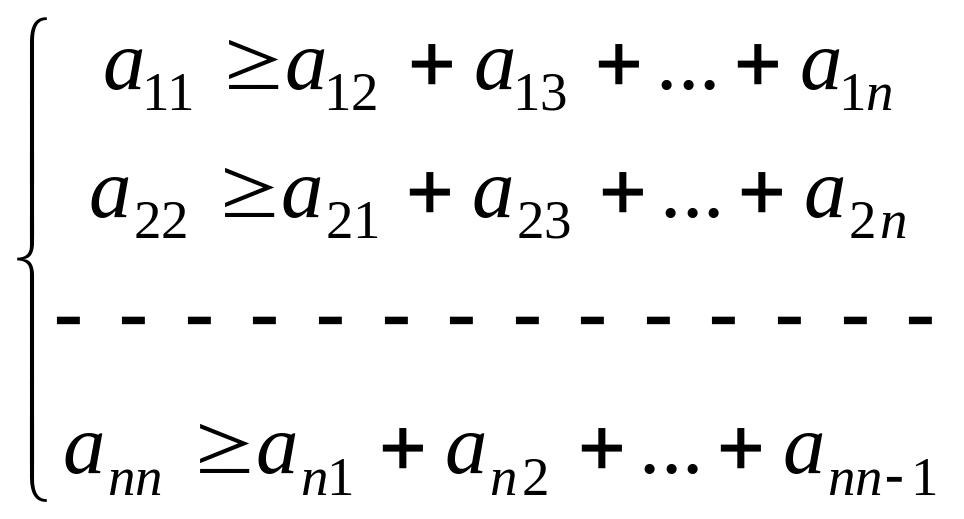
V. Указать условия окончания итерационного процесса. В этой роли обычно выступает оценка , где ε - наперед заданная точность вычислений.

§26. Приближенные методы решения систем нелинейных уравнений.

Многие практические задачи при их математическом моделировании сводятся к решению системы нелинейных уравнений. Система n нелинейных уравнений с n неизвестными в общем случае имеет вид

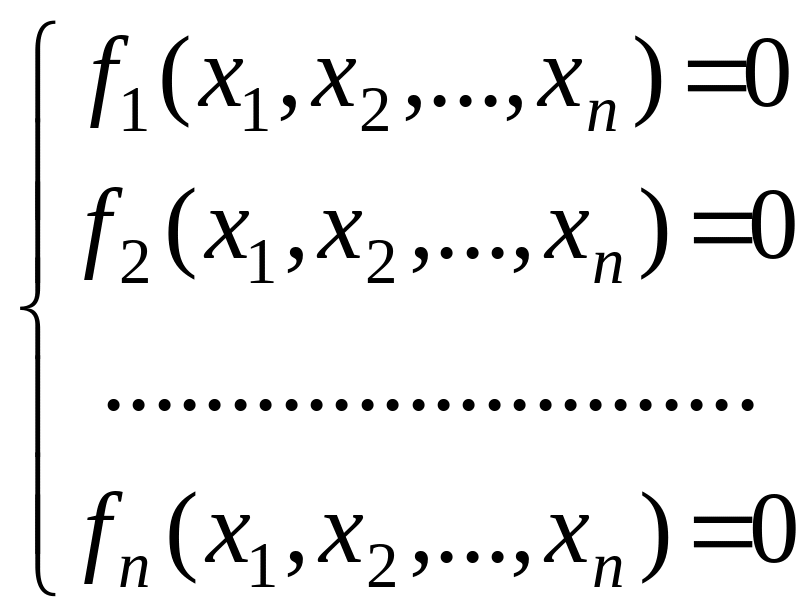(1)

Решением системы уравнений (1) называется n чисел которые при подстановке в (1) обращают все уравнения в нули.

Задача (1) тесно связана с другой очень часто встречающейся задачей - минимизации функции многих переменных

(2)

Эта связь проявляется в том, что каждую из этих задач можно свести к решению другой. Пусть, например, вектор является решением системы (1). Построим функцию

(3)

Так как обращает в нуль все уравнения системы (1), то обращает функцию в нуль. Поскольку , то обращает функцию Q в минимум, и этот минимум равен нулю. Справедливо и обратное утверждение. Пусть совокупность чисел обращает функцию в минимум, равный нулю. Тогда каждый член суммы, входящий в (3), обращается в нуль и, следовательно, совокупность является решением системы (1). Таким образом, задача (1) сводится к нахождению минимума (3).

В свою очередь, для задачи минимизации (2) точка минимума является решением системы нелинейных уравнений.

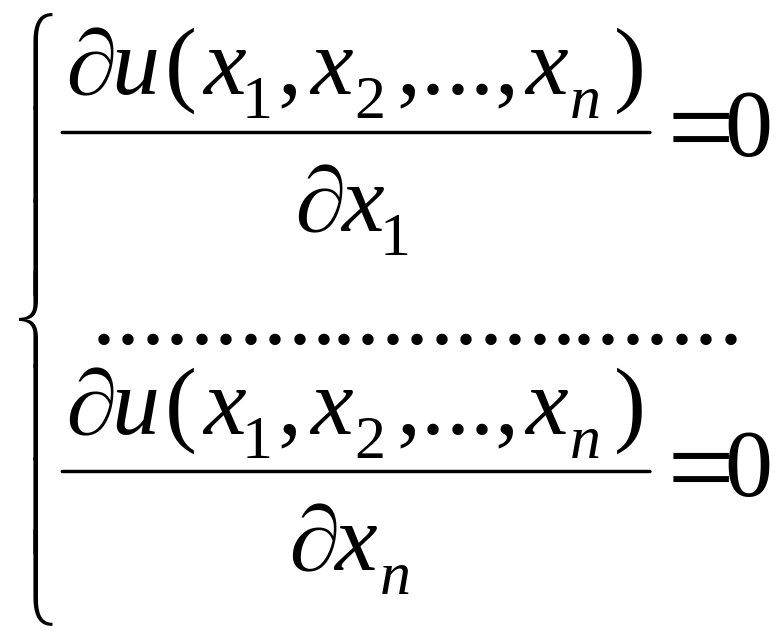
Возможность сведения одной задачи к другой не означает, что можно ограничиться рассмотрением только одной из них. Каждая из них является весьма сложной и имеет многочисленные подводные камни, которые проявляются при практической реализации существующих методов их решения. По-видимому, не существует никаких универсальных методов решения этих задач. Установление связи между задачами (1) и (2) удобно тем, что в каждом конкретном случае мы можем использовать ту из них, которая быстрее приводит к цели при располагаемых ресурсах вычислительной техники и математического обеспечения. Трудности при решении систем нелинейных уравнений проявляются в следующем:

1. Определение количества корней системы и их отделение проводить достаточно сложно в силу невозможности при больших n использовать простые геометрические соображения.

2. Многие надёжные методы нахождения корня одного нелинейного уравнения, имеющие гарантированную сходимость, такие как метод половинного деления или метод хорд и т. д., не допускают обобщения на случай n неизвестных.

3. Решение системы (1) ищут, как правило, методом итераций или эффективным по скорости методом Ньютона, сходимость которых возможна только при наличии хорошего начального приближения.

4. нахождение хорошего начального приближения для сложной системы (1) является весьма непростым делом и требует, помимо математического анализа системы, привлечение других соображений (физических, инженерных, экономических и др.), связанных с постановкой решаемых задач.

Замечание 1. никаких универсальных методов преодоления отмеченных трудностей и решения этих задач не существует. Каждый раз приходится, наряду с теоретическими исследованиями системы (1), использовать эвристические соображения и проводить экспериментальные численные исследования. Рассмотрим названные в пункте 3 методы.