§4. Фундаментальная система решений системы линейных однородных уравнений. Ядро линейного оператора и его базис.

Рассмотрим систему линейных однородных уравнений с неизвестными ранга .

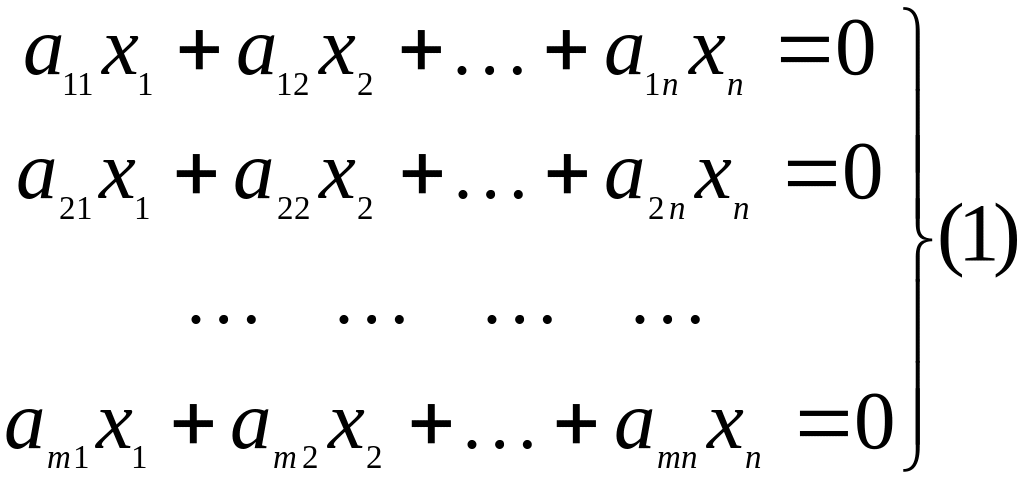
Теорема. Множество решений системы (1) является подпространством -мерного арифметического пространства R_n.

Для доказательства теоремы достаточно проверить два свойства:

1. Если и два решения системы (1), то их сумма

также решение этой системы. Для этого подставим этот набор чисел в i-тое уравнение системы (1), где i=l,m, получим:

Значит, является решением системы уравнений (1).

2. Докажем, что произведение любого решения системы (1) на любое число также является решением той же системы уравнений.

Подставим набор чисел в левую часть i-того ур-ния системы (1):

Значит,

является решением системы уравнений (1). Таким образом, мы доказали, что множество решений системы (1) - подпространство R_n.

Опр. Базис подпространства решений системы линейных однородных уравнений называется фундаментальной (базисной) системой решений (ФСР).

Как следует из определения базиса, фундаментальная система решений обладает двумя свойствами: решения, составляющие ФСР, линейно независимы, любое решение системы есть линейная комбинация фундаментальной системы решений. Теорема (о ФСР). Если ранг системы линейных однородных уравнений с неизвестными равен , то ФСР состоит из решений.

Опр. Множество векторов линейного пространства, переходящих в нулевой вектор под действием линейного оператора , называется ядром оператора и обозначается как ker .

Теорема. Ядро оператора является подпространством линейного пространства, в котором задан линейный оператор .

Доказательство. Пусть , тогда и . Сложим эти равенства, получим , так как линейный оператор, то в силу линейности , получим , откуда следует, что . Аналогично, из следует, что . В силу линейности , отсюда . Значит, ker - подпространство. Ч.т.д.

Рассмотрим в линейном пространстве базис и оператор , который задается в данном базисе матрицей

А=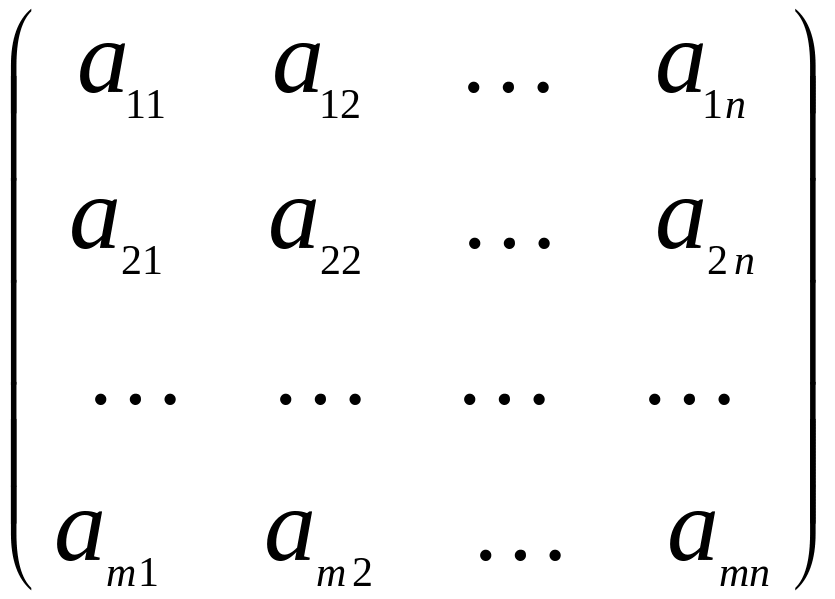

Тогда ядро оператора задается уравнением

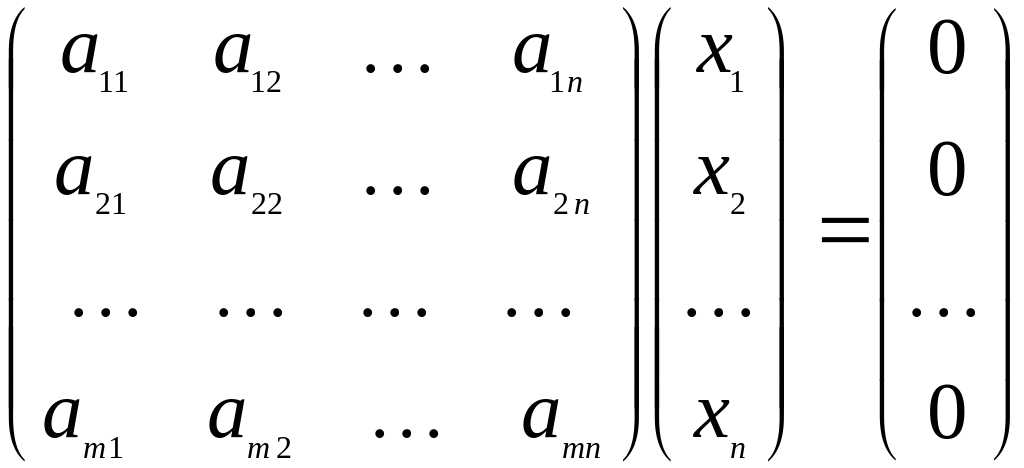или системой уравнений:

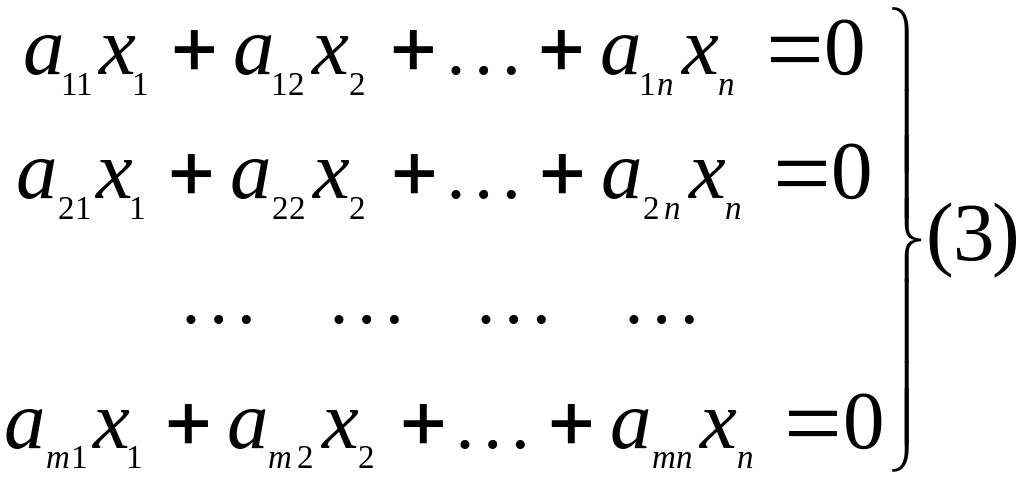
Фундаментальные решения системы (3) задают базисы ядра оператора , заданого матрицей А.

5(1). Полож. Опред. Квадратичные формы.

Квадратичной формой от неизвестных называется сумма вида где .

Опр.2. Квадратичная форма называется положительно определенной, если она принимает только положительные значения для любых ненулевых векторов.

Лемма. Знак определителя матрицы квадратичной формы не зависит от выбора базиса.

Теорема. Квадратичная форма является положительно определенной тогда и только тогда, когда ее нормальный вид , то есть если и ранг, и положительный индекс инерции равны числу неизвестных.

Зам. Решить вопрос о том, является ли данная квадратичная форма положительно определенной, возможно и без приведения формы к нормальному виду. Это позволяет сделать критерий Сильвестра. Чтобы понять формулировку этого критерия, нам потребуется

Опр. Пусть — матрица квадратичной формы. Обозначим через минор матрицы А, элементы которого расположены в ее первых k строках и первых k столбцах. Другими словами,

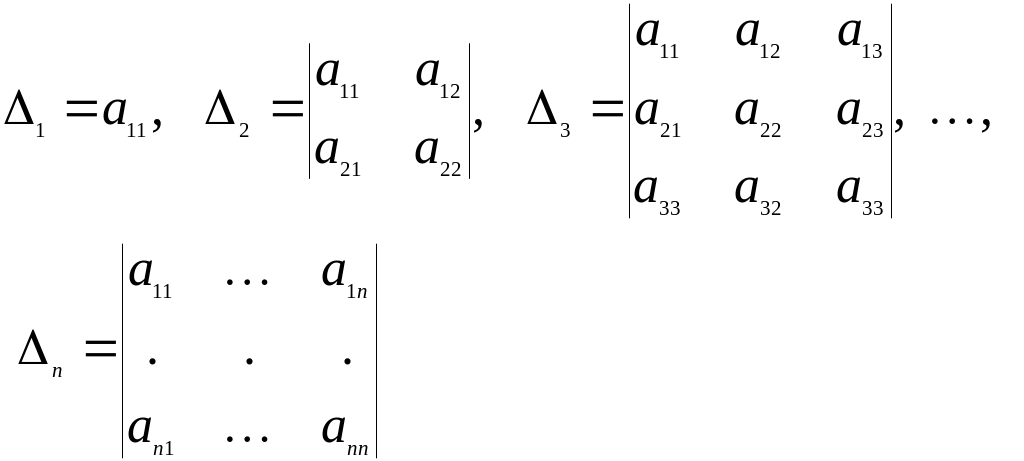
Будем называть эти миноры главными минорами квадратичной формы.

Теорема (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все ее главные миноры строго положительны.

Проведем методом математической индукции по числу переменных. База индукции:

. Очевидно, что эта квадратичная форма будет положительно определенной тогда и только тогда, когда .

Шаг индукции: Предположим, что квадратичная форма от переменных является положительно определенной, тогда и только тогда, когда все ее главные миноры строго положительные.

Докажем, что это утверждение справедливо и для квадратичной формы от переменных.

Пусть теперь дана квадратичная форма от переменных .

В квадратичной форме соберем все члены, не содержащие переменного , тогда, очевидно, мы получим квадратичную форму f от -переменных. Тогда можно записать в виде

(1)

Покажем, что если является положительно определенной, то также положительно определена. Докажем это методом от противного. Предположим, что - положительно определена, не является положительно определенной. Значит, существуют такие значения переменных, , среди которых не все равны нулю, при которых.

. Полагая дополнительно , подставим в (1). Получим , что невозможно, так как положительно определена. Значит, если положительно определена, значит, также является положительно определенной. Кроме того, очевидно, что главные миноры квадратичной формы являются одновременно главными минорами квадратичной формы .

Необходимость. Пусть является положительно определенной. Докажем, что все главные миноры строго положительны.

Так как положительно определена, значит по доказанному раннее также положительна. Тогда по допущению все главные миноры положительны. Осталось доказать, что

Всякую положительную квадратичную форму с помощью невырожденного линейного преобразования можно привести к нормальному виду с матрицей , определитель которой равен 1 > 0

По лемме, знак определителя матрицы квадратичной формы не меняется. Значит, .

Достаточность. Пусть строго положительны все главные миноры квадратичной формы . Докажем, что является положительно определенной.

Так как положительны, то по индуктивному предположению является положительно определенной. Следовательно, существует невырожденное линейное преобразование переменных , которое приводит форму

к виду .

Это линейное преобразование можно дополнить до невырожденного линейного преобразования всех неизвестных , полагая х_п =у_п.

Тогда форма приводится указанным преобразованием к виду

(3)

Дополним члены, содержащие до полных квадратов:

или

где

Рассмотрим следующее невырожденное линейное преобразование

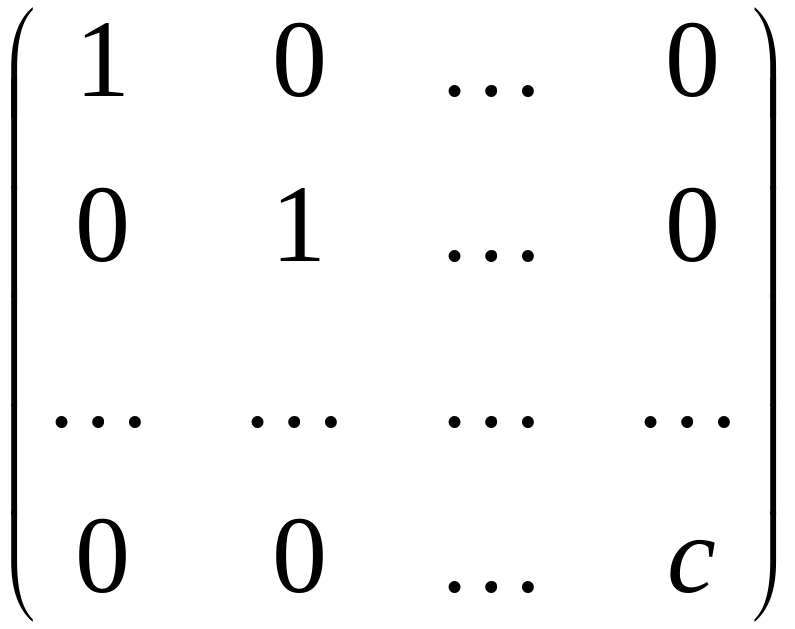которое приводит форму к виду с матрицей , детерминант этой матрицы равен с.

По лемме, знак определителя матрицы квадратичной формы не меняется, так как (по условию), то

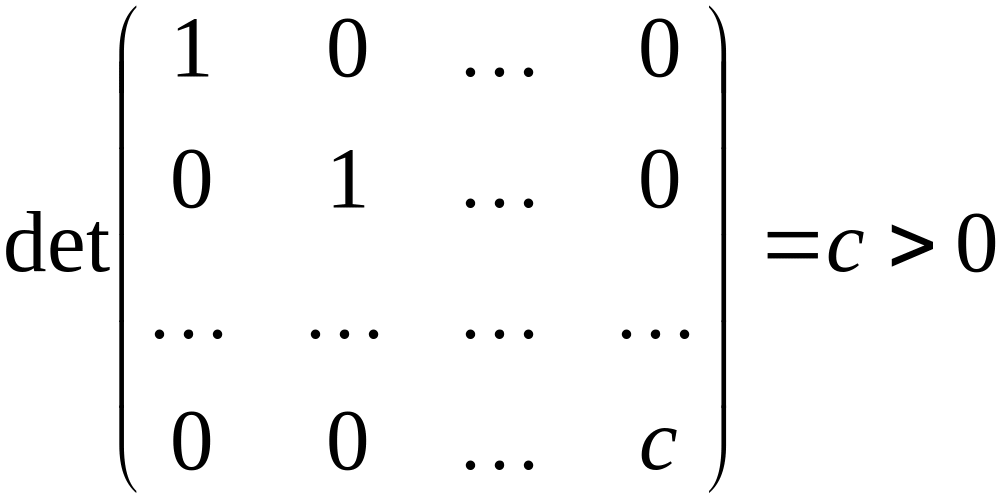
Значит, является положительно определенной.