2.2.3 Постановка задачи расчета сложного сопряженного теплообмена

Для расчета сложного теплообмена в печи №6 ООО «ТСМ Тяжмаш» решалось уравнение энергии, записанное в терминах температуры:

(2.23)

здесь с_p — удельная изобарная теплоемкость, Дж/(кг·К); λ_эфф — эффективный коэффициент теплопроводности, Вт/(м·К); T — абсолютная температура, К; S_r — источниковое слагаемое, возникающее в результате учета радиационной составляющей теплообмена, Вт/м³.

Зависимости плотности от температуры в соответствии с уравнением Гей-Люссака имеет следующий вид:

,

(2.24)

где — плотность дымовых газов при нормальных условиях, кг/м³; T — абсолютная температура, К.

Уравнение переноса излучения в нерассеивающей среде:

(2.25)

где — коэффициент «радиационной» теплопроводности, Вт/(м·К); T — абсолютная температура, найденная из уравнения (2.23), К; T_r — «радиационная» температура, К; a — коэффициент поглощения газовой среды, м^-1, σ₀ — постоянная Стефана-Больцмана, равная 5,67·10^-8 Вт·м^-2·К^-4.

Расстояние между ближайшими твердыми поверхностями, которое фигурирует в коэффициенте (2.6), рассчитывается после решения уравнения (2.12) по найденному локальному значению скалярной величины W и ее градиенту из соотношения:

.

(2.26)

Источниковое слагаемое в уравнении (2.23) вычисляется следующим образом:

.

(2.27)

Начальные условия при расчете сложного теплообмена следующие:

• температура нагреваемых роликов:

  0С;

  (2.28)

• температура дымовых газов внутри печного пространства:

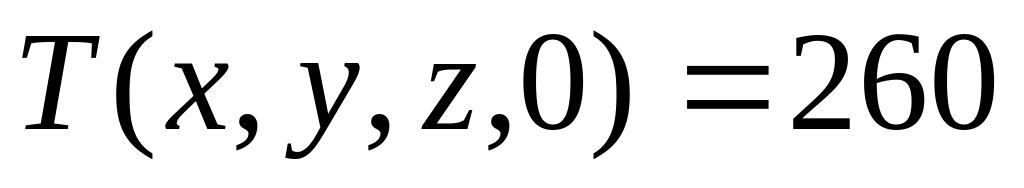  0С;

  (2.29)

• «радиационная» температура газа в рабочем пространстве печи:

  0С;

  (2.30)

• температура футеровки и выкатного пода, соответственно:

0С,

(2.31)

и

0С.

(2.32)

Граничные условия:

• для уравнения энергии (см. уравнение (2.23)) в приграничной к соплу горелочного устройства контрольном объеме задавались объемные тепловыделения от горения топлива, которые находились следующим образом:

,

(2.33)

,

(2.34)

где — объемные тепловыделения, Вт/м³; Q — поток тепла, Вт; , — удельные объемные теплоемкости воздуха и топлива соответственно, Дж/(м³·К); , — объемные расходы воздуха и топлива при нормальных условиях соответственно, нм³/с; , — температуры подогрева топлива и воздуха соответственно, равные 293 К; — низшая рабочая теплота сгорания топлива, равная 35170 кДж/м³; — величина контрольного объема, в котором происходят тепловыделения, м³.

• плотность теплового потока, теряемого в окружающую среду, на внешних стенках и своде печи рассчитывается по формуле конвективной теплоотдачи:

(2.35)

здесь T_w — температура на стенке печи, К; T₀ — температура окружающей среды (принята равной 293 К); α — коэффициент конвективной теплоотдачи (принят равным 12 Вт/(м²·K)).

В таблице 2.3 сведены значения потоков тепла в результате тепловыделений.

Теплофизические и радиационные свойства стали, огнеупорных и теплоизоляционных материалов, а также газов почерпнуты из справочной литературы /174-176/.

Таблица 2.3

Поток тепла в результате тепловыделений

Интервал времени, ч.	Поток тепла через одну горелку, Вт	Тепловыделения в печи, Вт
00,5	42891,84	514702,08
0,51	56436,63	677239,58
11,5	70365,19	844382,31
1,52	84677,52	1016130,3
22,5	99147,88	1189774,5
2,53	113776,3	1365315
33,5	127591,9	1531103,3
3,54	140594,9	1687139,3
44,5	153394,8	1840737,2
4,55	165991,4	1991897,1
55,5	154410,6	1852927,5
5,56	118652,4	1423828,5
Продолжение таблицы 2.3
66,5	93052,72	1116632,6
6,57	77611,66	931339,88
77,5	67859,41	814312,88
7,58	63795,97	765551,63

Решение поставленной задачи производилось методом «контрольного объема» Сполдинга–Патанкара /26/ на адаптивной сетке, показанной на рис. 2.3 и 2.4, с суммарным количество узлов — 168 432. Ось Z направлена вверх, X — вдоль, а Y — по ширине печи. Шаг по времени задавался равным 30 минутам. Вычислительная процедура реализовывалась с помощью вычислительного комплекса PHOENICS /168/, версии 3.6.0 на персональном компьютере.

Основные особенности решения дифференциальных уравнений переноса описаны в Приложении 1.

Характерные особенности решения данной задачи следующие:

• для замыкания системы уравнений Навье–Стокса использовалась k-l–модель турбулентности. При этом длина пути смешения рассчитывалась с учетом расстояния до ближайшей твердой поверхности;

• для аппроксимации конвективных членов уравнений (2.8)-(2.10), (2.23) использовалась комбинированная схема;

• для численного согласования решений осредненных уравнений неразрывности и Навье–Стокса использовался алгоритм SIMPLEST;

• сложный теплообмен моделировался путем решения уравнения энергии, в котором вклад РТО учитывался в источниковом слагаемом;

• лучистый теплообмен рассчитывался с помощью модели Immersol, особенностью которой является использование уравнения «радиационной теплопроводности» для описания процесса РТО. В рамках данного подхода, как и для расчета пути длины смешения, используется уравнение (2.12) для определения расстояния между ближайшими излучающими поверхностями.

Рис. 2.3 Адаптивная сетка в сечении YZ (66×44 узла).

Рис. 2.4 Адаптивная сетка в сечении XZ (58×44 узла).