56 Электромагнитный момент ад.

Напряжение для электромагнитного момента может быть получено через электромагнитные силы и через электромагнитную мощность.

В первом случае для АД с фазным ротором:

; (1)

;

,

где обмоточный коэффициент обмотки ротора ;

количество проводников обмотки ротора ;

число пар полюсов обмотки ротора ;

действующее значение магнитной индукции в зазоре между статором и ротором ;

полюсное деление ;

диаметр ротора ;

активная длина проводников.

Обмоточный коэффициент обмотки ротора равен:

;

;

,

где коэффициент укорочения первой гармоники ;

коэффициент распределения обмотки ротора ;

угол укорочения обмотки ;

геометрическая сумма ЭДС катушечной группы ;

ЭДС катушки ;

число катушек обмотки.

Для АД с короткозамкнутым ротором:

. (2)

Электромагнитная мощность равна:

. (3)

Из схемы замещения (Г-образной) найдём приведённый ток на ротора:

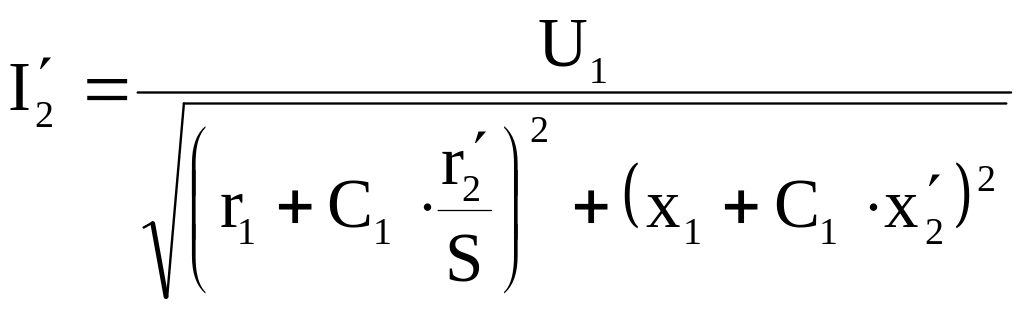. (4)

Разделим уравнение (3) на

и заменяя ток его значением из (4), получим:

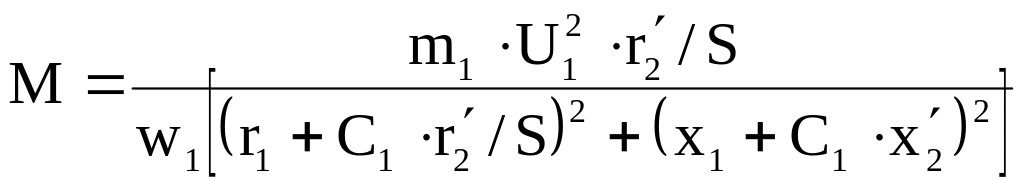. (5)

При электромагнитный момент зависит только от сколь-жения S. Зависимость M=f(S) называется механической характеристикой АД. При малых значениях электромагнитный момент будет равен:

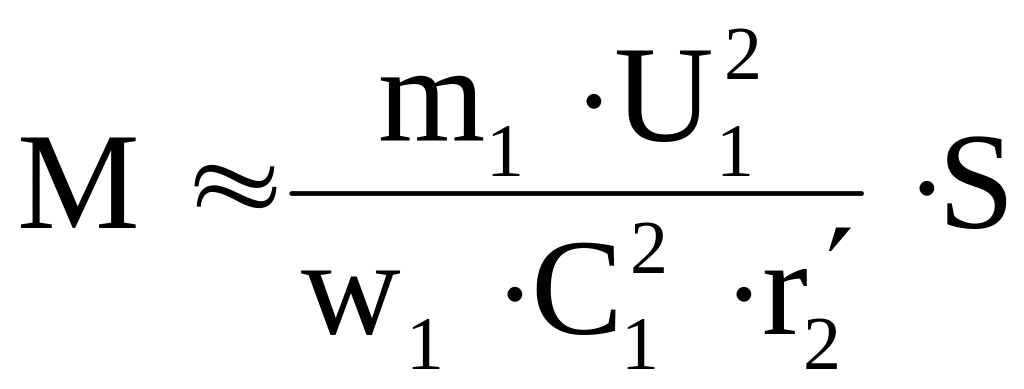, (6)

то есть при малых значениях S имеет место линейная зависимость M=f(S).

При S близких к единице можно пренебречь активными сопротив-лениями обмоток статора и ротора , так как они малы по сравнению с их индуктивными сопротивлениями. Тогда можно записать:

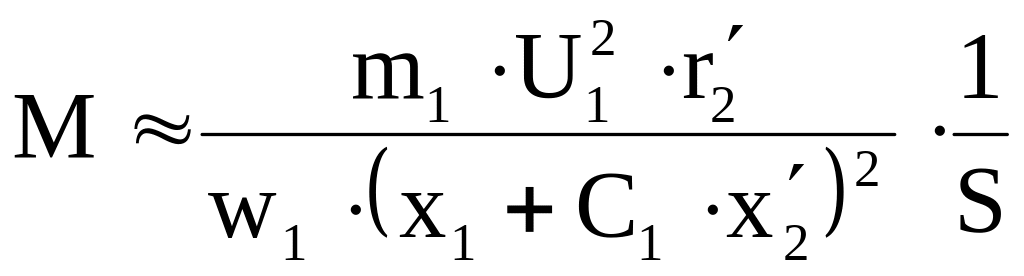, (7)

то есть при S близких к единице имеет место обратная зависимость M=f(x).

57 Механическая характеристика ад.

График соответствующий уравнению:

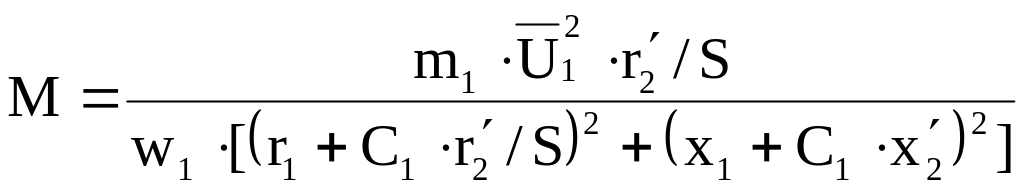, (1)

имеет следующий вид .

На графике можно выделить три возможных режима работы : генера-торный ; двигательный и тормозной .

Нормальная работа двигателя обычно протекает на линейном участке. Здесь находится точка номинального режима работы. Номинальный момент соответствует номинальному скольжению Максимальный момент соответствует критическому скольжению Кратность максимального момента к номинальному . Более высокие значения соответствуют АД с меньшим числом полюсов.

Момент при скольжении S=1 называется пусковым . Кратность пускового момента к номинальному

Механическую характеристику можно представить в виде зависимости . Для этого в уравнении (1) заменяется на . Для получения выражения для необходимо уравнение (1) продифференцировать по S и приравнять нулю, то есть . В результате получим:

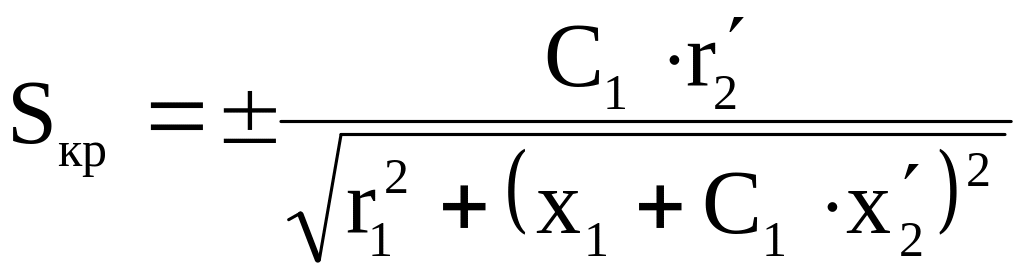. (2)

Подставив в (1), получим:

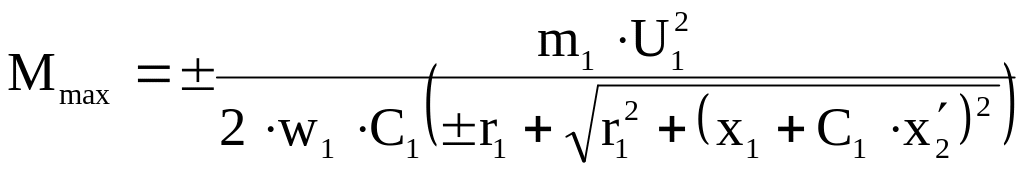. (3)

58 Устойчивость работы ад.

Исполнительный механизм приводится в движение посредством двигателя. Установившийся режим работы агрегата наступает при такой скорости (скольжения) двигателя, при которой его электромагнитный момент уравновешивает момент статического сопротивления:

(1)

где М₂ – тормозной момент ИМ, М₀ – тормозной момент, обусловленный механическими и магнитными потерями внутри двигателя.

В установившемся режиме во времени. Если равенство нарушается, то происходит изменение скорости в соответствии с известным из механики уравнением движения:

(2)

где - динамический момент.

Из уравнения (2) следует:

1) при и

Т.к. положительному приращению времени будет соответствовать положительное приращение скорости , то в этом случае будет происходить разгон двигателя и ИМ;

2) при и

Здесь положительному приращению времени соответствует отрицательное приращение скорости . В этом случае будет происходить замедление агрегата.

Скорость, соответствующую установившемуся режиму, графически можно определить по точке пересечения механических характеристик и или и . Точки, соответствующие установившимся значениям скорости или скольжения, могут соответствовать устойчивому или неустойчивому равновесию.

Равновесие будет устойчивым, если после прекращения кратковременных возмущений, выводящих систему из равновесия, она вновь возвращается в исходную точку. В противном случае равновесие будет неустойчивым.

На рисунке точка при скольжении является точкой неустойчивого равновесия. Точки со скольжением и являются точками устойчивого равновесия.

В общем случае критерием устойчивости является выполнение неравенств:

или (3)

Необходимо, чтобы равновесие было на линейном участке.