54 Векторная диаграмма ад.

Векторная диаграмма является графической иллюстрацией урав-нений, описывающих процессы в АД. Для удобства сопоставления величин первичной и вторичной обмоток и изображения их в одном масштабе, а также для получения более простой схемы замещения, осуществляют приведение параметров цепи ротора к обмотке статора.

Суть приведения состоит в том, что реальный ротор с числом фаз и числом витков заменяется ротором, у которого число фаз, число витков в обмотке и обмоточный коэффициент принимаются такими же, как и у статора. При этом мощность, потери и МДС в приведённом роторе должны сохранить те же значения, что и в реальном роторе.

Так как , то ЭДС приведённого ротора будет равна:

. (1)

Так как , то

,

откуда

. (2)

Умножая (1) на (2), получим:

,

или

.

Полные мощности будут одинаковыми.

Приравняв электрические потери в обмотках приведённого и реального роторов, получим:

.

Подставив полученные значения тока из формулы (2)

,

получим

. (3)

Аналогично получим:

. (4)

Так как то необходимо выполнение равенства:

. (5)

Комплексное сопротивление приведённого ротора:

. (6)

При приведении величин реального ротора к обмотке статора следует иметь в виду:

1. для АД с фазным ротором ;

2. для АД с короткозамкнутым ротором

,

где число стержней короткозамкнутой обмотки ротора;

число пазов в роторе.

Запишем уравнения напряжений и токов для статора и приведённого ротора:

, (7)

, (8)

. (9)

На основании уравнений (7), (8) и (9) можно будет построить вектор-ную диаграмму АД. Её построение начинают с вектора потока . Намагничивающий ток опережает поток на угол .

Реактивная составляющая этого тока является намагничивающей составляющей, так как она создаёт поток . Другая составляющая обусловлена магнитными потерями в сердечнике статора, возникающими от переменного потока .

Электродвижущие силы, индуцируемые в обмотках статора

, отстают от потока на угол . Ток в цепи ротора отстаёт от ЭДС на угол 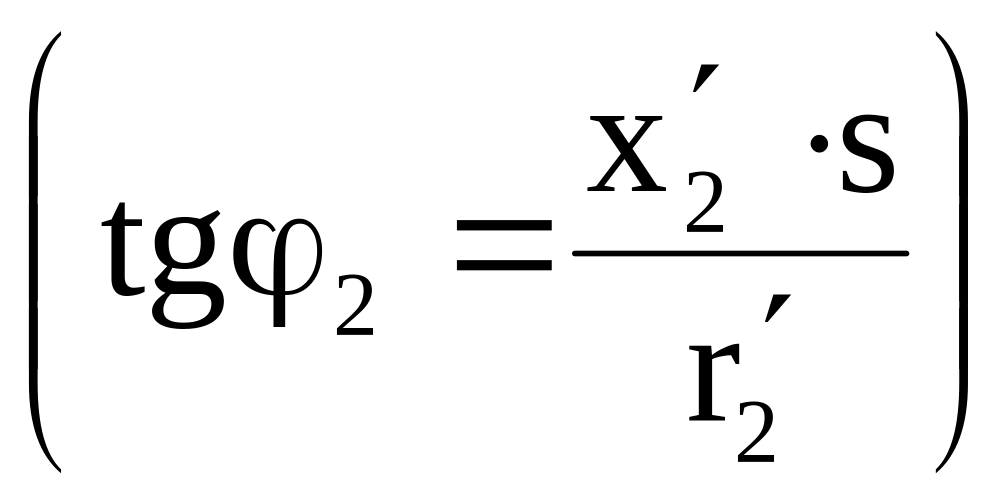и в соответствии с (8) вызывает падение напряжения в сопротивлениях , которые будут уравновешивать ЭДС .

Ток определяется по (9), а напряжение - по (7). Угол является углом сдвига между током и напряжением статора.

Мощность, забираемая из сети, будет равна:

. (10)

55 Схема замещения ад.

Для расчёта характеристик АД и исследования различных режимов его работы используются схемы замещения АД. Для получения схемы замещения запишем уравнения (7), (8) и (9) в следующем виде:

; (1)

; (2)

. (3)

Здесь принимается:

.

Решаем систему уравнений (1), (2) и (3) относительно тока , полу-чим:

. (4)

Выражению в квадратных скобках соответствует электрическая схема1.

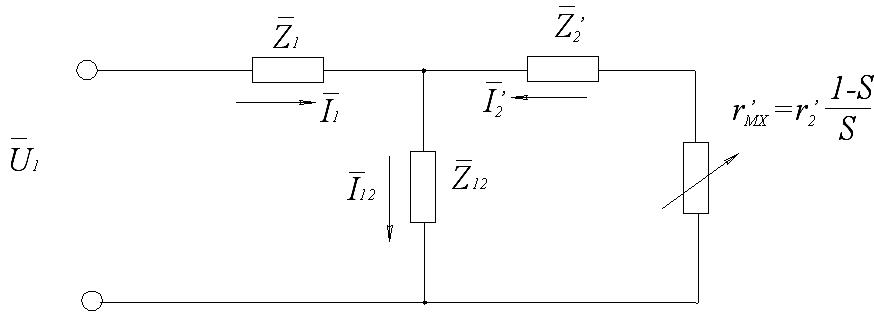
Сопротивление есть сопротивление намагничи-вающей ветви схемы замещения. Индуктивная составляющая этого сопротивления обусловлена главным магнитным потоком и является индуктивным сопротивлением взаимной индукции. Посредством сопротивления учитываются магнитные потери в сердечнике статора:

. (5)

Сопротивление зависит от подведённого напряжения . С повышением сопротивление уменьшается. Уравнение (1) для цепи статора соответствует левой части схемы замещения, а уравнение (2) для цепи ротора – правой части этой схемы. Для узловых точек справедливо уравнение (3). Параметры схемы замещения в относительных единицах для АД мощностью от нескольких кВт и выше лежат в следующих пределах:

;

;

;

.

С повышением мощности машины индуктивные сопротивления увеличиваются, а активные уменьшаются.

При расчёте характеристик АД по схеме замещения её параметры должны быть известны. Задаются скольжением s и определяют сопротивление:

.

Затем находят токи и , а по ним, используя формулы, приведённые выше, определяют мощности, электромагнитный момент, потери и так далее.

Приведённая схема замещения является Т – образной. Она полностью отражает физические процессы, происходящие в машине, но имеет узловую точку между сопротивлениями . Узловая точка усложняет расчёт токов при различных значениях сколжения.

Большое практическое применение имеет Г – образная схема замещения, в которой ветвь намагничивания подключена непосредственно на напряжение .

Из Т – образной схемы замещения следует:

. (6)

Подставив (6) в (3), получим:

,

откуда

, (7)

где - комплексный коэффициент ;

- ток синхронизма, то есть ток, потре-бляемый АД при синхронной скорости вращения ротора S=0.

Выразим ток через параметры Т – образной схемы замещения:

. (8)

Определив из Т – образной схемы замещения ток и подставив его в (8), будем иметь:

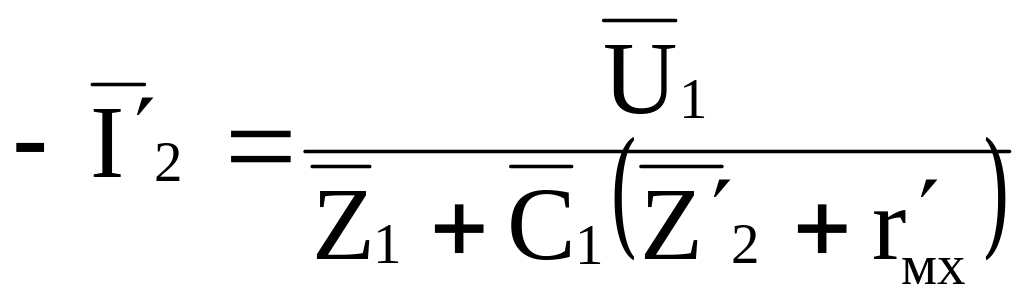. (9)

С учётом (9) перепишем уравнения (7) в виде:

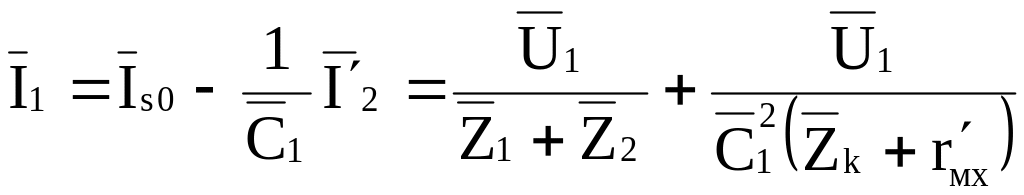, (10)

где .

Данному уравнению (10) соответствует Г – образная схема замещения следующего вида:

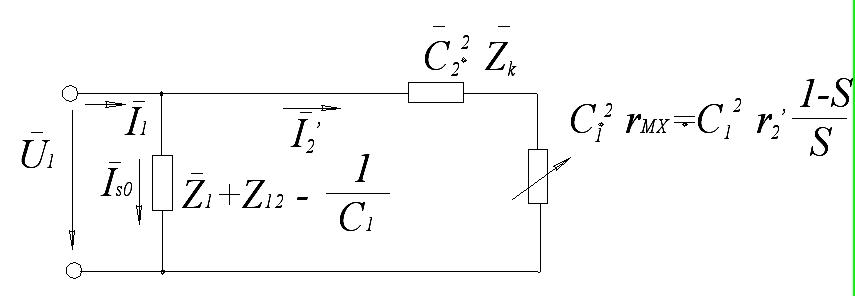
При такой схеме токи определяются независимо друг от друга делением напряжения на сопротивление соответствующей ветви. При = const ток является постоянной величиной и не зависит от скольжения.

Комплексный коэффициент :

, (11)

имеет определённый физический смысл. Умножив числитель и знаменатель на ток синхронизма , получим:

, (12)

где обратная ЭДС, индуцируемая в обмотке статора при S=0.

Для машин мощностью от нескольких кВт и выше модуль коэф-фициента равен:

,

а аргумент . Поэтому обычно принимают , а комплексный коэффициент заменяют модулем . Для практических расчётов машин средней и большой мощности можно принять . Погрешность в расчётах при этом не превышает , схема замещения будет иметь вид.

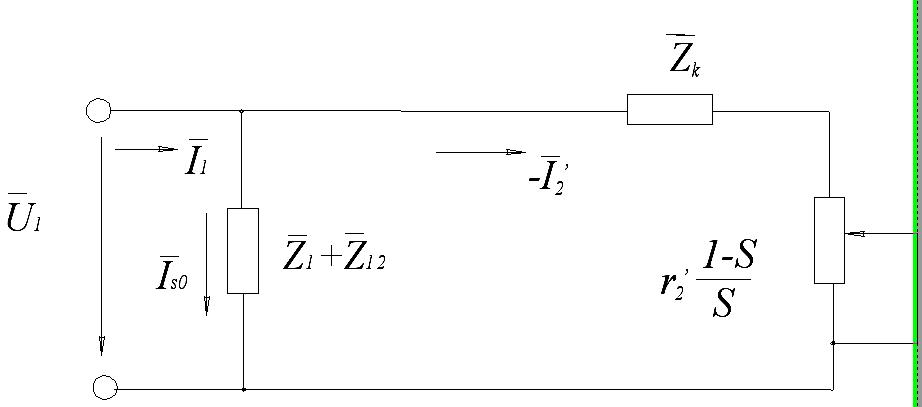
Комплексный коэффициент учитывается при анализе работы АД малой мощности.