6. Формула полной вероятности. Формула Байеса.

Пусть событие А может произойти только с одним из n несовместных событий H₁…H_n, образующих полную группу: Ø, , тогда .

Так как события и несовместны, то и ( ) и ( ) являются несовместными. Тогда по теореме сложения: .

Применяя теорему умножения к каждому слагаемому, получим формулу полной вероятности: .

Она применяется во всех случаях, когда опыт со случайным исходом распадается на два этапа: на первом учитываются условия, на втором – его результат.

События H₁, H₂,…, H_n часто называют гипотезами.

Иногда интересует, как перераспределятся вероятности гипотез после того, как событие А уже произошло: . По теореме умножения:

, .

Подставляя в знаменатель формулу полной вероятности, получим формулу Байеса: .

7. Схема независимых испытаний Бернулли.

При применении теории вероятности есть задачи, где один и тот же опыт повторяются неоднократно. В результате каждого опыта может появиться или не появится событие А, при этом интерес не к результату отдельного опыты, а число появлений события А в серии опыта. Например, если производится несколько выстрелов по одной и той же цели, интересует не результат каждого выстрела, а число попаданий. В подобных задачах требуется определить вероятность любого заданного числа появлений событий в результате серии опытов. Пусть производится последовательность независимых испытаний, в каждом из которых возможно только 2 исхода: событие А или появится или не появится, вероятность появления ,не появления , при этом .

Под элементарным событием в схеме Бернулли понимается последовательность наступлений и не наступлений события А в n испытаниях. Обозначим А={1}, ={0}. Тогда элементарный исход можно представить в виде вектора, состоящего из нулей и единиц: (1,0,…, 1).

Найдем вероятность того, что в n испытаниях событие А появится ровно m раз. Найдем сначала вероятность того, что в 3-х испытаниях событие А появится 2 раза при условии, что вероятность наступления в одном испытании равна p. При этом возможны следующие элементарные исходы (1,1,0); (0,1,1); (1,0,1).

Вероятность каждого элементарного исхода одинакова и равна p²q. Таким образом, вероятность того, что в 3-х испытаниях событие наступит 2 р.: .

Для произвольных m и n вероятность одного элементарного исхода равна p^mq^n-m . Число таких элементарных исходов равно числу способов разместить m единиц по n местам, а это по определению есть число сочетаний из n элементов по m. Получим формулу Бернулли: .

Часто интересует вероятность появления события А не ровно m раз, а от m₁ до m₂ раз включительно. Тогда она определяется по формуле:

.

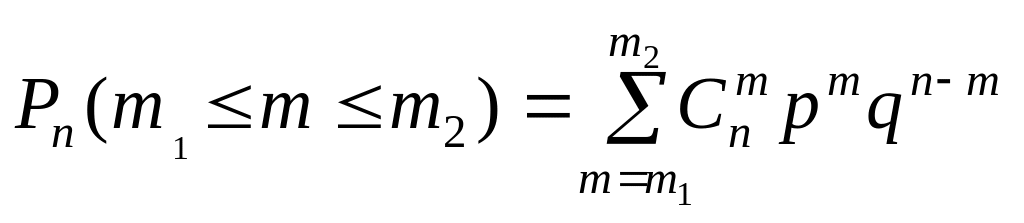8. Предельные теоремы в схеме Бернулли.

При больших n применение формулы Бернулли затруднительно из-за сложности вычисления факториалов и степеней. В этом случае используются приближенные формулы.

Рассмотрим 2 случая: 1) или . 2) p – конечно.

Теорема Пуассона: Если в схеме Бернулли , так, что - конечное число, то вероятность приближенно вычисляется по формуле Пуассона: .

Замечания: 1. – среднее число появления события А в n испытаниях. 2. Как правило, теорему Пуассона применяют, когда . 3. В конце книг по теории вероятностей имеются таблицы для подсчета вероятности по формуле для различных и m.

Локальная предельная теорема Муавра-Лапласа:

Если n , а p – конечное число из интервала (0,1), то для каждого C>0 и <C, где справедливо: , где называется плотностью нормального распределения.

Интегральная предельная теорема Муавра-Лапласа: если m есть число наступлений события в n независимых испытаниях, в каждом из которых вероятность этого события равна p, причем рє (0,1), то равномерно относительно а и b. (-∞<a<b<+∞) при n→∞ имеет место соотношение

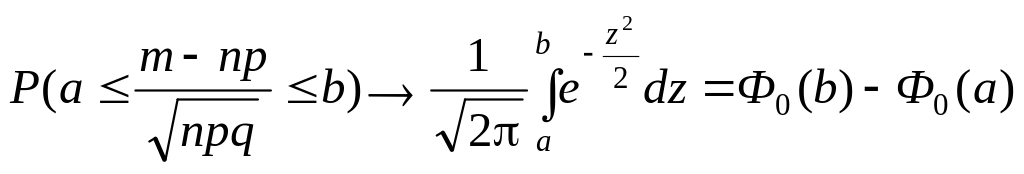, - функция Лапласа.

Замечания: 1. Ф-ция Лапласа нечетная: = - .

2. Ф-ция асимптотическая и при она быстро стремиться к 0,5. Это стремление настолько быстрое, что при можно считать равным 0,5.

3. Плотность нормального распределения - четная функция.

4. Функции , в конце книг по ТВ и МС заданы таблично.