8 Задание

1) Площадь фигуры, ограниченной графиком непрерывной функции r=r(φ) для α≤φ≤β и двумя лучами φ=α и φ=β, где φ и r – полярные координаты, вычисляется по формуле S=²φdφ

2) Если гладкая кривая задана параметрическими уравнениями x=x(t), y=y(t), t₁≤t≤t₂, то длина l ее дуги равна |l|=dt

3) Площадь криволинейной трапеции, ограниченной графиком непрерывной функции y=f(x) (f(x)≥0), двумя прямыми x=a и x=b и осью OX, вычисляется по формуле: S=(x)dx

4) Если гладкая кривая задана уравнением y=f(x), a≤x≤b и длина ее дуги l вычисляется по формуле: |l|=dx

5) Если фигура ограничена кривой, заданной параметрическими уравнениями x=x(t), y=y(t); прямыми x=a, x=b и осью OX, то ее площадь вычисляется по формуле: S=(t)x’(t)dt

6) Если гладкая кривая задана уравнением в полярных координатах r=r(φ), α≤φ≤β, то длина l ее дуги вычисляется по формуле: |l|=dφ

7) Площадь фигуры, ограниченной графиками непрерывных функций y=f₁(x) и y=f₂(x), f₁(x)≤f₂(x) и двумя прямыми x=a, x=b, определяется по формуле: S=f₂(x)-f₁(x))dx

8) Если криволинейная трапеция, ограниченная графиком непрерывной функции y=f(x), a≤x≤b, вращается вокруг оси OX, то объем тела вращения вычисляется по формуле: V=π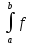²(x)dx

9) Площадь фигуры, ограниченной графиками непрерывных на [a,b] функций x=f₁(y) и x=f₂(y), f₁(y)≤f₂(y) и двумя прямыми y=a, y=b определяется по формуле: S=f₂(y)-f₁(y))dy

10) Если криволинейная трапеция, ограниченная графиком непрерывной функции y=f(x), 0≤a≤x≤b, вращается вокруг оси OY, то объем тела вращения вычисляется по формуле: V=2π|f(x)|dx

9 Задание

1) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то механический смысл интеграла (x)xdx есть статический момент дуги относительно оси Y

2) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то момент инерции I_x той дуги относительно оси OX вычисляется по формуле: I_x=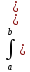f(x))²ρ(x)dx

3) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то механический смысл интеграла (x)x²dx есть момент инерции дуги кривой относительно оси Y

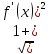4) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то статический момент M_y этой дуги относительно оси OY вычисляется по формуле: M_y=ρ(x)dx

5) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то механический смысл интеграла (x)f²(x)dx есть момент инерции кривой относительно X

6) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то координаты центра масс ивычисляются по формулам:x==(x)xdx y==f(x))ρ(x)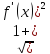dx, где l – масса дуги

7) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то механический смысл интеграла (x)f(x)dx есть стат-ий момент дуги отн-но оси X

8) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то момент инерции I_y относительно оси OY вычисляется по формуле: I_y=²ρ(x)dx

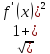9) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то механический смысл интеграла (x)f(x)dx есть стат-ий момент дуги отн-но оси X

10) Если дуга кривой задана уравнением y=f(x), a≤x≤b и имеет плотность ρ=ρ(x), то статический момент M_x этой дуги относительно оси OX вычисляется по формуле: M_x=(x)ρ(x)dx