
5 Задание
1)
Простейшей (элементарной) дробью
является 1
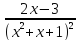
2)
Рациональная дробь
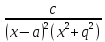 разлагается в сумму элементарных дробей
вида:
разлагается в сумму элементарных дробей
вида: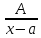 +
+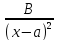 +
+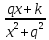
3)
Простейшей (элементарной) дробью
является 2
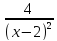
4)
Рациональная дробь
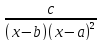 разлагается в сумму элементарных дробей
вида:
разлагается в сумму элементарных дробей
вида: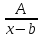 +
+ +
+
5)
Простейшей (элементарной) дробью
является 2
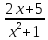
6)
Рациональная дробь
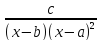 разлагается в сумму элементарных дробей
вида:
разлагается в сумму элементарных дробей
вида: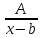 +
+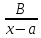 +
+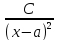
7)
Простейшей (элементарной) дробью
является 2
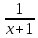
8)
Интеграл
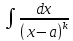 равен, если 1)k=1,
то ln|x-a|+C,
2)k>1,
то
равен, если 1)k=1,
то ln|x-a|+C,
2)k>1,
то
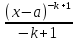 +C
+C
9)
Рациональная дробь
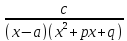 ,
гдеp2-4q<0,
разлагается в сумму элементарных дробей
вида
,
гдеp2-4q<0,
разлагается в сумму элементарных дробей
вида
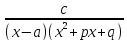 =
=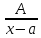 +
+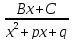
10)
Отношение двух многочленов
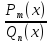 ,
гдеPm(x)=b0+b1x+..+Bmxm,
Qn(x)=a0+a1x+..+anxn,
bm≠0,
an≠0,
m≥0,
n≥1
при m<n
называется правильной рациональной
дробью
,
гдеPm(x)=b0+b1x+..+Bmxm,
Qn(x)=a0+a1x+..+anxn,
bm≠0,
an≠0,
m≥0,
n≥1
при m<n
называется правильной рациональной
дробью
6 Задание
1)
Интеграл
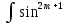 xcosnxdx,
где m
– целое неотрицательное число, сводится
к табличному с помощью замены t=cosx;
dt=-sinxdx,
с использованием sin2x+cos2x=1
xcosnxdx,
где m
– целое неотрицательное число, сводится
к табличному с помощью замены t=cosx;
dt=-sinxdx,
с использованием sin2x+cos2x=1
2)
Интегралы вида
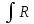 (cosx,sinx)dx,
где R(x,y)
– рациональная функция, сводятся к
интегрированию рациональных дробей с
помощью универсальной подстановки
t=tg
(cosx,sinx)dx,
где R(x,y)
– рациональная функция, сводятся к
интегрированию рациональных дробей с
помощью универсальной подстановки
t=tg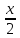 ,
причем sinx,
cosx,
и dx
соответственно равны sinx=
,
причем sinx,
cosx,
и dx
соответственно равны sinx=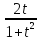 ,cosx=
,cosx=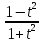 ,dx=
,dx=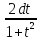
3)
Интегралы
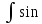 2mxcos2nxdx,
где m
и n
– натуральные числа, вычисляются с
помощью тригонометрических формул
вида: 1) cos2x=
2mxcos2nxdx,
где m
и n
– натуральные числа, вычисляются с
помощью тригонометрических формул
вида: 1) cos2x=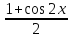 ,
2)sin2x=
,
2)sin2x=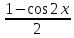 ,
3)sinxcosx=
,
3)sinxcosx=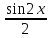 ,
понижающих степень подинтегрального
выражения.
,
понижающих степень подинтегрального
выражения.
4)
Для вычисления интеграла
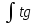 mxdx,
(m=2,3,4..)
используется тригонометрическая
формула tg2x=
mxdx,
(m=2,3,4..)
используется тригонометрическая
формула tg2x= -1
-1
5)
Интеграл вида
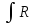 (x,
(x,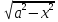 )dx,
где R(x,y)
– рациональная функция, a
– действительное положительное число,
приводится к интегралу
)dx,
где R(x,y)
– рациональная функция, a
– действительное положительное число,
приводится к интегралу
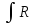 (sint,cost)dt
тригонометрической подстановкой:
x=asint,
dx=acostdt
(sint,cost)dt
тригонометрической подстановкой:
x=asint,
dx=acostdt
6)
Интегралы вида
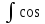 2m+1xsinnxdx,
где m
– целое неотрицательное число, сводятся
к табличному с помощью внесения под
знак дифференц. cosx
2m+1xsinnxdx,
где m
– целое неотрицательное число, сводятся
к табличному с помощью внесения под
знак дифференц. cosx
7)
Интеграл
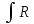 (x,
(x,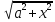 )dx,
где R(x,y)
– рациональная функция, a
– действительное положительное число,
приводится к интегралу
)dx,
где R(x,y)
– рациональная функция, a
– действительное положительное число,
приводится к интегралу
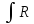 (sint,cost)dt
тригонометрической подстановкой вида:
x=atgt,
dx=
(sint,cost)dt
тригонометрической подстановкой вида:
x=atgt,
dx=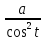 dt
dt
8)
Для вычисления интеграла
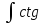 mxdx,
где m
– натуральное число большее 1, используется
тригонометрическая формула: ctg2x=
mxdx,
где m
– натуральное число большее 1, используется
тригонометрическая формула: ctg2x= -1
-1
9)
Интеграл
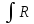 (x,
(x,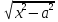 )dx,
где R(x,y)
– рациональная функция, a
– действительное положительное число,
приводится к интегралу
)dx,
где R(x,y)
– рациональная функция, a
– действительное положительное число,
приводится к интегралу
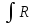 (sint,cost)dt
тригонометрической подстановкой: x=
(sint,cost)dt
тригонометрической подстановкой: x=
10)
Для вычисления интеграла
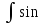 axcosbxdx,
где a≠0,
b≠0
применяется тригонометрическая формула:
sinaxcosbx=
axcosbxdx,
где a≠0,
b≠0
применяется тригонометрическая формула:
sinaxcosbx=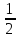 [sin(a-b)x+sin(a+b)x]
[sin(a-b)x+sin(a+b)x]
7 Задание
1)
Если f(x)
непрерывная на [a,b]
функция и F’(x)=f(x)
на [a;b],
то по формуле Ньютона-Лейбница
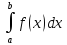 равенF(x)|
равенF(x)| =F(b)-F(a)
=F(b)-F(a)
2)
По теореме о среднем значении для
непрерывной на отрезке [a,b]
функции f(x)
существует точка c∈(a,b)
такая, что
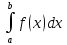 равенf(c)(b-a)
равенf(c)(b-a)
3)
По теореме об оценке определенного
интеграла, если f(x)
непрерывна на [a,b],
m
– наименьшее, M
– наибольшее значения f(x)
на [a,b],
то для
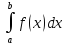 выполняются неравенства:m(b-a)≤
выполняются неравенства:m(b-a)≤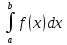 ≤M(b-a)
≤M(b-a)
4)
По теореме о среднем значении для
непрерывной на отрезке [a,b]
функции f(x)
существует точка c∈(a,b)
такая, что выражение
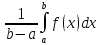 равноf(c)
равноf(c)
5)
Если f(x)
непрерывная на [a,b]
функция и F’(x)=f(x)
на [a,b],
то по формуле Ньютона-Лейбница
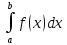 равенF(x)|
равенF(x)|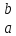 =F(b)-F(a)
=F(b)-F(a)
6)
Если фун-ия f(x)
непрерывна и положительна на отрезке
[a,b],
то для числа с=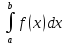 справедливо3
c>0
справедливо3
c>0
7)
Если F(x)
– первообразная для непрерывной на
[a,b]
функции f(x)
то формула Ньютона-Лейбница имеет вид:
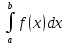 =F(b)-F(a)
=F(b)-F(a)
8)
Если функции f(x)
и φ(x)
интегрируемы на отрезке [a,b],
удовлетворяют на нем неравенству
f(x)≤φ(x)
A=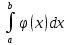 ,B=
,B=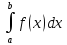 (a≤b),
то 4
A≥B
(a≤b),
то 4
A≥B
9)
Если
функция f(x)
непрерывна на отрезке [a,b],
то функция F(x)=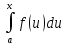 дифференцируема на (a,b)
и F’(x)
равна f(x)
дифференцируема на (a,b)
и F’(x)
равна f(x)
10)
Если f(x)
и |f(x)|
интегрируемы на [a,b]
A=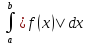 ,B=
,B=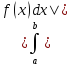 (a≤b),
то 5
A≥B
(a≤b),
то 5
A≥B
