Вопрос 6

Если в уравнение y``+py`+qy=x²e^^xкоэффициенттакой, что²+p+q0, то его частное решение имеет вид:= (Ax²+Bx+C)e^^x
Если aib не является корнем уравнения k²+pk+q=0, то частное решение уравнения y``+py`+qy=e^^x(xcosbx+sinbx) имеет вид: =e^^x(Ax+B)cosbx+(Cx+D)sinbx.
Если - простой корень уравнения k²+pk+q =0, то частное решение уравнениеy``+py`+qy=e^^xимеет вид:=Axe^^x
Если aibявляется корнем уравненияk²+pk+q=0, то частное решение уравненияy``+py`+qy=e^^x(cosbx+xsinbx) имеет вид:=e^^xx(Acosbx+(Bx+C)sinbx).
Если - кратный корень уравнения k²+pk+q =0, то частное решение уравнениеy``+py`+qy=xe^^xимеет вид: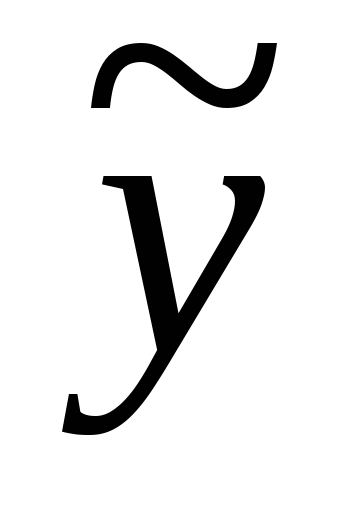=x²e^^x(Ax+B)).
Если aibявляется корнем уравненияk²+pk+q=0, то частное решение уравненияy``+py`+qy=e^^xxcosbxимеет вид:=e^^xx((Ax–B)cosbx+(Cx+D)sinbx)
Если - простой корень уравнения k²+pk+q =0, то частное решение уравнениеy``+py`+qy= x²e^^xимеет вид:=xe^^x(Ax²+Bx+C)
Если aibкореyуравненияk²+pk+q=0, то частное решение уравненияy``+py`+qy=e^^xxsinbxимеет вид:=e^^xx((Ax+B)cosbx+(Cx+D)sinbx)
Если - кратный корень уравнения k²+pk+q =0, то частное решение уравнениеy``+py`+qy=x²e^^xимеет вид: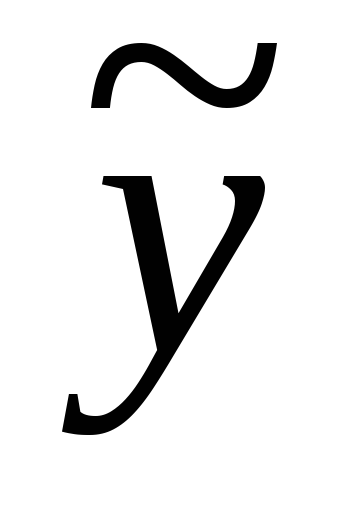=x²e^^x(Ax²+Bx+C)).
Если aibявляется корнем уравненияk²+pk+q=0, то частное решение уравненияy``+py`+qy=e^^xcosbxимеет вид:=xe^^x(Acosbx+Bsinbx)

Вопрос 7

Если y₁,y₂,y₃являются функциями отx, то определитель Вронского имеет вид:W=
Если функции y₁иy₂– линейно зависимы на отрезке [a,b], то при любомx[a,b] для определителя ВронскогоW(y_1,y₂) верноW=0
Если определитель Вронского W(y₁,y₂)0 хотя бы в одной точке интервала (a,b), то функцииy₁иy₂на интервале (a,b) линейно независимы.
Если функции y₁иy₂– линейно зависимы на отрезке [a,b], то при любомx[a,b] то определитель ВронскогоW(y_1,y₂)=0
Если определитель Вронского W(y₁,y₂) =0 на интервала (a,b), то функцииy₁иy₂на интервале (a,b) линейно зависимы.
Если для решения y₁(x),y₂(x),x[a,b] уравнение y``+py`+qy=0 определитель Вронского W(x₀)=0, (x₀[a,b]), то функцииy_{1 и}y₂линейно зависимы.
Если y₁иy₂– фундументальная система решений уравнения y``+py`+qy=0, аC₁`(x) и С₂`(x) есть решения системы, то y=С₁(x)y₁+ С₂(x)y₂является общим решением уравнения y``+py`+qy=f(x).
Если для решения y₁(x),y₂(x),x[a,b] уравнение y``+py`+qy=0 определитель Вронского W(x₀)0, (x₀[a,b]), то функцииy_{1 и}y₂линейно независимы.
Если y₁,y₂являются функциями отx, то определитель Вронского имеет вид:W=.
Если решения y₁,y₂решения уравнения y``+py`+qy=0 линейно зависимы на [a,b], то определитель Вронского W(x) для любогоx[a,b] равен 0

Вопрос 8

Согласно методу вариации произвольных постоянных, если y₀=C₁y₁+C₂y₂– общее решение уравнения y``+py`+q=0, то общее решение уравнения y``+py`+q=f(x) имеет вид:y=C₁(x)y₁+C₂(x)y₂, где С₁(x) иC₂(x)y₂определяются из системы.
Если ₁и₂– соответственно частное решение уравнений y``+py`+qy=f₁(x), y``+py`+qy=f₂(x), то сумма₁+₂есть частное решение y``+py`+qy=f₁(x)+f₂(x)
Если y₁иy₂соответственно частное решение уравнений y``+py`+qy=0, то суммаy₁+y₂есть также решение этого уравнения.
Если y₁иy₂– фундументальная система решений уравнения y``+py`+qy=0, аC₁`(x) и С₂`(x) есть решения системы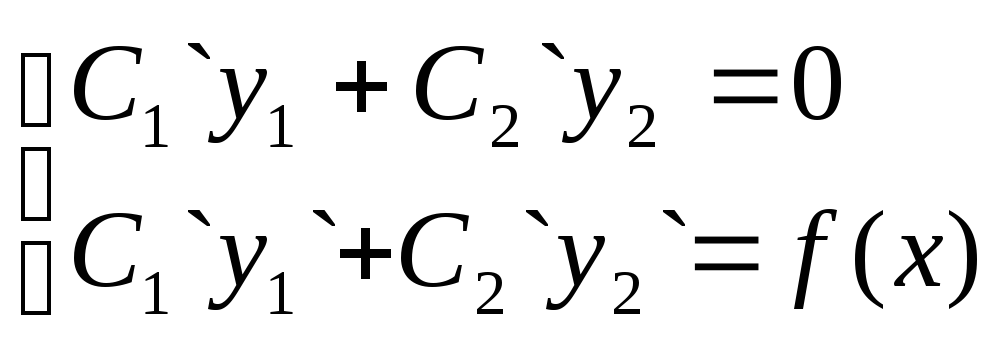, то общее решение уравнения y``+py`+qy=f(x) имеет вид: y=С₁(x)y₁+ С₂(x)y₂
Если y₁иy₂- линейно независимые решения уравненияy``+py`+qy=0, то его общее решение имеет вид:y=С₁(x)y₁+ С₂(x)y_2.
Систему можно светси к дифференциальному уравнению вида:порядка 2.
Если решения y₁,y₂уравнения y``+py`+qy=0 линейно независимы на [a,b], то для любогоx[a,b] определитель Вронского не равен 0(W(x)0)
Согласно принципу суперпозиции, частное решение уравненияy``+py`+qy=f₁(x)+f₂(x) представимо в виде суммы₁+₂, где₁и₂– частные решения уравнений y``+py`+qy=f₁(x), y``+py`+qy=f₂(x) соответственно.
Если y₀= общее решение уравненияy``+py`+qy=0,- частное решение уравненияy``+py`+q=f(x), то общее решение неоднородного уравнения имеет вид:y=y₀+.
Систему можно светси к дифференциальному уравнению вида:порядка 3.