
5 Задание
Если корни характеристического уравнения k1,k2,k3 действительные и такие, что k1=k2 и k1k3, то общее решение уравнения y```+py``+qy`+ry=0 (p,q,r – const) имеет вид: y=C1
 +xC2
+xC2 +C3
+C3
Если корни характеристического уравнения k1,k2 действительные и различны, то общее решение уравнения y``+py`+qy=0 (p,q– const) имеет вид: y=C1
 +C2
+C2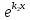 .
.Если корни характеристического уравнения такие, что k1,2=aib и k3 действителен, то общее решение уравнения y```+py``+qy`+ry=0 (p,q,r– const) имеет вид: y=C1
 +eax(c2cosbx+c3sinbx)
+eax(c2cosbx+c3sinbx)
Для диф. уравнения y```+py``+qy`+ry =0 (p,q,r– const) характеристическое уравнение имеет вид: λ3+pλ 2+qλ +r=0
Для диф. уравнения y``+py`+qy =0 (p,q– const) характерист-кое урав-ие имеет вид: λ2+pλ+q=0
Если корни характеристического уравнения k1 и k2 действительные и равны(k1=k2), то общее решение уравнения y``+py`+qy=0 (p,q– const) имеет вид: y=C1
 +xC2
+xC2 .
.Если корни характеристического уравнения k1,k2,k3 действительны и различны, то общее решение уравнения y```+py``+qy`+ry=0 (p,q,r– const) имеет вид: y=C1
 +C2
+C2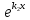 +C3
+C3
Если корни характеристического уравнения такие, что k1,2=aib, то общее решение уравнения y``+py`+qy =0 (p,q– const) имеет вид: y=eax(c1cosbx+c2sinbx)
Если корни характеристического уравнения k1,k2,k3 действительны и равны(k1=k2=k3), то общее реш-ие урав-ия y```+py``+qy`+ry=0 (p,q,r– const) имеет вид: y=C1
 +xC2
+xC2 +
xC3
+
xC3
Линейное однородное диф. уравнение второго порядка с постоянными коэффициентами имеет вид: y``+py`+qy =0
6 Задание
Если в уравнение y``+py`+qy=x2ex коэффициент такой, что 2+p+q0, то его частное решение имеет вид:
 =
(Ax2+Bx+C)ex
=
(Ax2+Bx+C)exЕсли a+bi не является корнем уравнения k2+pk+q=0, то частное решение уравнения y``+py`+qy=ex(xcosbx+sinbx) имеет вид:
 =ex((Ax+B)cosbx+(Cx+D)sinbx)
=ex((Ax+B)cosbx+(Cx+D)sinbx)Если - простой корень уравнения k2+pk+q =0, то частное решение уравнения y``+py`+qy=ex имеет вид:
 =Axex
=AxexЕсли a+bi является корнем уравнения k2+pk+q=0, то частное решение уравнения y``+py`+qy=ex(cosbx+xsinbx) имеет вид:
 =exx(Acosbx+(Bx+C)sinbx).
=exx(Acosbx+(Bx+C)sinbx).Если - кратный корень уравнения k2+pk+q =0, то частное решение уравнения y``+py`+qy=xex имеет вид:
 =x2ex(Ax+B).
=x2ex(Ax+B).Если a+ib является корнем уравнения k2+pk+q=0, то частное решение уравнения y``+py`+qy=exxcosbx имеет вид:
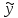 =exx((Ax+B)cosbx+(Cx+D)sinbx)
=exx((Ax+B)cosbx+(Cx+D)sinbx)Если - простой корень уравнения k2+pk+q =0, то частное решение уравнения y``+py`+qy= x2ex имеет вид:
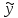 =xex(Ax2+Bx+C)
=xex(Ax2+Bx+C)Если a+ib корень уравнения k2+pk+q=0, то частное решение уравнения y``+py`+qy=exxsinbx имеет вид:
 =exx((Ax+B)cosbx+(Cx+D)sinbx)
=exx((Ax+B)cosbx+(Cx+D)sinbx)Если - кратный корень уравнения k2+pk+q =0, то частное решение уравнения y``+py`+qy=x2ex имеет вид:
 =x2ex(Ax2+Bx+C)).
=x2ex(Ax2+Bx+C)).Если a+ib является корнем уравнения k2+pk+q=0, то частное решение уравнения y``+py`+qy=excosbx имеет вид:
 =xex(Acosbx+Bsinbx)
=xex(Acosbx+Bsinbx)
