Содержание:
1.Приближенные числа и действия с ними.
2. Понятие относительной погрешности.
3. Понятие конечных разностей функции.
4. Приближенное решение обыкновенных дифференциальных уравнений.
5. Численное интегрирование.
6. Численное дифференцирование.
1. Приближенные числа и действия с ними.
Модуль разности между точным числом и его приближенным значением называется абсолютной погрешностью приближенного значения числа.
Абсолютная погрешность суммы и разности приближенных чисел равна сумме абсолютных погрешностей.
Пример1 При вычислении выражения
![]() данные
в условии задачи значения
данные
в условии задачи значения
![]() и
и
![]() округлили
до целых значений и получили
округлили
до целых значений и получили
![]() Тогда
абсолютная погрешность полученного
результата равна …
Решение:
Значит, абсолютная
погрешность числа 20 равна
Тогда
абсолютная погрешность полученного
результата равна …
Решение:
Значит, абсолютная
погрешность числа 20 равна ![]() и абсолютная погрешность числа 5
равна
и абсолютная погрешность числа 5
равна ![]() .
Тогда абсолютная погрешность числа 25
будет равна
.
Тогда абсолютная погрешность числа 25
будет равна ![]()
При вычислении выражения
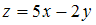 данные
в условии задачи значения
данные
в условии задачи значения
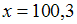 и
и
 округлили
до целых значений и получили
округлили
до целых значений и получили
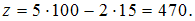 Тогда
абсолютная погрешность полученного
результата равна …1,9
Тогда
абсолютная погрешность полученного
результата равна …1,9
2. Понятие относительной погрешности.
Относительная погрешность приближенного положительного числа равна отношению абсолютной погрешности числа к точному значению этого числа. Так как точное значение числа, как правило, неизвестно, то под относительной погрешностью понимают отношение абсолютной погрешности числа к его приближенному значению.
Относительная погрешность произведения приближенных чисел равна сумме относительных погрешностей сомножителей.
Пример1 Известно,
что стороны прямоугольника равны 122
см и
58 см.
Для упрощения
вычислений эти числа
были округлены до 120
см и
60 см.
Была
найдена площадь S = 120∙60 = 7200 кв. см.
Полученный результат имеет относительную
погрешность равную …Решение:
Тогда
относительные погрешности чисел 120 и
60 равны соответственно
![]()
![]()
Для вычисления площади стены измерили ее длину и ширину. Получили 603 см и 245 см. Округлив полученные результаты до 600 см и 250 см соответственно, вычислили площадь стены
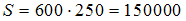 (кв. см.)
Тогда
относительная погрешность полученного
результата равна …0,025
(кв. см.)
Тогда
относительная погрешность полученного
результата равна …0,025Вычислили значение функции
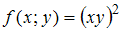 при
при
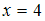 и
и
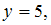 получили
результат,
равный 400. Известны относительные
погрешности чисел 4 и 5:
получили
результат,
равный 400. Известны относительные
погрешности чисел 4 и 5:
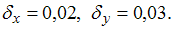 Тогда
относительная погрешность полученного
результата равна …
Тогда
относительная погрешность полученного
результата равна …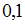
Известно, что ребра прямоугольного параллелепипеда равны 103 см, 21 см и 98 см. Для упрощения вычислений эти числа округлили до 100 см, 20 см и 100 см соответственно. Нашли объем:
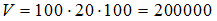 (куб. см.)
Полученный
результат имеет относительную
погрешность, равную …0,1
(куб. см.)
Полученный
результат имеет относительную
погрешность, равную …0,1Вычислили значение функции
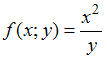 при
при
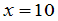 и
и
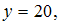 получили
результат,
равный 5. Известны относительные
погрешности чисел 10 и 20:
получили
результат,
равный 5. Известны относительные
погрешности чисел 10 и 20:
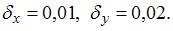 Тогда
относительная погрешность полученного
результата равна …
Тогда
относительная погрешность полученного
результата равна …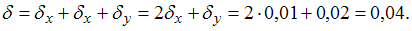
3. Понятие конечных разностей функции.
Задание функции y = f(x) в виде набора пар чисел (xi, yi) называется табличным заданием функции
xi |
yi |
x0 |
y1 |
x1 |
y2 |
x2 |
y3 |
••• |
••• |
xn |
yn |
Таблицы бывают с постоянным и переменным шагом. Если таблица имеет постоянный шаг, то
x1 – x0 = x2 – x1 = … = xn – xn-1 = h
xi = x0 + ih, i = 0, 1, 2, …, n
Если таблица имеет переменный шаг, то
x1 – x0 ≠ x2 – x1 ≠ … ≠ xn – xn-1
Для таблиц с постоянным шагом вводится
понятие конечных разностей.
![]() Для нахождения конечных разностей можно
воспользоваться следующей схемой:
для
вычисления значений в i
строке
следующего столбца таблицы нужно вычесть
из числа, стоящего в i+1
строке, число, стоящее в i
строке в предыдущем столбце.
Для нахождения конечных разностей можно
воспользоваться следующей схемой:
для
вычисления значений в i
строке
следующего столбца таблицы нужно вычесть
из числа, стоящего в i+1
строке, число, стоящее в i
строке в предыдущем столбце.
Xi |
Yi |
∆Y |
∆2Y |
… |
∆nY |
||||||
X0 |
Y0 |
…
|
|
|
|
||||||
X1 |
Y1 |
|
|||||||||
X2 |
Y2 |
… |
|||||||||
… |
… |
|
|||||||||
Xn-1 |
Yn-1 |
|
|||||||||
Xn |
Yn |
|
Где
∆Yi=Yi+1-Yi конечная разность первого порядка
∆2Yi=∆Yi+1-∆Yi конечная разность второго порядка
∆3Yi=∆2Yi+1-∆2Yi конечная разность третьего порядка и т.д.
Пример1: функция f(x) задана таблично. Составить конечные разности.
Xi |
Yi |
∆Y |
∆2Y |
∆3Y |
|||
5 |
9 |
|
0 |
1 |
|||
7 |
12 |
||||||
9 |
15 |
1 |
|||||
11 |
19 |
Пример2:Для
некоторой функции
![]() известна
таблица ее значений
известна
таблица ее значений
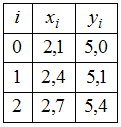 .
Тогда
конечная разность
.
Тогда
конечная разность
![]() равна …
Решение:
Эта
схема соответствует формуле.
Тогда
получим:
равна …
Решение:
Эта
схема соответствует формуле.
Тогда
получим:
![]()
![]()
![]()
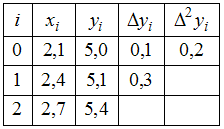 .
.
Дана таблица для вычисления конечных разностей некоторой функции:
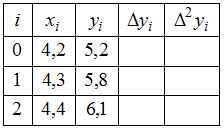 .
Конечная разность
.
Конечная разность
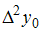 равна …
равна …
Для некоторой функции известна таблица ее значений
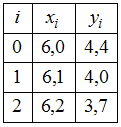 .
Тогда
конечная разность
равна …0,1
.
Тогда
конечная разность
равна …0,1Для некоторой функции известна таблица ее значений
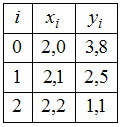 .
Тогда
конечная разность
равна …
.
Тогда
конечная разность
равна …