
Вопрос 18-19, 21-26 , 28 Понятие числового ряда
Пусть
числа
![]()
члены некоторой бесконечной числовой
последовательности. Тогда выражение
вида
члены некоторой бесконечной числовой
последовательности. Тогда выражение
вида
![]() (1)
(1)
называется
числовым рядом. Здесь
![]()
общий член ряда
общий член ряда
Рассмотрим для числового ряда (1) суммы его первых членов:
![]() Будем
называть их частичными суммами и
обозначим соответственно
Будем
называть их частичными суммами и
обозначим соответственно ![]() (2)
(2)
Ряд
(1) называется сходящимся, если
последовательность его частичных сумм
(2) имеет конечный предел. Этот
предел ![]() называется
суммой ряда.
называется
суммой ряда.
Сумму ряда
![]() .
.
Необходимый признак сходимости ряда
Если
ряд сходится, то
![]() un=0.
un=0.
Критерий сходимости положительных рядов (критерий Коши)
Положительный ряд сходится ,когда последовательность его частичных сумм ограничена сверху
Признаки сравнения рядов
Даны
два ряда
 и
и
![]() −
такие, что
−
такие, что
![]() для
всех n. Тогда справедливы следующие
признаки:
для
всех n. Тогда справедливы следующие
признаки:
Если
сходится,
то
![]() также
сходится;
также
сходится;
Если расходится, то также расходится.
Признак сравнения в предельной форме.
Даны
два ряда с положительными членами
![]() и
и![]() и пусть существует конечный и не равный
нулю
и пусть существует конечный и не равный
нулю
![]() .
Тогда оба ряда сходятся или расходятся
одновременно
.
Тогда оба ряда сходятся или расходятся
одновременно
Радикальный признак Коши — признак сходимости числового ряда:
-
Если для числового ряда

с неотрицательными членами существует такое число
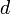 ,
,
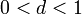 ,
что, начиная с некоторого номера,
выполняется неравенство
,
что, начиная с некоторого номера,
выполняется неравенство
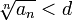 ,
то данный ряд сходится.
,
то данный ряд сходится.
Признак Д’Аламбера
Если для числового ряда
![]()
существует
такое число
![]() ,
,
![]() ,
что начиная с некоторого номера
выполняется неравенство
,
что начиная с некоторого номера
выполняется неравенство
![]()
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
![]()
то ряд расходится.
Интегральный признак Коши — Маклорена
Формулировка теоремы
-
Пусть для функции f(x) выполняется:
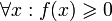 (функция
принимает неотрицательные значения)
(функция
принимает неотрицательные значения)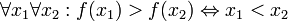 (функция
монотонно убывает)
(функция
монотонно убывает)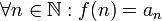 (соответствие
функции ряду)
(соответствие
функции ряду)
Тогда ряд и несобственный интеграл
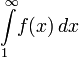 сходятся
или расходятся одновременно.
сходятся
или расходятся одновременно.
Абсолютная и условная сходимость
Ряд
называется
абсолютно
сходящимся,
если ряд
![]() также
сходится.
Если ряд
сходится
абсолютно, то он является сходящимся
(в обычном смысле). Обратное утверждение
неверно.
Ряд
называется
условно
сходящимся,
если сам он сходится, а ряд, составленный
из модулей его членов, расходится.
также
сходится.
Если ряд
сходится
абсолютно, то он является сходящимся
(в обычном смысле). Обратное утверждение
неверно.
Ряд
называется
условно
сходящимся,
если сам он сходится, а ряд, составленный
из модулей его членов, расходится.
Вопрос 29
Признак Лейбница
Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. Пусть {an} является числовой последовательностью, такой, что
1.
an+1
< an
для всех n;
2.
![]() .
.
Тогда
знакочередующиеся ряды
![]() и
и
![]() сходятся.
сходятся.
Вопрос 30
Признак Абеля сходимости числовых рядов
Числовой
ряд
![]() сходится,
если выполнены следующие условия:
сходится,
если выполнены следующие условия:
Последовательность
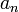 монотонна
и ограничена.
монотонна
и ограничена.Числовой ряд
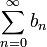 сходится.
сходится.
Признак Дедекинда
Ряд
ряд
частичные
суммы ряда
|
Вопрос 31
Перестановка членов ряда
Если ряд сходится абсолютно, то любой ряд, полученный из него перестановкой членов, также сходится абсолютно и имеет ту же сумму, что и исходный ряд
Вопрос 32
Пусть
ряд
![]() сходится
условно, тогда для любого числа S
сходится
условно, тогда для любого числа S![]() можно так поменять порядок суммирования,
что сумма нового ряда будет равна S.
можно так поменять порядок суммирования,
что сумма нового ряда будет равна S.
Вопрос 33-34
Функциональный ряд состоит из ФУНКЦИЙ:
![]()
Степенной
ряд – это
ряд, в общий член
![]() которого
входят целые
положительные степени
независимой переменной
которого
входят целые
положительные степени
независимой переменной
![]()
Степенной
ряд
![]() .
.
Переменная
может
принимать любое
действительное значение
от «минус бесконечности» до «плюс
бесконечности». Подставим в общий член
ряда несколько произвольных значений
«икс»:
Если
![]() ,
то
,
то
![]() Если
Если
![]() ,
то
,
то
![]() Если
Если
![]() ,
то
,
то
![]() И
так далее.
И
так далее.
Очевидно,
что, подставляя в
![]() то
или иное значение «икс», мы получаем
различные числовые ряды. Некоторые
числовые ряды будут сходиться, а некоторые
расходиться. множество
значений «икс»,
при котором степенной ряд
будет
сходиться
и называется областью
сходимости ряда.
то
или иное значение «икс», мы получаем
различные числовые ряды. Некоторые
числовые ряды будут сходиться, а некоторые
расходиться. множество
значений «икс»,
при котором степенной ряд
будет
сходиться
и называется областью
сходимости ряда.
Радиус
сходимости
это половина
длины
интервала сходимости:
![]()

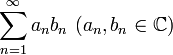 сходится,
если:
сходится,
если: