Вопрос 9-10

Общее уравнение. Уравнение плоскости, проходящей через данную точку и имеющей данный нормальный вектор

В декартовых координатах каждая плоскость определяется уравнением первой степени и каждое уравнение первой степени определяет плоскость.

Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение

(1)

определяет плоскость, проходящую через точку и имеющей нормальный вектор .

Раскрывая в уравнении (1) скобки и обозначая число буквой D, представим его в виде

.

Это уравнение называется общим уравнением плоскости.

Вопрос 11

Каноническое уравнение прямой в пространстве

Прямая проходит через точку M₁ (x₁, y₁, z₁) и параллельна вектору (m ,n, l).

- каноническое уравнение прямой в пространстве.

Параметрическое уравнение прямой.

 Это векторное уравнение может быть представлено в координатной форме:

Вопрос 12 Условие параллельности и перпендикулярности прямых и плоскостей.

Плоскости α₁ и α₂, заданные уравнениями:

Две плоскости α₁ и α₂ параллельны, когда их нормальные векторы и параллельны, а значит

Если параллельны , или

Прямые

Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.

 

            Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.

Вопрос 13-17

Комплексные числа

Комплексным числом  называется число вида , где  и  – действительные числа,  – так называемая мнимая единица. Число  называется действительной частью ( ) комплексного числа , число  называется мнимой частью ( ) комплексного числа .

Построим на комплексной плоскости следующие комплексные числа: , , , , , , ,

Комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.

Действия с комплексными числами мало чем отличаются от обычной алгебры.

Например сложение

Любое комплексное число (кроме нуля)  можно записать в тригонометрической форме:

, где  – это модуль комплексного числа, а  – аргумент комплексного числа.

Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что :

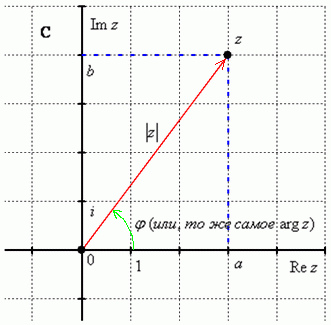
Модулем комплексного числа  называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа  стандартно обозначают:  или

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений «а» и «бэ».

Аргументом комплексного числа  называется угол  между положительной полуосью действительной оси  и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

Формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень  справедлива формула:

Извлечение корней из комплексных чисел

Извлекается два корня:

Они называют сопряженными комплексными корнями.