
- •1.2. Прямоугольная система координат на плоскости.
- •1.3. Полярная система координат.
- •1.4. Связь между полярными и декартовыми координатами.
- •1.5. Расстояние между двумя точками.
- •Деление отрезка в данном отношении.
- •1.7. Площадь треугольника.
- •2.1. Уравнение линии на плоскости.
- •2.2. Уравнение прямой с угловым коэффициентом.
- •2.3. Уравнение прямой по точке и угловому коэффициенту.
- •2.4. Уравнение прямой, проходящей через две данные точки.
- •2.5. Общее уравнение прямой.
- •2.6. Уравнение прямой в отрезках на осях координат.
- •2.7. Угол между прямыми на плоскости.
- •2.8. Условия параллельности и перпендикулярности прямых на плоскости.
- •3.1. Расстояние от точки до прямой.
- •3.2. Взаимное расположение двух прямых на плоскости.
- •4.1. Эллипс. Окружность.
- •4.2. Гипербола.
- •4.3. Парабола.
- •5.1 Понятие о матрице.
- •5.2. Сложение и вычитание матриц.
- •5.3. Умножение матрицы на число.
- •5.4. Умножение матриц.
- •5.5. Транспонирование матрицы.
- •5.6. Элементарные преобразования строк матрицы.
- •5.7. Ступенчатая матрица. Ранг матрицы.
- •6.1. Определители второго порядка.
- •6.2. Определители третьего порядка.
- •6.3. Определитель n-го порядка (n n).
- •6.4. Свойства определителей.
- •6.5. Обратная матрица.
- •7.1. Систем линейных уравнений.
- •7.2. Критерий совместности системы линейных уравнений.
- •7.3. Метод Гаусса решения системы линейных уравнений.
- •7.4. Правило Крамера решения систем линейных уравнений.
- •7.5. Матричный метод решения систем линейных уравнений.
- •8.1. Прямоугольная декартова система координат в пространстве.
- •8.2. Понятие вектора.
- •8.3. Линейные операции над векторами.
- •8.4. Проекция вектора на ось.
- •8.5. Координаты вектора.
- •8.6. Длина вектора. Расстояние между точками в пространстве.
- •8.7. Деление отрезка в данном отношении.
- •9.1. Разложение вектора по базисным векторам.
- •9.2. Скалярное произведение векторов.
- •9.3. Правые и левые системы координат.
- •9.4. Векторное произведение двух векторов.
- •9.5. Смешанное произведение векторов.
- •10.1. Плоскость в пространстве.
- •10.1.1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
- •10.1.2.Общее уравнение плоскости.
- •10.1.3. Уравнение плоскости, проходящей через три точки.
- •10.1.4. Взаимное расположение двух плоскостей.
- •10.1.5. Угол между двумя плоскостями.
- •10.2. Прямая в пространстве.
- •10.2.1. Векторно-параметрическое уравнение прямой.
- •10.2.6. Взаимное расположение прямых в пространстве.
- •10.3. Задачи на прямую и плоскость в пространстве.
- •10.3.1. Прямая как пересечение двух плоскостей.
- •10.3.2. Взаимное расположение прямой и плоскости.
- •10.3.3. Угол между прямой и плоскостью.
- •10.3.4. Расстояние от точки до плоскости.
- •10.4. Цилиндры второго порядка.
- •10.5. Поверхности вращение второго порядка.
- •10.6. Поверхности второго порядка.
- •11.1. Линейные пространства и их простейшие свойства.
- •11.2. Линейная зависимость и независимость векторов.
- •11.3. Размерность и базис линейного пространства.
- •12.1. Понятие функции.
- •12.2. Понятие функции нескольких переменных.
- •12.3. Предел функции.
- •12.4. Односторонние пределы функции.
- •12.5. Предел функции при стремлении аргумента к бесконечности.
- •12.6. Бесконечно большие и бесконечно малые функции.
- •13.1. Основные теоремы о пределах функций.
- •13.2. Замечательные пределы.
- •14.2. Точки разрыва функции и их классификация.
- •17.1. Признак возрастания и убывания функции.
- •17.2. Экстремум функции. Необходимое и достаточное условие экстремума.
- •17.3. Направления выпуклости, точки перегиба.
- •17.4. Асимптоты.
- •17.5. Исследование функций и построение графиков.
- •18.1. Понятие о первообразной функции.
- •18.2. Неопределённый интеграл и его свойства.
- •18.3. Таблица основных неопределённых интегралов.
- •18.4 Понятие об основных методах интегрирования.
- •19.1. Задача о площади криволинейной трапеции.
- •19.2. Понятие определённого интеграла.
- •19.3. Свойства определенного интеграла.
- •19.4. Теорема об оценке определённого интеграла. Теорема о среднем.
- •19.5. Определённый интеграл с переменным верхним пределом, его свойства. Формула Ньютона-Лейбница.
- •19.6. Основные методы интегрирования.
- •19.7. Приложения определённого интеграла.
- •19.7.1. Площадь криволинейной трапеции.
- •19.7.3. Площадь поверхности вращения.
- •19.7.4. Объём тела.
- •20.1. Интегралы с бесконечными пределами.
- •20.2. Интегралы от неограниченных функций.
- •21.1. Основные понятия.
- •21.2. Предел и непрерывность.
- •21.3. Частные производные первого порядка.
- •21.4. Частные производные высших порядков.
- •21.5. Дифференцируемость полный дифференциал.
- •21.6. Экстремум функции двух переменных.
- •21.7. Метод наименьших квадратов.
- •22.1. Двойной интеграл и его свойства.
- •Вычисление двойного интеграла в прямоугольных декартовых координатах.
- •22.2. Тройной интеграл и его вычисление.
- •23.1.Основные понятия.
- •23.1.Основные свойства числовых рядов.
- •23.3. Положительные ряды.
- •23.4. Знакочередующиеся ряды.
- •23.5. Абсолютная и условная сходимость.
- •23.6. Функциональные ряды.
- •23.7. Степенные ряды.
- •24.1. Основные понятия.
- •24.2. Дифференциальные уравнения первого порядка.
- •25.2. Случаи понижения порядка.
- •25.3. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •25.3.1. Линейное однородное ду второго порядка с постоянными коэффициентами имеет вид
- •25.3.2. Линейное неоднородное ду второго порядка с постоянными коэффициентами имеет вид
20.1. Интегралы с бесконечными пределами.
Пусть
функция
![]() непрерывна при любом
непрерывна при любом
![]() .
Рассмотрим определённый интеграл с
переменным верхним пределом
.
Рассмотрим определённый интеграл с
переменным верхним пределом
![]() .
.
Предположим,
что при
![]() функция
функция
![]() имеет конечный предел; этот предел
называется сходящимся
несобственным интегралом от
функции
по промежутку
имеет конечный предел; этот предел
называется сходящимся
несобственным интегралом от
функции
по промежутку
![]() и обозначается
и обозначается
![]()
![]()
![]() .
.
Если же этот предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.
Геометрически
несобственный интеграл от неотрицательной
функции выражает площадь бесконечной
криволинейной трапеции, ограниченной
сверху графиком функции
,
слева
прямой
![]() ,
снизу
осью
(В
случае сходящегося интеграла эта площадь
является конечной, в случае расходящегося
бесконечной) (Рис.20.1.).
,
снизу
осью
(В
случае сходящегося интеграла эта площадь
является конечной, в случае расходящегося
бесконечной) (Рис.20.1.).
Е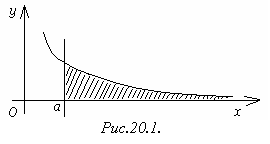 сли
сли
![]()
первообразная для
,
то
первообразная для
,
то
=
![]() =
=
=
![]() ,
где
,
где
![]() =
=
![]() .
.
и несобственный интеграл с обоими бесконечными пределам
![]()
![]() и несобственный
интеграл с обоими бесконечными пределами
и несобственный
интеграл с обоими бесконечными пределами
![]()
![]() +
+![]() ,
где с
любая точка из интервала
,
где с
любая точка из интервала
![]() .
.
С помощью следующих двух теорем можно исследовать вопрос о сходимости некоторых несобственных интегралов.
Теорема
1. Если при
выполнены неравенства
![]() и
и
![]() сходится, то сходится и
сходится, то сходится и
![]() ,
причём
,
причём
;
если же расходится, то расходится и интеграл .
Теорема
2. Если в
промежутке
![]() функция
меняет знак и
функция
меняет знак и
![]() сходится, то сходится также
.
сходится, то сходится также
.
20.2. Интегралы от неограниченных функций.
Если
функция
не ограничена в окрестности точки с
отрезка
и непрерывна при
![]() и
и
![]() ,
то несобственный интеграл от этой
функции определяется формулой
,
то несобственный интеграл от этой
функции определяется формулой
=
![]()
![]() +
+![]()
![]() ,
где
,
где
![]() (1)
(1)
В
случае, когда
![]() или
или
![]() ,
получаем
,
получаем
=
![]() (2)
(2)
=
![]() (3)
(3)
Несобственный интеграл (2) или (3) называется сходящимся, если существует конечный предел соответствующего определённого интеграла; в противном случае интеграл называется расходящимся. Несобственный интеграл (1) называется сходящимся, если существует и конечны оба предела в правой части.
Для интегралов от неограниченных функций справедливы теоремы, аналогичные теоремам 1 и 2.
21.1. Основные понятия.
Определение.
Пусть имеется n
переменных величин, и каждому набору
их значений (![]() )
из некоторого множества X
соответствует одно вполне определённое
значение переменной величины z.
Тогда говорят, что задана функция
нескольких переменных z
=
)
из некоторого множества X
соответствует одно вполне определённое
значение переменной величины z.
Тогда говорят, что задана функция
нескольких переменных z
=
![]() (
).
(
).
Пример.
Формула V
=
![]() R2H
задаёт объём цилиндра V
как функцию двух переменных V(R;H),
где R
− радиус основания, H
− высота цилиндра.
R2H
задаёт объём цилиндра V
как функцию двух переменных V(R;H),
где R
− радиус основания, H
− высота цилиндра.
Переменные называются независимыми переменными или аргументами, z зависимой переменной, а символ означает закон соответствия. Множество X называется область определения функции.
Рассмотрим некоторые примеры функции нескольких переменных:
Функция z =
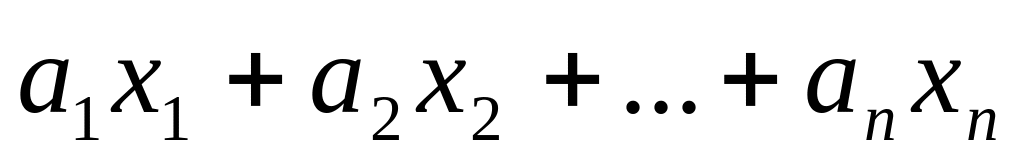 ,
где
,
где
 ,
− постоянные числа, называется линейной.
,
− постоянные числа, называется линейной.Функция z =
 ,
где
,
где
 −
постоянные числа, называется
квадратической.
−
постоянные числа, называется
квадратической.Одно из базовых понятий экономической теории − функция полезности. Эта функция z = ( ), выражающая полезность от n приобретённых товаров . Чаще всего встречаются следующие её виды:
а) z
=
![]() ,
где
,
где
![]() ,
,
![]() ,
− логарифмическая
функция;
,
− логарифмическая
функция;
б) z
=
![]() ,
где
,
,
где
,
![]() ,
− функция
,
− функция
постоянной эластичности.
Также часто в экономике встречается понятие производственной функции, выражающей результат производственной деятельности от обусловивших его факторов. Например, при n = 2 для величины общественного продукта z =
 ,
где
,
где
 − затраты труда,
− затраты труда,
 −
объём производственных фондов,
−
объём производственных фондов,
 −
постоянные числа.
−
постоянные числа.
В дальнейшем будем вести изложение для функции двух переменных (n= 2). При этом, практически все понятия и теоремы, сформулированные для n =2, легко переносятся и на случай n > 2 кроме того, рассмотрения двух переменных позволяет использовать наглядную иллюстрацию.
