Тема10 питання 2. Види,методи формування вибірок.
Види відбору: 1)Індивідуальний- коли у вибірок сукупність відбираються окремі одиниці генеральної сукупності. 2)Груповий- коли відбираються групи одиниць.
3) Комбінований –комбінування групового та індивідуального відборів.
Метод відбору- це визначена можливість продовження участі одиниці , що вже була відібрана,у подальшій процедурі відбору.
Метод відбору: 1)повторний відбір- одиниця ,що потрапила у вибірку після реєстрації досліджуваних ознак повертається назад у генеральну сукупність для участі і подальшій процедурі відбору. 2) без повторний відбір –одиниця,що потрапила до вибірки не повертається до генеральної сукупності, подальший відбір відбувається без неї.
При
достатньому обсязі вибірок сукупності
n
ймовірність того ,що похибки вибірки
∆, не перевищує свого граничного значення
∆=tμ
, за теорії Ляпунова інтегралу Лапласа:
P(∆≤tμ)=
μ –це середньоквадратична або стандартна
похибка вибірки. t-
це
довірче число для заданого значення
ймовірності Р , яке визначається за
табличного значенн функції
Згідно таблиці значень функції : t=1 це P(∆≤μ)= 0,683. t=2 це P(∆≤2μ)=0,954. t=3 це P(∆≤3μ)=0,9973. t=4 це P(∆≤4μ)=0,99993.
Наведені дані вказують на те,що практично неймовірно отримати похибку вибірки > ніж 3μ.
Стандартна похибка вибірки μ є середнім квадратичним відхиленням вибіркових точкових вибірок: вибіркова середня ͠х ,або вибіркової частки ω від значень відповідних параметрів генеральної сукупності.
-при
повторному відборі μ=
–при без повторному відборі μ=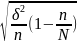
.
де
-вибіркова
дисперсія ,
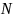-відповідно обсяг вибіркової та
генеральної сукупностей.
При
практичному використанні наведених
формул слід враховувати ,що:
-
дисперсія
частки є добутком часток.
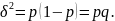
У
великих за обсягом вибіркових сукупностях
( n≥30)
поправка
не
вносить істотних змін у розрахунки , а
тому враховується лише в малих вибірках.
μ=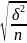
.
Коригуючих
множин для без повторної вибірки при
малих величинах
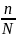наближається до 1 ,а тому при 1…5%-ій
вибірці (
=0,01…0,05)
розрахунок μ ведеться за формулою для
повторної вибірки.
Гранична похибка вибірки (∆≤tμ) –це максимально можлива похибка для прийнятої ймовірності Р.
Довірне
число
t
вказує,як
співвідноситься гранична та стандартна
похибки . Отже, розмір граничної похибки
середньої величини і частки обчислюється
обчислюється за такими формулами для
відбору :
- повторного
,
.
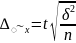-безповторного
=
,
=
.
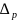Як видно з формул розмір граничної похибки залежить від варіації ознаки в генеральній сукупності D (дисперсії),яку приймають рівною вибірковій ,обсяг вибірки n та її частки у генеральній сукупності , а також прийнятого рівня ймовірності, якому відповідає квантиль.
Виходячи з того ,що гранична похибка вибірки для ймовірності Р ,є максимальним відхиленням розміру значень вибіркової оцінки від характеристик генеральної сукупності,можливі межі значень останньої визначають так:
-для
середньої величини ͞х=͠ х
,-для частки W=ω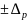
.
,де х-значення середньої величини ознаки відповідно генеральній і вибірковій сукупностей. р і ω- частки елементів відповідно.