1.2. Декартова (правая) система координат

Напомним, что в правой системе за положительное принимается направление отсчета углов (поворотов) против часовой стрелки. Радиус-вектор точки как функция времени задается тремя координатами , являющимися также функциями времени. Вводя единичные векторы вдоль осей Ox, Оу, Oz соответственно, представим в виде

. (3.1)

Функции - компоненты радиус-вектора, т. е. декартовы координаты точки.

Дифференцируя (3.1) по времени с учетом равенств , получим разложение вектора скорости точки по ортам декартовой системы координат:

. (4.1)

И аналогично получим вектор ускорения точки:

. (5.1)

Для справочных целей напомним следующее представление вектора :

, (6.1)

где - компоненты секторной скорости вдоль декартовых осей.

1.3. Цилиндрическая система координат

Положение точки в пространстве в момент времени можно определить тройкой величин , которые являются цилиндрическими координатами точки (рис. 2.1). Формулы преобразования от декартовых координат к цилиндрическим и обратно имеют вид

, (7.1)

. (8.1)

Это так называемые точечные преобразования; формулы этих преобразований содержат только координаты («старые» и «новые»), но не содержат явным образом временной переменной. Последнее означает, что обе системы координат описывают движение точки в одной и той же (неподвижной) системе отсчета. Области изменения цилиндрических координат: .

Координатные поверхности в цилиндрической системе²: - семейство цилиндров кругового сечения радиуса с осью Оz; - семейство полуплоскостей, исходящих из оси Оz , в которых лежат радиус-вектор точки и ось Оz; - семейство плоскостей, перпендикулярных Oz. Линия пересечения двух каких-либо координатных поверхностей различных семейств называется координатной линией. Так как вдоль каждой координатной линии меняется только одна координата, то ее и называют соответствующей координатой. Очевидно, координатные линии - это концентрические окружности, координатные линии - это полупрямые (лучи), исходящие из начала координат О (см. рис. 2.1), координатные линии - прямые, параллельные оси Oz. Так как координатные линии не являются прямыми, цилиндрические координаты относятся к криволинейным. Очевидно, что три координатные линии, которые определяют точку пространства , пересекают друг друга под прямыми углами, т. е. цилиндрические координаты являются ортогональными координатами.

Касательная, проведенная к данной точке координатной линии, называется координатной осью. Все три оси цилиндрической системы координат ортогональны друг другу. Отложим по этим осям единичные векторы в направлении возрастания координат и разложим радиус-вектор точки по ортам цилиндрических координат:

. (9.1)

Из рис. 2.1 видно, что орты цилиндрических координат связаны с ортами декартовых координат соотношениями

(10.1)

Отсюда видно, что при перемещении точки относительно S положение ортов , изменяется вследствие изменения угла . Действительно, вычислим и

(11.1)

Дифференцируя (9.1) по t и учитывая (11.1), находим разложение вектора скорости точки по ортам цилиндрической системы координат:

. (12.1)

Аналогично, дифференцируя по t и учитывая (11.1), получим

. (13.1)

Таким образом, проекции скорости и ускорения точки на координатные оси имеют вид

(14.1)

Приведем также разложение вектора секторной скорости точки по ортам цилиндрической системы координат:

(15.1)

Из (14.1) и (15(1) следует, что

. (16.1)

Рассмотрим далее важный случай движения, при котором секторная скорость точки остается постоянной, т. е. .

Введем цилиндрическую систему координат с осью Оz, направленной по вектору .

Так как , то и радиус-вектор и скорость точки в любой момент времени лежат в плоскости, ортогональной вектору . В этом случае проекции скоростей и ускорений можно непосредственно выразить как функции и , а не и , а также через производные по функции . Действительно, в выбранной системе координат имеем

(17.1)

. (18.1)

Значит,

. (19.1)

Далее из (16.1) имеем , а

(20.1)

Так что

. (21.1)

Формулы (19.1) и (21.1) называют первой и второй формулами Бине соответственно. Они оказываются полезными при исследовании различных случаев движения материальной точки в центрально-симметричном силовом поле.

Пример. Траектории точек являются плоскими и определяются уравнениями

а) , б) ,

- параметр, - эксцентриситет эллипса, секторная скорость . Начало цилиндрических координат помещено в фокусе эллипса. Определить ускорения точек.

Прежде всего, заметим, что траектории точек различны. Так, в случае а) точка движется по эллипсу (рис. 3.l, а), в то время как в случае б) траектория представляет собой розетку и не обязательно является замкнутой кривой (рис. 3.1, б).

По второй формуле Бине, дважды дифференцируя по , находим

и в случае а),

а и в случае б).

Отличие в ускорениях точек согласно уравнениям движения означает, что действующие на точки в случаях а) и б) силы имеют разные законы убывания с расстоянием от центра силы до точки. В частности, в случае б) сила ~ . Если речь идет о движении планет в гравитационном поле Солнца, то мы видим, что в случае б) перигелий планеты при каждом обороте смещается на величину .

Пример. Определение радиус-вектора точки по скорости

Определить закон движения, траекторию и ускорение точки, движущейся по плоской траектории с постоянной секторной скоростью, еcли , где - расстояние от точки до центра, , причем угол между векторами и равен .

Направим полярную ось от центра к точке так, чтобы при , тогда , а . Отсюда , так как если , то . Разделяя переменные

и интегрируя, получим

.

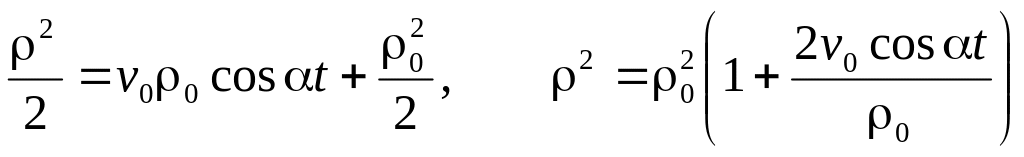Далее найдем :

.

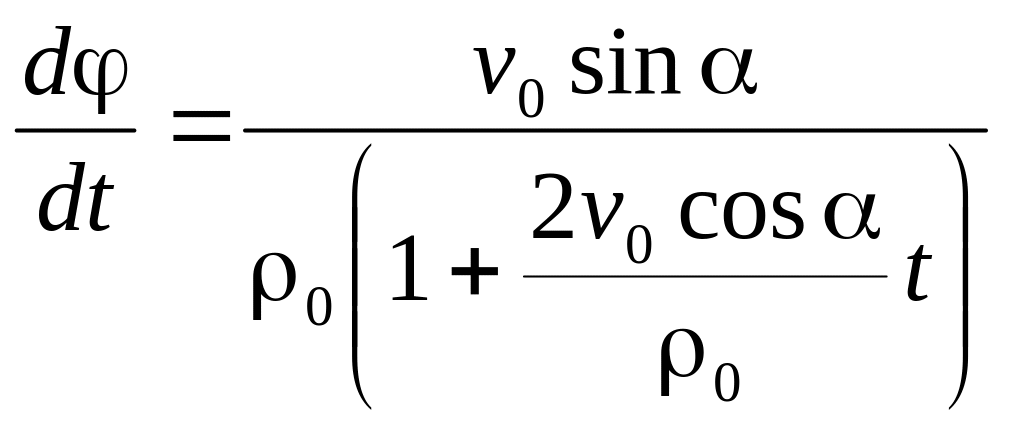Отсюда

или

.

Ускорение точки найдем по формуле Бине в виде:

.