Министерство транспорта РФ

ФГОУ ВПО НГАВТ

Кафедра водных путей, гидравлики и гидроэкологии

Курсовая работа

по дисциплине «Гидравлика»

Тема: «Гидравлический расчёт системы, состоящей из цилиндрических каналов различных поперечных сечений и дюкера»

Студент гр. ГТ-31: Зырянов К. Ф.

Преподаватель: Михайлова Т. Н.

Новосибирск 2012

СОДЕРЖАНИЕ

Введение

Построение кривой свободной поверхности представляет практический интерес и позволяет определить глубины воды в канале с постоянным уклоном дна и в каналах, трассируемых по местности с изменяющимися уклонами. Определение глубины в различных сечениях канала позволяет установить размеры затопления берегов при возведении гидротехнических сооружений и решать вопросы о креплении откосов каналов.

В курсовой работе необходимо рассчитать и построить кривую свободной поверхности потока в призматическом канале с изменяющимся уклоном дна.

Курсовая работа состоит из пояснительной записки с необходимыми расчетными таблицами, формулами и графиками, а также продольного профиля канала с нанесенными линиями дна, нормальной, критической и фактической глубин.

Схема системы состоящей из каналов трапецеидального и параболического сечений, соединенных ж/б дюкером.

b₁=2,5 м L₂=15 м n₃=0,03

n₁=0,02 α₂=20⁰ i₃=1,0∙10^-4

m₁=1,2 м ∆₂ =1,1 p₃=2,0 м

i₁=3,0∙10^-4 L₃ =3,9 км

1. Расчёт канала трапецеидального сечения

1. 1 Расчёт нормальной глубины потока

Глубина потока, соответствующая равномерному движению, называется нормальной глубиной и обозначается символом . Основной зависимостью при определении нормальной глубины в данном расчёте является:

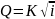, (1.1)

где – модуль расхода;

– площадь живого сечения, м²;

– гидравлический радиус, м;

- коэффициент Шези, м^0,5/с;

- уклон дна.

Для определения нормальной глубины находим модуль расхода, которым должен характеризоваться канал в случае, если в русле установится равномерное движение .

м³/с.

Задаваясь произвольной величиной , определяем расходную характеристику при этой глубине. Если найденное значение отклоняется от не более чем на 5%, то глубину можно считать равной искомой глубине потока . Рассчитывается отклонение по формуле (1.2). В противном случае следует задаться новой глубиной и проверку модуля расхода .

(1.2)

Таблица 1.1 Расчет нормальной глубины потока

Величина или расчётная формула	Единица измерения	Численные значения
0	м	1,15
	м2	4,46
	м	6,09
	м	0,73
	м0,5/с	47,47
	м3/с	181,26

м³/с м³/с.

Принимаем нормальную глубину потока м.

1. 2 Расчёт критической глубины

Критической глубиной ( ) называется глубина, отвечающая минимуму удельной энергии сечения.

Определяем критическую глубину, используя уравнение критического состояния

, (1.3)

где и - соответственно площадь живого сечения и ширина потока поверху, отвечающие критической глубине .

Величина является постоянной и её вычисляем по известному расходу , при .

м⁵.

Расчёт ведём в табличной форме (таблица 1.2).

Таблица 1.2 – расчет критической глубины потока

Величина или расчётная формула	Единица измерения	Численные значения
к	м	0,5
	м	3,7
	м2	1,55
	м5	1,00

Проверяем не превышает более чем на 5 % велечину по формуле:

(1.4)

.

Принимаем критическую глубину м.