
7. Расход. Уравнение расхода.
Расход - это количество жидкости, которое протекает через данное сечение в единицу времени. Количество жидкости можно измерять в единицах объема, массы или веса, в связи c чем различают объемный Q (м3/с), массовый Qm (кг/c) и весовой QG (Н/c) расходы. Между этими расходами существует такая же связь, как между объемом, массой и весом, т.е.
Qm = Q ∙ ρ ; QG = Q ∙ ρ ∙g ; QG = Qm ∙ g .
Расход
связан со скоростью жидкости
![]() и площадью поперечного сечения S
струйки
или потока зависимостью
и площадью поперечного сечения S
струйки
или потока зависимостью
![]() (14)
(14)
Следует
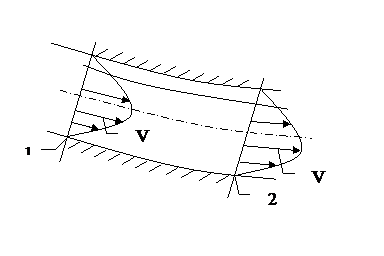
отметить, что при течении реальной
(вязкой) жидкости, из-за трения между ее
слоями, скорости переменны по сечению
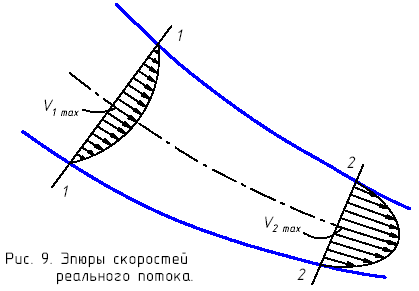
потока (рис.9). B этом случае, скорость,
удовлетворяющую условию (14) называют
средней (![]() ).
Очевидно, что она лежит в пределах
от
=
0 до
=
).
Очевидно, что она лежит в пределах
от
=
0 до
=![]() .
.
Уравнение расходов представляет собой равенство расходов в двух сечениях потока (рис.9), т.е.
Q1 = Q2
или, с учетом (14),
![]()
 ,
(15)
,
(15)
где и S - средняя скорость и площадь соответствующего сечения.
Используя зависимость (15) можно найти среднюю скорость в любом сечении потока жидкости, если в каком-то сечении этого потока скорость уже известна и известны его геометрические размеры.
Уравнение расхода является законом сохранения массы для движущейся жидкости.
8. Уравнение неразрывности жидкости Довольно часто при решении задач приходится определять неизвестные функции типа:
1) р
= р (х, у, z,
t) –
давление;2) nx(х,
у, z,
t),
ny(х,
у, z,
t),
nz(х,
у, z,
t) –
проекции скорости на оси координат х,
у, z;3) ρ
(х, у, z,
t) –
плотность жидкости.Эти неизвестные,
всего их пять, определяют по системе
уравнений Эйлера.Количество уравнений
Эйлера всего три, а неизвестных, как
видим, пять. Не хватает еще двух уравнений
для того, чтобы определить эти неизвестные.
Уравнение неразрывности является одним
из двух недостающих уравнений. В качестве
пятого уравнения используют уравнение
состояния сплошной среды.![]() Формула
(1) является уравнением неразрывности,
то есть искомое уравнение для общего
случая. В случае несжимаемости жидкости
∂ρ/dt
= 0, поскольку ρ
= const,
поэтому из (1) следует:
Формула
(1) является уравнением неразрывности,
то есть искомое уравнение для общего
случая. В случае несжимаемости жидкости
∂ρ/dt
= 0, поскольку ρ
= const,
поэтому из (1) следует:![]() поскольку
эти слагаемые, как известно из курса
высшей математики, являются скоростью
изменения длины единичного вектора по
одному из направлений X,
Y,
Z.Что
касается всей суммы в (2), то она выражает
скорость относительного изменения
объема dV.Это
объемное изменение называют пооразному:
объемным расширением, дивергенцией,
расхождением вектора скоростей.Для
струйки уравнение будет иметь вид:
поскольку
эти слагаемые, как известно из курса
высшей математики, являются скоростью
изменения длины единичного вектора по
одному из направлений X,
Y,
Z.Что
касается всей суммы в (2), то она выражает
скорость относительного изменения
объема dV.Это
объемное изменение называют пооразному:
объемным расширением, дивергенцией,
расхождением вектора скоростей.Для
струйки уравнение будет иметь вид:![]() где
Q
– количество жидкости (расход);ω–
угловая скорость струйки;∂l
– длина элементарного участка
рассматриваемой струйки.Если давление
установившееся или площадь живого
сечения ω
= const,
то ∂ω
/∂t
= 0, т. е.
согласно (3),ρ∂Q/∂l
= 0, следовательно,
где
Q
– количество жидкости (расход);ω–
угловая скорость струйки;∂l
– длина элементарного участка
рассматриваемой струйки.Если давление
установившееся или площадь живого
сечения ω
= const,
то ∂ω
/∂t
= 0, т. е.
согласно (3),ρ∂Q/∂l
= 0, следовательно,![]()
Уравнение Бернулли для струйки идеальной жидкости
Рассмотрим установившееся течение жидкости, находящейся под воздействием только одной массовой силы - веса жидкости.
Выделим
в потоке струйку, такую малую, что
изменением параметров в ее поперечном
сечении можно пренебречь и считать
их постоянными.За бесконечно малый
промежуток времени Dt
участок струйки 1-
2
переместится
в положение 1?-
2?.
Применим к этой струйке уравнение
энергии, заключающееся в том, что
работа сил по перемещению струйки
равна приросту кинетической энергии
этой струйки.Известно, что элементарная
работа силы определяется выражением
Т.
к. в первом сечении направление сил
давления совпадает с направлением
вектора скорости, а во втором сечении
оно противоположно, то
Заметим,
что работа сил давления, действующих
по боковым поверхностям струйки равна
0, вследствие ортогональности векторов
давления и скорости.Суммарная работа
поверхностных сил определится
выражением
Т.
к. приток массы в рассматриваемой
струйке отсутствует, то
M1
= M2
следовательно
W1
= W2
Нетрудно
заметить, что объем 1?-2 для рассматриваемых
положений является общим, тогда
Применяя
такой же прием, получим выражение для
прироста кинетической энергии
струйки
после
преобразований, с учетом того, что dW1
= dW2
=dW
=dG/g,
получаем
Рис. 3.2 Таким образом, согласно уравнению Бернулли, полный напор представляет собой сумму гидростатического и скоростного напора и для выделенной струйки жидкости это величина постоянная. Проиллюстрируем это положение графиком, см. рис. 3.2. |
Уравнение Бернулли для реальной вязкой жидкости
Рис. 3.3
Будем
считать, что по всему поперечному
сечению
Выделим в общем потоке элементарную струйку, такую тонкую, что изменением параметров в поперечном сечении будем пренебрегать. От трубки к трубке параметры потока будем считать переменными.
Введем
понятие элементарной мощности потока,
которая переносится элементарной
струйкой dN.
Известно,
что
Подставляя
в (3.1), получим
Экспериментально
установлено
следующее:
развернутая
форма уравнения Бернулли:
|

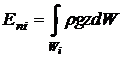 Учитывая,
что для несжимаемой жидкости r=
const,
получим
Учитывая,
что для несжимаемой жидкости r=
const,
получим
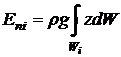 Объем,
занимаемый струйкой в начальном и
конечном положениях можно представить
в виде двух составляющих, рис. 3.1.
Объем,
занимаемый струйкой в начальном и
конечном положениях можно представить
в виде двух составляющих, рис. 3.1.
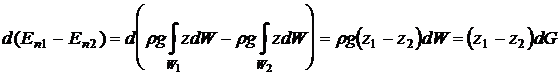 где
dG
= rgdW
- элементарный вес жидкости, заключенный
в объеме dW.
Т.
е.
где
dG
= rgdW
- элементарный вес жидкости, заключенный
в объеме dW.
Т.
е.
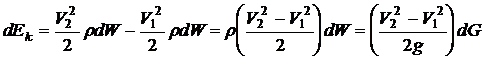 Запишем
уравнение баланса энергии
Запишем
уравнение баланса энергии
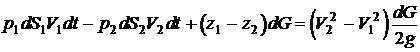
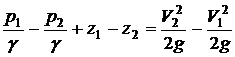 или,
после перегруппирования членов
или,
после перегруппирования членов
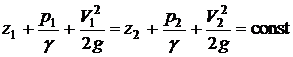 Это
выражение и представляет собой
уравнение Бернулли для идеальной
несжимаемой жидкости.
Величина
Это
выражение и представляет собой
уравнение Бернулли для идеальной
несжимаемой жидкости.
Величина
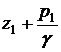 определена
ранее как гидростатический напор, а
величина
определена
ранее как гидростатический напор, а
величина
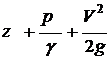 получила
название полный напор.
получила
название полный напор.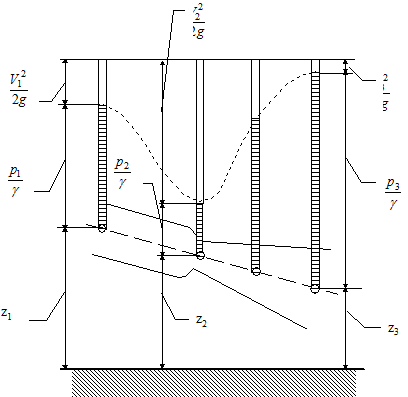
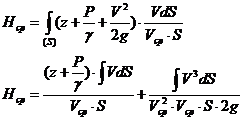
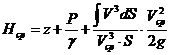 (3.2)
(3.2)
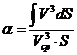 - коэффициент неравномерности потока.
(3.3)
- коэффициент неравномерности потока.
(3.3)